线段树 从零开始的入门到提高十分钟包会教程

恭喜你找到了这篇博客！虽然这个标题看起来非常像是nc营销号的标题但是！请相信我一次这是真的！如果不行请随时取关！等等你好像还没关注我那不如现在先关注看完再取关吧哈哈

首先我们先明确两件事情！

1. 线段树他是个树！
2. 线段树是基于一个数组生成的！

好的这就已经大概勾勒出线段树美丽的轮廓了！那我们先来看一张照片。其中树的部分已经用看起来非常像树的颜色涂好了。

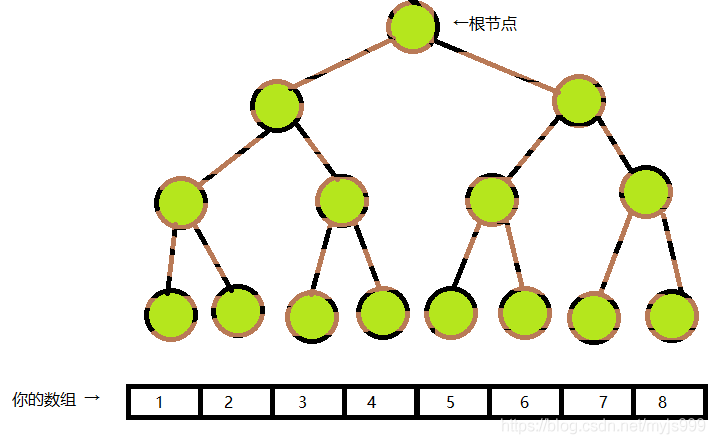
好那么废话不多讲我们就来说这个树是怎么长出来的吧。

我们要知道的是，树的每个节点上记录了一个区间。比如说，根节点记录了区间$[1,8]$，刚好是整个数组的长度。那么其他节点呢？这就是线段树的巧妙之处了。一个节点有两个子节点，且它们平分自己的区间。因此，根节点的两个子节点就分别对应了$[1,4]$和$[5,8]$。接下来$[1,4]$这个节点的两个子节点就是$[1,2]$和$[3,4]$。

标上的每个节点代表的区间的照片如下。

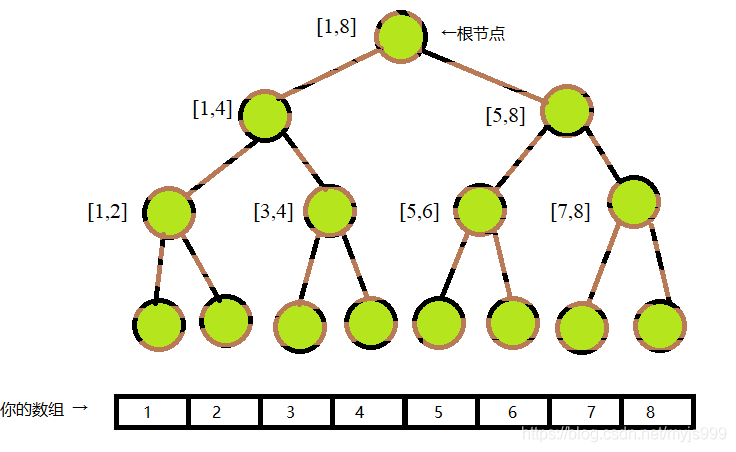
最下面那一排为什么没有标呢？因为叶子节点刚好对应一个长度为$1$的区间，即从左到右分别为$[1,1],[2,2],\cdots ,[8,8]$。显然它也不会有儿子了。

哦我的天，你已经学会怎么基于数组建立线段树了！我相信到现在你应该还没用到$2$分钟吧！

（其中看废话还要占$1$分钟）

还有一个小细节，比如假设你有一个区间$[1,3]$它的长度是奇数这时怎么平分呢？其实左右那边长一点都没有关系，因此放心用你的整除号就行了。

现在我们来看看线段树能干些什么吧_(¦3」∠)_

求区间最大值——用线段树节点表示指定区间

假设数组上的每个位置有一个数，如何求一段区间里的数的最大值呢？

枚举每个位置？时间复杂度$O(L)$太高了不能接受（$L$表示区间长度）。考虑用我们刚学的线段树来解决这个问题。

你有没有发现一个节点所代表的区间的最大值就是其子节点代表的区间的最大值的最大值？比如说$[1,4]$的最大值就是【$[1,2]$的最大值】与【$[3,4]$的最大值】这两个值取最大值。啊你可能说这不是废话吗。那我们放到线段树里面看看呢？比如说我们要求$[2,7]$这个区间的最大值。

假设我们在每个节点记录其所代表的区间的最大值。为了方便叙述，就把这个值叫做这个节点的maxnum吧。

那么$[2,7]$的最大值也就是节点$[2,2]$、$[3,3]$、……、$[7,7]$这些节点的maxnum的最大值。根据我们图片前面那段字提到的，这些节点求最大值等于——

$[2,2],[3,4],[5,6],[7,7]$四个节点求最大值。

哦我的天哪！原来我们要查$6$个节点的最大值，现在只用查$4$个了！在时间复杂度上这个优化看起来更明显——这样求区间最大值的时间复杂度是$O({\log }_{2}L)$的（L是区间长度）。

再来一次，求区间$[4,8]$的最大值最少要查几个线段树节点呢？答案是1-1+4-5-1+4个。

那么我们如何实现这一神奇的过程呢？用一个简单的DFS（深度优先搜索）即可。搜索时记录两个值templeft和tempright，表示当前考虑的区间，它一定是某个节点所代表的区间。最开始调用DFS(1,N)，其中N是数组长度。函数内流程如下：

1.先判断[templeft, tempright]是不是含于要查的区间。如果是的话，那么如之前所说，我们就没有必要再查它的子节点了，此时返回这个区间的maxnum值并退出。否则继续。

2.现在我们知道了我们这个区间是这样的。

或者是这样的。

为什么红框框不会全然在黑框框在外面呢？马上就知道了。

我们求出temp区间的两个子节点的区间，分别判断一下是不是全然在黑框框外面，如果是的话就PASS，否则就递归。这样递归的结果要么是全然含于黑框框（在Case1就结束），要么又是一只脚在里面一只脚在外面。

int query_max(node* tempnode, int templeft, int tempright) { // tempnode表示当前查到的节点 
	if(aimleft <= templeft && aimright >= tempright) { // 完全包含 
		return tempnode->maxnum;
	}
	int middle = (templeft + tempright) / 2;
	int tempanswer = -1; // 初始化为极小值，假设存的数都是非负数
	if(aimleft <= middle) {
		int leftanswer = query_max(tempnode->leftchild, templeft, middle);
		tempanswer = max(tempanswer, leftanswer);
	}
	if(aimright >= middle + 1) {
		int rightanswer = query_max(tempnode->rightchild, middle + 1, tempright);
		tempanswer = max(tempanswer, rightanswer);
	}
	return tempanswer;
}

哦讲完啦O(∩_∩)O ！！

什么？你已经看了十分钟了Σ(⊙▽⊙？？

那你真是太走运了！因为线段树的所有难点现在已经全 數 攻 破了。从此以后，这篇博客只有废话，再无难点……所以不如再看五分钟？(╹▽╹)

修改某位置的值同时查询区间——维护线段树

维护这个词就非常的生动形象啦。比如$[3,3]$上的值变了，what will happen?

很明显呢，包含$[3,3]$这个区间的区间，它们的值都有可能改变。在线段树上这些节点就是树上的一根树枝丫丫，所以挨个修改这些节点就好了。时间复杂度同样也是$O({\log }_{2}N)$的（N是数组长度）。

实现也很简单，就用上面的实现，目标区间就设为$[p,p]$吧……（p是修改的位置）。因为黑框框现在是个黑点点了，所以所有情况就都是Case1了。把DFS经过的节点的maxnum都改改就行了。

void modify(node* tempnode, int templeft, int tempright) {
	if(templeft == tempright) { // 目标点（叶子结点） 
		tempnode->maxnum = aimnum;
		return;
	}
	int middle = (templeft + tempright) / 2;
	if(aimp <= middle) modify(tempnode->leftchild, templeft, middle);
	else modify(tempnode->rightchild, middle+1, tempright);
	tempnode->maxnum = max(tempnode->leftchild->maxnum, tempnode->rightchild->maxnum); // 回溯时更新
}

修改区间——懒标记

终于，到了考验博主和读者水平的时刻了。如果你只是想稍微了解一下线段树，恭喜你，你已经超过80%的网上看了半天还是连线段树是什么都不知道的人了。如果你真的想学透线段树的话，还是耐心看看下面这些内容吧。博主将尽量用最易懂的方法，让读者用最短的时间、花最少的精力学会并精通一样算法。所以请静下心来看看吧。

……

啊☆(>w<)这个读者好认真！我都忍不住想打住吹水的欲望了呢！

我们还是考虑假设要修改区间$[2,7]$，我们知道，它实际上对应的区间就是那$4$个区间。因此我们找到这$4$个区间并修改它们。

而且我们要维护这个线段树，因此每个红色点到根节点的树枝都要修改。

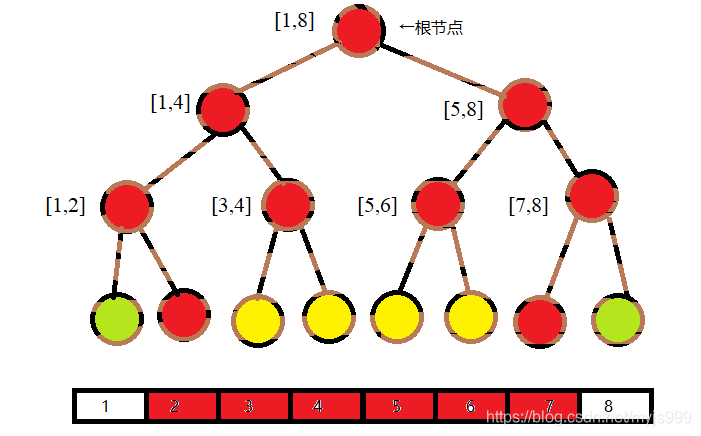
看起来没什么问题……但如果我们查一下区间$[4,4]$呢？

他居然没有被改到！

难不成要把黄色节点也改了？

哦我的天呐，看这红彤彤的树，想都不用想时间复杂度已经炸飞了……

还是回到上一幅图。

虽然我们修改操作只能做到这样了，但是我们能不能在查询的时候上下其手呢？

比如说，我们能不能在查到$[3,4]$这个区间并且发现要继续往下走的时候，才把$[3,4]$的子节点涂红呢？

有人说那你这和刚才那个鬼红树有什么区别？但我们冷静分析一波，我们只是在查区间的时候附加了一个【涂子节点】的操作，这个操作是$O(1)$的，因此现在的时间复杂度和原来的是一样的！

好！我们找到了突破口！也就是说这个修改操作他非常的懒，改的时候不动，查的时候才挪一个位置……

就是一个懒标记。

现在是修改完之后的情况。那些红得发紫的节点就是有懒标记的节点。而普通的红节点，很显然，它们的儿子已经被修改了，所以不需要懒标记了。

那么查询的时候发生了什么事呢？首先我们检查这个节点上面有没有懒标记，如果有的话，我们不仅要修改他的儿子们，而且要把懒标记下推给儿子。看图就很容易理解了：

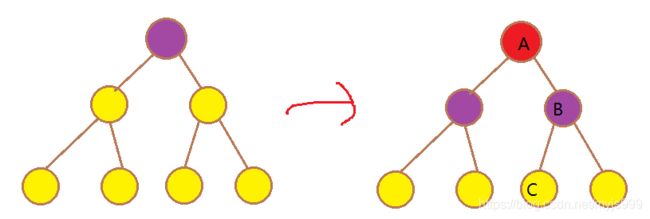
懒标记很懒，每次只会挪一步。假设我们这次的目标区间落在B上面，那么C也就不需要改了。否则的话，我们也留到DFS到B的时候再下推B的懒标记。

同时要记得把原来节点的懒标记清掉。也再说一遍，不要只下推忘了修改儿子的值，那就白 推 了。

另外，由于修改的时候也需要知道实时的值，因此修改时也要一并把标记推了。方法完全相同。

//注意：初始化时把所有lazy设为极小值 
void pushlazy(node* tempnode) {
	if(tempnode->lazy != -1) { // 有懒标记 
		tempnode->leftchild->lazy = max(tempnode->leftchild->lazy, tempnode->lazy); // 和原来的标记合并
		tempnode->rightchild->lazy = max(tempnode->rightchild->lazy, tempnode->lazy);
		tempnode->leftchild->maxnum = max(tempnode->leftchild->maxnum, tempnode->lazy);
		tempnode->rightchild->maxnum = max(tempnode->rightchild->maxnum, tempnode->lazy);
		tempnode->lazy = -1; // 清标记 
	}
}
void modify2(node* tempnode, int templeft, int tempright) {
	if(aimleft <= templeft && aimright >= tempright) { // 是红得发紫的节点 
		tempnode->maxnum = aimnum;
		tempnode->lazy = aimnum;
		return;
	}
	int middle = (templeft + tempright) / 2;
	pushlazy(tempnode);
	if(aimleft <= middle) modify2(tempnode->leftchild, templeft, middle);
	if(aimright >= middle + 1) modify2(tempnode->rightchild, middle + 1, tempright);
	tempnode->maxnum = max(tempnode->leftchild->maxnum, tempnode->rightchild->maxnum);
}
int query_max2(node* tempnode, int templeft, int tempright) { 
	if(aimleft <= templeft && aimright >= tempright) { 
		return tempnode->maxnum;
	}
	int middle = (templeft + tempright) / 2;
	pushlazy(tempnode);
	int tempanswer = -1; 
	if(aimleft <= middle) {
		int leftanswer = query_max2(tempnode->leftchild, templeft, middle);
		tempanswer = max(tempanswer, leftanswer);
	}
	if(aimright >= middle + 1) {
		int rightanswer = query_max2(tempnode->rightchild, middle + 1, tempright);
		tempanswer = max(tempanswer, rightanswer);
	}
	return tempanswer;
}

完结撒花。

举一反三

现在我们已经会区间修改，区间查询了。

但我们学的是最大值啊，求和能做吗？

wdnmd你把上面的“最大值”字样全部替换成“和”就行了。

那求个众数呢？

emmmm

有两堆数，告诉你每堆的众数，你能求出合起来的众数?？？

反过来说，只要你能求，那么线段树就能维护。

这个性质称为信息的可加性。

因此我们线段树还能维护乘积、平方和、最大公因数等等。

真·完结撒花~~

---

myjs999版权所有，禁止转载