不得不背下长长的线段树？树状数组让世界清静！
【来源】
引用自Chanis的洛谷博客。
【背景】
大家学了线段树与树状数组后，一定会觉得树状数组比线段树好写（背）多了，常数也小多了（分析lowbit操作，每次操作中每个节点被访问的概率是1/2,所以常数是1/2）但是美中不足的是树状数组不能区间修改+区间查询啊。事实上，树状数组可以做到这些，还可以查询第k大（小）值。
【单点修改，区间查询】
这种easy的东西就不多说了，贴代码。
long long sum(long long x){
long long ret=0;
while (x>0) {
ret+=c[x];
x-=lowbit(x);
}
return ret;
}
void add(long long x,long long d){
while (x<=n) {
c[x]+=d;
x+=lowbit(x);
}
}【区间修改，单点查询】
维护差分数组
，于是有
，
被表示成了一堆连续元素之和，查询操作也就很简单了。而修改操作呢，对于每一个
，我们修改差分数组，即
。程序就是上面的sum和add操作不动，主程序这么写：
scanf("%d%d",&n,&m);
memset(a,0,sizeof(a));
for (int i=1;i<=n;i++) { scanf("%d",&x);add(i,x);add(i+1,-x); }
for (int i=1;i<=m;i++) {
scanf("%d",&t);
if (t==1) {//区间[x,y]+=k
scanf("%d%d%d",&x,&y,&k);
add(x,k);add(y+1,-k);
}
else {//查询第x个数
scanf("%d",&x);
printf("%d\n",sum(x));
}
}【区间修改，区间查询】
仍然引入新数组（不是差分了窝，可以近似看成后缀）
表示区间![[i...n]](http://img.e-com-net.com/image/info8/be9978fffff1403bb92e8e213e5e9944.gif){kind=small}
要加上的值之和，于是对于每一个
，仍然可以。对于区间求和，不妨令
表示
，则有
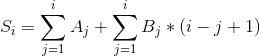，即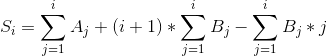
。于是代码就很显然了，用一个asum数组维护a数组的前缀和，delta1与delta2两个树状数组，delta1维护B数组的和，delta2维护
的和。
void add(int *arr int pos,int x){
while(pos<=n) arr[pos]+=x,pos+=lowbit(pos);
}
void modify(int l,int r,int x){
add(d1,l,x),add(d1,r+1,-x),add(d2,l,x*l),add(d2,r+1,-x*(r+1));
}
int getsum(int *arr,int pos){
int sum=0;
while(pos) sum+=arr[pos],pos-=lowbit(pos);
return sum;
}
int query(int l,int r){
return asum[r]+r*getsum(d1,r)-getsum(d2,r)-(asum[l-1]+l*getsum(d1,l-1)-getsum(d2,l-1));
}【区间最值】
最值是吧，来愉快地建个树：
void build(){
for(int i=1;i<=n;i++){
cin>>a[i];int pos=i;
while(pos<=n) c[pos]=max(c[pos],a[i]),pos+=lowbit(pos);
}
}
是不是很轻松的完成了？恭喜你——你没有写对。
实际上这段建树过程本身没有问题，不能说是错误的，只能说不对。。。
显然区间最值不满足区间减法，这样写每次查询都要初始化，复杂度恐怖。
换个写法：
void build(int n){
for(int i=1;i<=n;i++){
c[i]=a[i],int t=lowbit(i);
for(int j=1;j现在更新完某个数，之前的元素的值都是正确的了，显而易见，建树的时间复杂度是O(n log n)的。那么我们该如何修改呢？当然不能在父亲节点上直接修改啦（手动滑稽），换了一种建树的方式就是为了维护c数组的正确性，修改同样也要保证c数组的正确性，那么在更新父亲节点时，我们就需要查询它所有的儿子节点，代码如下：
void add(int pos,int x){
a[pos]=x;
while(pos<=n){
c[pos]=a[pos];int t=lowbit(i);
for(int j=1;j不难发现，每层循环都是lowbit操作，时间复杂度为O（王逸松）O（log(n)*log(n)),其实也没多慢，当n=1e5时，logn约等于16,就把一个logn当成常数看，线段树常数也挺大的啊，树状数组代码量还这么少。
修改是修改完了，那么问题来了，我们该如何查询？
假设当前查询的区间是[l,r]，那么我们从r到l对每一个c数组的元素所控制的叶子节点进行判断。假设现在进行到了第i项，那么显然易得（看图）：该数控制的a数组的元素是 [i-lowbit(i)+1,i]。设L=i-lowbit(i)+1,R=i。如果l<=L<=r那么就将c[L]加入最值的判断中，接着L--……，否则的话就只对第R个元素加入，然后R--……，代码如下：
int query(int l,int r){
int ans=a[r];
while(1){
ans=max(ans,num[r]); if(r==l) break; r--;
while(r-l>=lowbit(r)) ans=max(ans,c[r]),r-=lowbit(r);
//while条件里面的 r-l怎么不写成r-l+1？这才是元素个数啊。
//写r-l+1可能会跳到0，某位大佬试了一下，电脑蓝屏了。
//我也没有试，刨根问底（想要作死）的同学可以自己试一下
}
return ans;
}显然，时间复杂度是O(log n*log n)的。
完整代码如下：
void build(int n){
for(int i=1;i<=n;i++){
c[i]=a[i],int t=lowbit(i);
for(int j=1;j=lowbit(r)) ans=max(ans,c[r]),r-=lowbit(r);
}
return ans;
} 到此结束了？虽然我很想结束但是毒瘤出题人松松松似乎不会结束。。。显然他会把一维树状数组拓展到二维。
【单点修改，区间查询】
没啥好说的，上代码。
void add(int x,int y,int z){
int t=y;//注意这里需要使用一个变量保存y的值
while(x<=n){
y=t;
while(y<=n) c[x][y]+=z,y+=lowbit(y);
x+=lowbit(x);
}
}
int getsum(int x,int y){
int ans=0,t=y;
while(x){
y=t;
while(y) ans+=c[x][y],y-=lowbit(y);
x-=lowbit(x);
}
return ans;
}【区间修改，单点查询】
先考虑二维前缀和怎么做。
和一维的一样，开一个差分数组
，其他的自己思考。
如果真心想学习树状数组的话代码看到一维的已经足够了，只是想抄代码的话二维的题肯定没法做出来，毕竟没有裸题对吧，所以这题及后面的题没有贴出代码。
【区间修改，区间查询】
思路：不难证明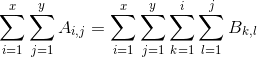
，将以上式子变形成类似一维情形下最终得到的式子即可。
【区间最值】
我去，毒瘤松松松都不会出这种题目吧，因为我不会太毒瘤就不写了吧。。。