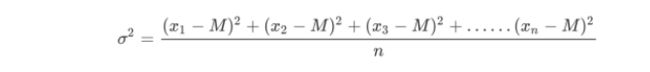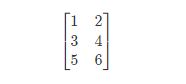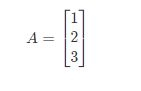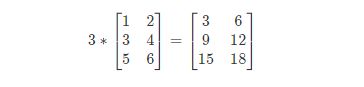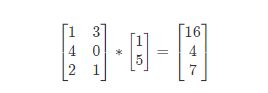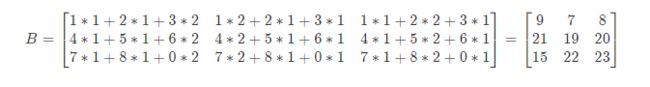Python_机器学习_Numpy（4）

Numpy

学习目标

• 了解Numpy运算速度上的优势
• 知道数组的属性，形状、类型
• 应用Numpy实现数组的基本操作
• 应用随机数组的创建实现正态分布应用
• 应用Numpy实现数组的逻辑运算
• 应用Numpy实现数组的统计运算
• 应用Numpy实现数组之间的运算

4.1 Numpy优势

学习目标

• 目标
  • 了解Numpy运算速度上的优势
  • 知道Numpy的数组内存块风格
  • 知道Numpy的并行化运算

---

1 Numpy介绍

Numpy（Numerical Python）是一个开源的Python科学计算库，用于快速处理任意维度的数组。

Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。

Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

2 ndarray介绍

NumPy provides an N-dimensional array type, the ndarray, 
which describes a collection of “items” of the same type.

NumPy提供了一个N维数组类型ndarray，它描述了相同类型的“items”的集合。

用ndarray进行存储：

import numpy as np

# 创建ndarray
score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])

score

返回结果：

array([[80, 89, 86, 67, 79],
       [78, 97, 89, 67, 81],
       [90, 94, 78, 67, 74],
       [91, 91, 90, 67, 69],
       [76, 87, 75, 67, 86],
       [70, 79, 84, 67, 84],
       [94, 92, 93, 67, 64],
       [86, 85, 83, 67, 80]])

提问:

使用Python列表可以存储一维数组，通过列表的嵌套可以实现多维数组，那么为什么还需要使用Numpy的ndarray呢？

3 ndarray与Python原生list运算效率对比

在这里我们通过一段代码运行来体会到ndarray的好处

import random
import time
import numpy as np
a = []
for i in range(100000000):
    a.append(random.random())

# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间
%time sum1=sum(a)

b=np.array(a)

%time sum2=np.sum(b)

其中第一个时间显示的是使用原生Python计算时间,第二个内容是使用numpy计算时间:

CPU times: user 852 ms, sys: 262 ms, total: 1.11 s
Wall time: 1.13 s
CPU times: user 133 ms, sys: 653 µs, total: 133 ms
Wall time: 134 ms

从中我们看到ndarray的计算速度要快很多，节约了时间。

机器学习的最大特点就是大量的数据运算，那么如果没有一个快速的解决方案，那可能现在python也在机器学习领域达不到好的效果。

Numpy专门针对ndarray的操作和运算进行了设计，所以数组的存储效率和输入输出性能远优于Python中的嵌套列表，数组越大，Numpy的优势就越明显。

思考：

ndarray为什么可以这么快？

4 ndarray的优势

4.1 内存块风格

ndarray到底跟原生python列表有什么不同呢，请看一张图：

从图中我们可以看出ndarray在存储数据的时候，数据与数据的地址都是连续的，这样就给使得批量操作数组元素时速度更快。

这是因为ndarray中的所有元素的类型都是相同的，而Python列表中的元素类型是任意的，所以ndarray在存储元素时内存可以连续，而python原生list就只能通过寻址方式找到下一个元素，这虽然也导致了在通用性能方面Numpy的ndarray不及Python原生list，但在科学计算中，Numpy的ndarray就可以省掉很多循环语句，代码使用方面比Python原生list简单的多。

4.2 ndarray支持并行化运算（向量化运算）

numpy内置了并行运算功能，当系统有多个核心时，做某种计算时，numpy会自动做并行计算

4.3 效率远高于纯Python代码

Numpy底层使用C语言编写，内部解除了GIL（全局解释器锁），其对数组的操作速度不受Python解释器的限制，所以，其效率远高于纯Python代码。

5 小结

• numpy介绍【了解】
  • 一个开源的Python科学计算库
  • 计算起来要比python简洁高效
  • Numpy使用ndarray对象来处理多维数组
• ndarray介绍【了解】
  • NumPy提供了一个N维数组类型ndarray，它描述了相同类型的“items”的集合。
  • 生成numpy对象:np.array()
• ndarray的优势【掌握】
  • 内存块风格
    • list -- 分离式存储,存储内容多样化
    • ndarray -- 一体式存储,存储类型必须一样
  • ndarray支持并行化运算（向量化运算）
  • ndarray底层是用C语言写的,效率更高,释放了GIL

===============================================

4.2 N维数组-ndarray

学习目标

• 目标
  • 说明数组的属性，形状、类型

---

1 ndarray的属性

数组属性反映了数组本身固有的信息。

属性名字	属性解释
ndarray.shape	数组维度的元组
ndarray.ndim	数组维数
ndarray.size	数组中的元素数量
ndarray.itemsize	一个数组元素的长度（字节）
ndarray.dtype	数组元素的类型

2 ndarray的形状

首先创建一些数组。

# 创建不同形状的数组
>>> a = np.array([[1,2,3],[4,5,6]])
>>> b = np.array([1,2,3,4])
>>> c = np.array([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]])

分别打印出形状

>>> a.shape
>>> b.shape
>>> c.shape

(2, 3)  # 二维数组
(4,)    # 一维数组
(2, 2, 3) # 三维数组

如何理解数组的形状？

二维数组：

三维数组：

3 ndarray的类型

>>> type(score.dtype)

dtype是numpy.dtype类型，先看看对于数组来说都有哪些类型

名称	描述	简写
np.bool	用一个字节存储的布尔类型（True或False）	'b'
np.int8	一个字节大小，-128 至 127	'i'
np.int16	整数，-32768 至 32767	'i2'
np.int32	整数，-2^31​ 至 2^32 -1	'i4'
np.int64	整数，-2^63 至 2^63 - 1	'i8'
np.uint8	无符号整数，0 至 255	'u'
np.uint16	无符号整数，0 至 65535	'u2'
np.uint32	无符号整数，0 至 2^32 - 1	'u4'
np.uint64	无符号整数，0 至 2^64 - 1	'u8'
np.float16	半精度浮点数：16位，正负号1位，指数5位，精度10位	'f2'
np.float32	单精度浮点数：32位，正负号1位，指数8位，精度23位	'f4'
np.float64	双精度浮点数：64位，正负号1位，指数11位，精度52位	'f8'
np.complex64	复数，分别用两个32位浮点数表示实部和虚部	'c8'
np.complex128	复数，分别用两个64位浮点数表示实部和虚部	'c16'
np.object_	python对象	'O'
np.string_	字符串	'S'
np.unicode_	unicode类型	'U'

创建数组的时候指定类型

>>> a = np.array([[1, 2, 3],[4, 5, 6]], dtype=np.float32)
>>> a.dtype
dtype('float32')

>>> arr = np.array(['python', 'tensorflow', 'scikit-learn', 'numpy'], dtype = np.string_)
>>> arr
array([b'python', b'tensorflow', b'scikit-learn', b'numpy'], dtype='|S12')

• 注意：若不指定，整数默认int64，小数默认float64

4 总结

数组的基本属性【知道】

属性名字	属性解释
ndarray.shape	数组维度的元组
ndarray.ndim	数组维数
ndarray.size	数组中的元素数量
ndarray.itemsize	一个数组元素的长度（字节）
ndarray.dtype	数组元素的类型

=============================================

4.3 基本操作

学习目标

• 目标
  • 理解数组的各种生成方法
  • 应用数组的索引机制实现数组的切片获取
  • 应用维度变换实现数组的形状改变
  • 应用类型变换实现数组类型改变
  • 应用数组的转换

---

1 生成数组的方法

1.1 生成0和1的数组

• np.ones(shape, dtype)
• np.ones_like(a, dtype)
• np.zeros(shape, dtype)
• np.zeros_like(a, dtype)

ones = np.ones([4,8])
ones

返回结果:

array([[1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1.]])

np.zeros_like(ones)

返回结果:

array([[0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.]])

1.2 从现有数组生成

1.2.1 生成方式

• np.array(object, dtype)

• np.asarray(a, dtype)

a = np.array([[1,2,3],[4,5,6]])
# 从现有的数组当中创建
a1 = np.array(a)
# 相当于索引的形式，并没有真正的创建一个新的
a2 = np.asarray(a)

1.2.2 关于array和asarray的不同

1.3 生成固定范围的数组

1.3.1 np.linspace (start, stop, num, endpoint)

• 创建等差数组 — 指定数量
• 参数:
  • start:序列的起始值
  • stop:序列的终止值
  • num:要生成的等间隔样例数量，默认为50
  • endpoint:序列中是否包含stop值，默认为ture

# 生成等间隔的数组
np.linspace(0, 100, 11)

返回结果：

array([  0.,  10.,  20.,  30.,  40.,  50.,  60.,  70.,  80.,  90., 100.])

1.3.2 np.arange(start,stop, step, dtype)

• 创建等差数组 — 指定步长
• 参数
  • step:步长,默认值为1

np.arange(10, 50, 2)

返回结果：

array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42,
       44, 46, 48])

1.3.3 np.logspace(start,stop, num)

• 创建等比数列

• 参数:

  • num:要生成的等比数列数量，默认为50

# 生成10^x
np.logspace(0, 2, 3)

返回结果:

array([  1.,  10., 100.])

1.4 生成随机数组

1.4.1 使用模块介绍

• np.random模块

1.4.2 正态分布

一、基础概念复习：正态分布（理解）

a. 什么是正态分布

正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ是此随机变量的方差，所以正态分布记作N(μ，σ )。

b. 正态分布的应用

生活、生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。

c. 正态分布特点

μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

标准差如何来？

• 方差

是在概率论和统计方差衡量一组数据时离散程度的度量

其中M为平均值，n为数据总个数，σ 为标准差，σ ^2​可以理解一个整体为方差

• 标准差与方差的意义

可以理解成数据的一个离散程度的衡量

二、正态分布创建方式

• np.random.randn(d0, d1, …, dn)

  功能：从标准正态分布中返回一个或多个样本值

• np.random.normal(loc=0.0, scale=1.0, size=None)

  loc：float

  ​ 此概率分布的均值（对应着整个分布的中心centre）

  scale：float

  ​ 此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）

  size：int or tuple of ints

  ​ 输出的shape，默认为None，只输出一个值

• np.random.standard_normal(size=None)

  返回指定形状的标准正态分布的数组。

举例1：生成均值为1.75，标准差为1的正态分布数据，100000000个

x1 = np.random.normal(1.75, 1, 100000000)

返回结果：

array([2.90646763, 1.46737886, 2.21799024, ..., 1.56047411, 1.87969135,
       0.9028096 ])

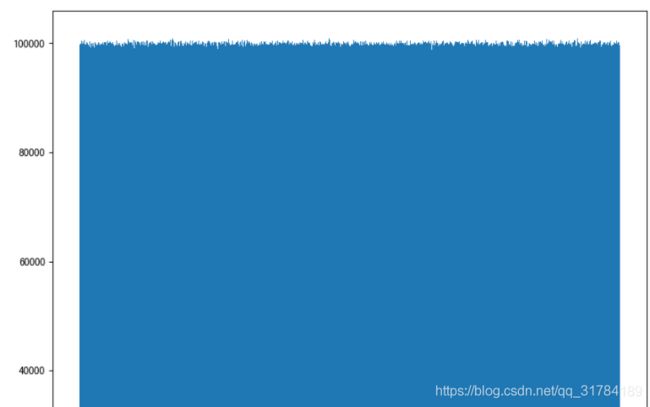
# 生成均匀分布的随机数
x1 = np.random.normal(1.75, 1, 100000000)

# 画图看分布状况
# 1）创建画布
plt.figure(figsize=(20, 10), dpi=100)

# 2）绘制直方图
plt.hist(x1, 1000)

# 3）显示图像
plt.show()

例如：我们可以模拟生成一组股票的涨跌幅的数据

举例2：随机生成4支股票1周的交易日涨幅数据

4支股票，一周(5天)的涨跌幅数据，如何获取？

• 随机生成涨跌幅在某个正态分布内，比如均值0，方差1

股票涨跌幅数据的创建

# 创建符合正态分布的4只股票5天的涨跌幅数据
stock_change = np.random.normal(0, 1, (4, 5))
stock_change

返回结果：

array([[ 0.0476585 ,  0.32421568,  1.50062162,  0.48230497, -0.59998822],
       [-1.92160851,  2.20430374, -0.56996263, -1.44236548,  0.0165062 ],
       [-0.55710486, -0.18726488, -0.39972172,  0.08580347, -1.82842225],
       [-1.22384505, -0.33199305,  0.23308845, -1.20473702, -0.31753223]])

1.4.2 均匀分布

• np.random.rand(d0, d1, ..., dn)
  • 返回[0.0，1.0)内的一组均匀分布的数。
• np.random.uniform(low=0.0, high=1.0, size=None)
  • 功能：从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high.
  • 参数介绍:
    • low: 采样下界，float类型，默认值为0；
    • high: 采样上界，float类型，默认值为1；
    • size: 输出样本数目，为int或元组(tuple)类型，例如，size=(m,n,k), 则输出mnk个样本，缺省时输出1个值。
  • 返回值：ndarray类型，其形状和参数size中描述一致。
• np.random.randint(low, high=None, size=None, dtype='l')
  • 从一个均匀分布中随机采样，生成一个整数或N维整数数组，
  • 取数范围：若high不为None时，取[low,high)之间随机整数，否则取值[0,low)之间随机整数。

# 生成均匀分布的随机数
x2 = np.random.uniform(-1, 1, 100000000)

返回结果：

array([ 0.22411206,  0.31414671,  0.85655613, ..., -0.92972446,
0.95985223,  0.23197723])

画图看分布状况：

import matplotlib.pyplot as plt

# 生成均匀分布的随机数
x2 = np.random.uniform(-1, 1, 100000000)

# 画图看分布状况
# 1）创建画布
plt.figure(figsize=(10, 10), dpi=100)

# 2）绘制直方图
plt.hist(x=x2, bins=1000)  # x代表要使用的数据，bins表示要划分区间数

# 3）显示图像
plt.show()

2 数组的索引、切片

一维、二维、三维的数组如何索引？

• 直接进行索引,切片
• 对象[:, :] -- 先行后列

二维数组索引方式：

• 举例：获取第一个股票的前3个交易日的涨跌幅数据

# 二维的数组，两个维度 
stock_change[0, 0:3]

返回结果：

array([-0.03862668, -1.46128096, -0.75596237])

• 三维数组索引方式：

# 三维
a1 = np.array([ [[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])
# 返回结果
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[12,  3, 34],
        [ 5,  6,  7]]])
# 索引、切片
>>> a1[0, 0, 1]   # 输出: 2

3 形状修改

3.1 ndarray.reshape(shape, order)

• 返回一个具有相同数据域，但shape不一样的视图
• 行、列不进行互换

# 在转换形状的时候，一定要注意数组的元素匹配
stock_change.reshape([5, 4])
stock_change.reshape([-1,10])  # 数组的形状被修改为: (2, 10), -1: 表示通过待计算

3.2 ndarray.resize(new_shape)

• 修改数组本身的形状（需要保持元素个数前后相同）
• 行、列不进行互换

stock_change.resize([5, 4])

# 查看修改后结果
stock_change.shape
(5, 4)

3.3 ndarray.T

• 数组的转置
• 将数组的行、列进行互换

stock_change.T.shape
(4, 5)

4 类型修改

4.1 ndarray.astype(type)

• 返回修改了类型之后的数组

stock_change.astype(np.int32)

4.2 ndarray.tostring([order])或者ndarray.tobytes([order])

• 构造包含数组中原始数据字节的Python字节

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
arr.tostring()

4.3 jupyter输出太大可能导致崩溃问题【了解】

如果遇到

IOPub data rate exceeded.
    The notebook server will temporarily stop sending output
    to the client in order to avoid crashing it.
    To change this limit, set the config variable
    `--NotebookApp.iopub_data_rate_limit`.

这个问题是在jupyer当中对输出的字节数有限制，需要去修改配置文件

创建配置文件

jupyter notebook --generate-config
vi ~/.jupyter/jupyter_notebook_config.py

取消注释,多增加

## (bytes/sec) Maximum rate at which messages can be sent on iopub before they
#  are limited.
c.NotebookApp.iopub_data_rate_limit = 10000000

但是不建议这样去修改，jupyter输出太大会崩溃

5 数组的去重

5.1 np.unique()

temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
>>> np.unique(temp)
array([1, 2, 3, 4, 5, 6])

6 小结

• 创建数组【掌握】

  • 生成0和1的数组
    • np.ones()
    • np.ones_like()
  • 从现有数组中生成
    • np.array -- 深拷贝
    • np.asarray -- 浅拷贝

  • 生成固定范围数组

    • np.linspace()
      • nun -- 生成等间隔的多少个
    • np.arange()
      • step -- 每间隔多少生成数据
    • np.logspace()
      • 生成以10的N次幂的数据

  • 生层随机数组

    • 正态分布
      • 里面需要关注的参数:均值:u, 标准差:σ
        • u -- 决定了这个图形的左右位置
        • σ -- 决定了这个图形是瘦高还是矮胖
      • np.random.randn()
      • np.random.normal(0, 1, 100)
    • 均匀
      • np.random.rand()
      • np.random.uniform(0, 1, 100)
      • np.random.randint(0, 10, 10)

• 数组索引【知道】

  • 直接进行索引,切片
  • 对象[:, :] -- 先行后列

• 数组形状改变【掌握】

  • 对象.reshape()
    • 没有进行行列互换,新产生一个ndarray
  • 对象.resize()
    • 没有进行行列互换,修改原来的ndarray
  • 对象.T
    • 进行了行列互换

• 数组去重【知道】

  • np.unique(对象)

============================================

4.4 ndarray运算

学习目标

• 目标
  • 应用数组的通用判断函数
  • 应用np.where实现数组的三元运算

---

问题

如果想要操作符合某一条件的数据，应该怎么做？

1 逻辑运算

# 生成10名同学，5门功课的数据
>>> score = np.random.randint(40, 100, (10, 5))

# 取出最后4名同学的成绩，用于逻辑判断
>>> test_score = score[6:, 0:5]

# 逻辑判断, 如果成绩大于60就标记为True 否则为False
>>> test_score > 60
array([[ True,  True,  True, False,  True],
       [ True,  True,  True, False,  True],
       [ True,  True, False, False,  True],
       [False,  True,  True,  True,  True]])

# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[ 1,  1,  1, 52,  1],
       [ 1,  1,  1, 59,  1],
       [ 1,  1, 44, 44,  1],
       [59,  1,  1,  1,  1]])

2 通用判断函数

• np.all()

# 判断前两名同学的成绩[0:2, :]是否全及格
>>> np.all(score[0:2, :] > 60)
False

• np.any()

# 判断前两名同学的成绩[0:2, :]是否有大于90分的
>>> np.any(score[0:2, :] > 80)
True

3 np.where（三元运算符）

通过使用np.where能够进行更加复杂的运算

• np.where()

# 判断前四名学生,前四门课程中，成绩中大于60的置为1，否则为0
temp = score[:4, :4]
np.where(temp > 60, 1, 0)

• 复合逻辑需要结合np.logical_and和np.logical_or使用

# 判断前四名学生,前四门课程中，成绩中大于60且小于90的换为1，否则为0
np.where(np.logical_and(temp > 60, temp < 90), 1, 0)

# 判断前四名学生,前四门课程中，成绩中大于90或小于60的换为1，否则为0
np.where(np.logical_or(temp > 90, temp < 60), 1, 0)

4 统计运算

如果想要知道学生成绩最大的分数，或者做小分数应该怎么做？

4.1 统计指标

在数据挖掘/机器学习领域，统计指标的值也是我们分析问题的一种方式。常用的指标如下：

• min(a, axis)
  • Return the minimum of an array or minimum along an axis.
• max(a, axis])
  • Return the maximum of an array or maximum along an axis.
• median(a, axis)
  • Compute the median along the specified axis.
• mean(a, axis, dtype)
  • Compute the arithmetic mean along the specified axis.
• std(a, axis, dtype)
  • Compute the standard deviation along the specified axis.
• var(a, axis, dtype)
  • Compute the variance along the specified axis.

4.2 案例：学生成绩统计运算

进行统计的时候，axis 轴的取值并不一定，Numpy中不同的API轴的值都不一样，在这里，axis 0代表列, axis 1代表行去进行统计

# 接下来对于前四名学生,进行一些统计运算
# 指定列 去统计
temp = score[:4, 0:5]
print("前四名学生,各科成绩的最大分：{}".format(np.max(temp, axis=0)))
print("前四名学生,各科成绩的最小分：{}".format(np.min(temp, axis=0)))
print("前四名学生,各科成绩波动情况：{}".format(np.std(temp, axis=0)))
print("前四名学生,各科成绩的平均分：{}".format(np.mean(temp, axis=0)))

结果：

前四名学生,各科成绩的最大分：[96 97 72 98 89]
前四名学生,各科成绩的最小分：[55 57 45 76 77]
前四名学生,各科成绩波动情况：[16.25576821 14.92271758 10.40432602  8.0311892   4.32290412]
前四名学生,各科成绩的平均分：[78.5  75.75 62.5  85.   82.25]

如果需要统计出某科最高分对应的是哪个同学？

• np.argmax(temp, axis=)
• np.argmin(temp, axis=)

print("前四名学生，各科成绩最高分对应的学生下标：{}".format(np.argmax(temp, axis=0)))

结果：

前四名学生，各科成绩最高分对应的学生下标：[0 2 0 0 1]

5 小结

• 逻辑运算【知道】
  • 直接进行大于,小于的判断
  • 合适之后,可以直接进行赋值
• 通用判断函数【知道】
  • np.all()
  • np.any()
• 统计运算【掌握】
  • np.max()
  • np.min()
  • np.median()
  • np.mean()
  • np.std()
  • np.var()
  • np.argmax(axis=) — 最大元素对应的下标
  • np.argmin(axis=) — 最小元素对应的下标

==========================================

4.5 数组间运算

学习目标

• 目标
  • 知道数组与数之间的运算
  • 知道数组与数组之间的运算
  • 说明数组间运算的广播机制

---

1 数组与数的运算

arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr + 1
arr / 2

# 可以对比python列表的运算，看出区别
a = [1, 2, 3, 4, 5]
a * 3

2 数组与数组的运算

arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])

上面这个能进行运算吗，结果是不行的！

2.1 广播机制

数组在进行矢量化运算时，要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候，就会出现广播机制，该机制会对数组进行扩展，使数组的shape属性值一样，这样，就可以进行矢量化运算了。下面通过一个例子进行说明：

arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)

arr2 = np.array([1,2,3])
arr2.shape
# (3,)

arr1+arr2
# 结果是：
array([[1, 2, 3],
       [2, 3, 4],
       [3, 4, 5],
       [4, 5, 6]])

上述代码中，数组arr1是4行1列，arr2是1行3列。这两个数组要进行相加，按照广播机制会对数组arr1和arr2都进行扩展，使得数组arr1和arr2都变成4行3列。

下面通过一张图来描述广播机制扩展数组的过程：

广播机制实现了时两个或两个以上数组的运算，即使这些数组的shape不是完全相同的，只需要满足如下任意一个条件即可。

• 1.数组的某一维度等长。
• 2.其中一个数组的某一维度为1 。

广播机制需要扩展维度小的数组，使得它与维度最大的数组的shape值相同，以便使用元素级函数或者运算符进行运算。

如果是下面这样，则不匹配：

A  (1d array): 10
B  (1d array): 12
A  (2d array):      2 x 1
B  (3d array):  8 x 4 x 3

思考：下面两个ndarray是否能够进行运算？

arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1], [3]])

3 小结

• 数组运算,满足广播机制,就OK【知道】
  • 1.维度相等
  • 2.shape(其中对应的地方为1,也是可以的)

================================================

4.6 数学：矩阵

学习目标

• 目标
  • 知道什么是矩阵和向量
  • 知道矩阵的加法,乘法
  • 知道矩阵的逆和转置
  • 应用np.matmul、np.dot实现矩阵运算

---

1 矩阵和向量

1.1 矩阵

矩阵，英文matrix，和array的区别矩阵必须是2维的，但是array可以是多维的。

如图:这个是 3×2 矩阵，即 3 行 2 列，如 m 为行，n 为列，那么 m×n 即 3×2

矩阵的维数即行数×列数

矩阵元素(矩阵项):

Aij 指第 i 行，第 j 列的元素。

1.2 向量

向量是一种特殊的矩阵，讲义中的向量一般都是列向量，下面展示的就是三维列 向量(3×1)。)

2 加法和标量乘法

矩阵的加法:行列数相等的可以加。

例:

矩阵的乘法:每个元素都要乘。

例:

组合算法也类似。

3 矩阵向量乘法

矩阵和向量的乘法如图：m×n 的矩阵乘以 n×1 的向量，得到的是 m×1 的向量

例:

1*1+3*5 = 16
4*1+0*5 = 4
2*1+1*5 = 7

矩阵乘法遵循准则：

(M行, N列)*(N行, L列) = (M行, L列)

4 矩阵乘法

矩阵乘法：

m×n 矩阵乘以 n×o 矩阵，变成 m×o 矩阵。

举例：比如说现在有两个矩阵 A 和 B，那 么它们的乘积就可以表示为图中所示的形式。

练一练

• 求矩阵AB的结果

答案：

5 矩阵乘法的性质

矩阵的乘法不满足交换律：A×B≠B×A

矩阵的乘法满足结合律。即：A×（B×C）=（A×B）×C

单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1,我们称 这种矩阵为单位矩阵．它是个方阵，一般用 I 或者 E 表示，从 左上角到右下角的对角线（称为主对角线）上的元素均为 1 以外全都为 0。如：

6 逆、转置

矩阵的逆：如矩阵 A 是一个 m×m 矩阵（方阵），如果有逆矩阵，则：

低阶矩阵求逆的方法:

​ 1.待定系数法

​ 2.初等变换

矩阵的转置：设 A 为 m×n 阶矩阵（即 m 行 n 列），第 i 行 j 列的元素是 a(i,j)，即：

A=a(i,j)

定义 A 的转置为这样一个 n×m 阶矩阵 B，满足 B=a(j,i)，即 b (i,j)=a (j,i)（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），记 AT =B。

直观来看，将 A 的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作 镜面反转，即得到 A 的转置。

例：

7 矩阵运算

7.1 矩阵乘法api：

• np.matmul
• np.dot

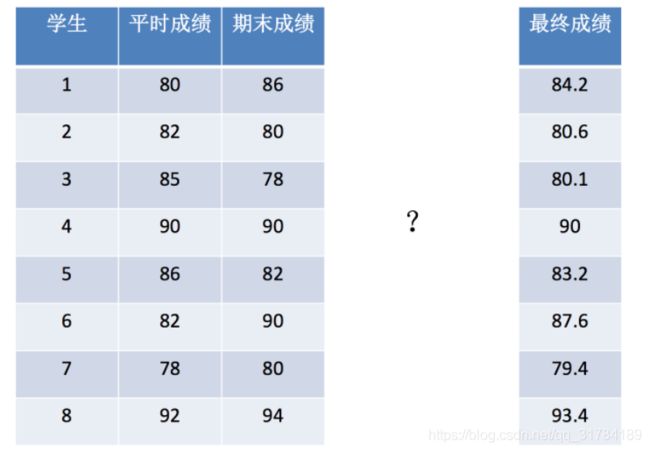
>>> a = np.array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
>>> b = np.array([[0.7], [0.3]])

>>> np.matmul(a, b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

>>> np.dot(a,b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

np.matmul和np.dot的区别:

二者都是矩阵乘法。 np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中，np.matmul与np.dot没有区别。

7 小结

• 1.矩阵和向量【知道】
  • 矩阵就是特殊的二维数组
  • 向量就是一行或者一列的数据
• 2.矩阵加法和标量乘法【知道】
  • 矩阵的加法:行列数相等的可以加。
  • 矩阵的乘法:每个元素都要乘。
• 3.矩阵和矩阵(向量)相乘 【知道】
  • (M行, N列)*(N行, L列) = (M行, L列)
• 4.矩阵性质【知道】
  • 矩阵不满足交换率,满足结合律
• 5.单位矩阵【知道】
  • 对角线都是1的矩阵,其他位置都为0
• 6.矩阵运算【掌握】
  • np.matmul
  • np.dot
  • 注意：二者都是矩阵乘法。 np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中，np.matmul与np.dot没有区别。