Kaggle笔记：Porto Seguro’s Safe Driver Prediction（2）

Porto Seguro’s Safe Driver Prediction

4.特征工程

上一部分完成了对数据的清洗与分析工作，完成这些准备工作之后，接下来准备进行特征工程。特征工程包括对原始数据特征进行检测、变形、筛选，以及构筑新的可能对建立模型有帮助的特征，是机器学习的重要步骤。

首先，读入必要的数据与模块：

import pandas as pd
import numpy as np

test = pd.read_csv('D:\\CZM\\Kaggle\\FinalWork\\train_after_EDA.csv')
train = pd.read_csv('D:\\CZM\\Kaggle\\FinalWork\\test_after_EDA.csv')
len_train = len(train)
len_test = len(test)

4.1 基于缺失值的特征工程

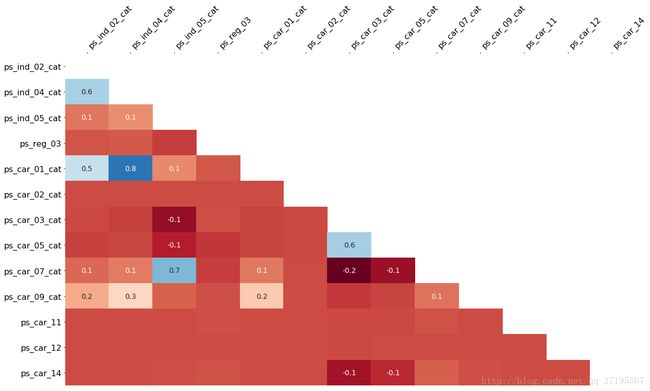
在对缺失值进行分析时，我们发现一部分特征的缺失情况之间存在关联，如下图所示：

2.2已经分析过，ps_ind_02_cat与ps_ind_04_cat、ps_car_01_cat；ps_car_07_cat和ps_ind_05_cat；ps_03_cat和ps_05_cat，这三组特征每组内的特征缺失情况彼此之间存在关联。基于此，尝试构筑以下三个特征：

MissingTotal_1：样本在ps_ind_02_cat、ps_ind_04_cat、ps_car_01_cat这三个特征出现缺失值的个数之和。
MissingTotal_2：样本在ps_car_07_cat和ps_ind_05_cat这两个特征中出现缺失值的个数之和。
MissingTotal_3：样本在ps_car_03_cat和ps_car_05_cat这两个特征中出现缺失值的个数之和。

代码如下：

#基于缺失值构筑特征：
train['MissingTotal_1'] = np.zeros(len_train)
train['MissingTotal_2'] = np.zeros(len_train)
train['MissingTotal_3'] = np.zeros(len_train)
##MissingTotal_1：ps_ind_02_cat、ps_ind_04_cat、ps_ind_04_cat
train['MissingTotal_1'][train.ps_ind_02_cat==-1] += 1
train['MissingTotal_1'][train.ps_ind_04_cat==-1] += 1
train['MissingTotal_1'][train.ps_car_01_cat==-1] += 1
##MissingTotal_2：ps_car_07_cat和ps_ind_05_cat
train['MissingTotal_2'][train.ps_car_07_cat==-1] += 1
train['MissingTotal_2'][train.ps_ind_05_cat==-1] += 1
##MissingTotal_3：ps_car_03_cat和ps_car_05_cat
train['MissingTotal_3'][train.ps_car_03_cat==-1] += 1
train['MissingTotal_3'][train.ps_car_05_cat==-1] += 1

##对测试集进行相同的处理：
test['MissingTotal_1'] = np.zeros(len_test)
test['MissingTotal_2'] = np.zeros(len_test)
test['MissingTotal_3'] = np.zeros(len_test)
##MissingTotal_1：ps_ind_02_cat、ps_ind_04_cat、ps_ind_04_cat
test['MissingTotal_1'][test.ps_ind_02_cat==-1] += 1
test['MissingTotal_1'][test.ps_ind_04_cat==-1] += 1
test['MissingTotal_1'][test.ps_car_01_cat==-1] += 1
##MissingTotal_2：ps_car_07_cat和ps_ind_05_cat
test['MissingTotal_2'][test.ps_car_07_cat==-1] += 1
test['MissingTotal_2'][test.ps_ind_05_cat==-1] += 1
##MissingTotal_3：ps_car_03_cat和ps_car_05_cat
test['MissingTotal_3'][test.ps_car_03_cat==-1] += 1
test['MissingTotal_3'][test.ps_car_05_cat==-1] += 1

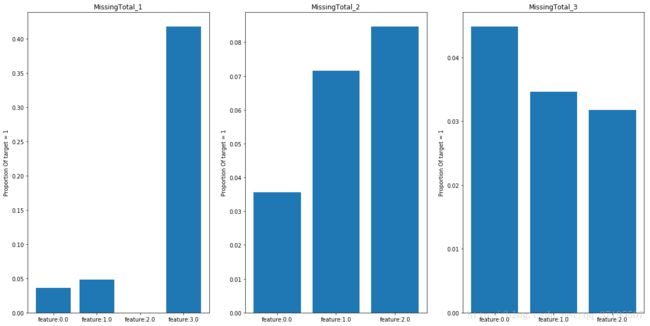
接下来，我们要分析新增的变量与Target变量的关系：

##作图观察三个特征与Target变量的关系：
k = 0
plt.figure(figsize=(20,10))
for x in Missing_Total:
    k = k+1
    plt.subplot(1,3,k)
    names = [];prop = []
    va = train[x].value_counts().index
    for name in va:
        names.append('feature:'+str(name))
        props = train[train[x]==name].target.value_counts()
        prop_1 = 0;prop_0 = 0
        if 1 in props.index:prop_1 = props[1]
        if 0 in props.index:prop_0 = props[0]
        prop.append(prop_1/(prop_1+prop_0))
    plt.ylabel('Proportion Of target = 1')
    plt.bar(names,prop)

计算target=1关于这三个新特征的条件概率，可以看到根据这些新特征的不同取值，target=1的样本所占的比例是有显著不同的，说明这些特征可能对target的预测能起到作用。

4.2 基于二分类变量的特征工程

在2.4分析相关系数矩阵时，我们发现了以下的二分类特征之间具有相关性：

• ps_ind_06_bin、ps_ind_07_ bin、ps_ind_08_bin、ps_ind_09_ bin这四列，相互之间均具有较强的负相关。
• ps_ind_16_bin、ps_ind_17_bin、ps_ind_18_bin这三列，相互之间均具有较强的负相关。
• 此外，ps_ind_15和ps_ind_16_bin之间存在较强的负相关；ps_ind_15与ps_ind_16_bin之间也存在一定的正相关。

由于二分类变量的取值是0-1的，所以，这里可以尝试对彼此之间相关的二分类特征求和建立新特征：

bin_plus_1：ps_ind_06_bin、ps_ind_07_bin、ps_ind_08_bin、ps_ind_09_ bin这四列相加。
bin_plus_2：ps_ind_16_bin、ps_ind_17_bin、ps_ind_18_bin这三列相加。

##基于bin特征构造特征：
train['bin_plus_1'] = train['ps_ind_06_bin']+train['ps_ind_07_bin']+train['ps_ind_08_bin']+train['ps_ind_09_bin']
train['bin_plus_2'] = train['ps_ind_16_bin']+train['ps_ind_17_bin']+train['ps_ind_18_bin']

但是，查看第一个新特征bin_plus_1的分布，会发现：

In [145]: train.bin_plus_1.value_counts()
Out[145]: 
1    595212
Name: bin_plus_1, dtype: int64

所有的样本这一特征的值都是相同的，这一特征虽然因此不能够使用了，但是我们提取出了新的信息：对于每个样本，这四个特征之和都必定为1，换言之，其中至少有一个特征是没有必要的。

剔除刚刚新增的bin_plus_1，除此之外，还将ps_ind_09_ bin这一特征列从数据集中删除：

##发现bin_plus_1的值为1，说明这四个特征之和必定为1。
##剔除bin_plus_1和ps_ind_09_bin
train = train.drop('bin_plus_1',axis = 1)
train = train.drop('ps_ind_09_bin',axis = 1)
test = test.drop('ps_ind_09_bin',axis = 1)

接下来，因为二分类特征发生了变化，因此，需要重新绘制相关系数矩阵图：

能够看到ps_ind_06、ps_ind_07、ps_ind_08彼此之间仍存在一定负相关，但是幅度已经降低不少。那么，重新用这三个特征的和构筑bin_plus_1，另外，也在测试集中构筑bin_plus_1与bin_plus_2：

##重新构筑：
train['bin_plus_1'] = train['ps_ind_06_bin']+train['ps_ind_07_bin']+train['ps_ind_08_bin']
test['bin_plus_1'] = test['ps_ind_06_bin']+test['ps_ind_07_bin']+test['ps_ind_08_bin']
test['bin_plus_2'] = test['ps_ind_16_bin']+test['ps_ind_17_bin']+test['ps_ind_18_bin']

此外，实际上通过相关系数矩阵图，也可以发现之前新增的一些特征与其他特征之间存在相关性，不过这里暂时不考虑这些。

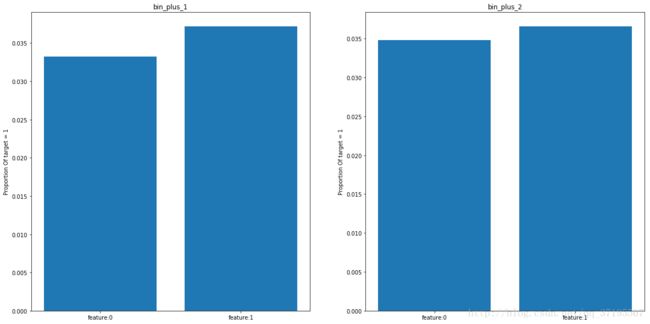
接下来，我们要分析新增的变量与Target变量的关系：

可以看到新增的特征取值对Target的影响不大，可能不是很好的特征，不过，总之也可以先留着，之后再进行筛选。

另外，可以发现这两个新增的特征都属于二维变量：

bincol.append('bin_plus_1')
bincol.append('bin_plus_2')

4.3 对多分类特征的处理

数据集中存在14个标记为_cat的多分类特征，不过，根据先前的分析我们已经得知，这14个多分类特征中，实际上存在两个特征：ps_car_08_cat以及ps_ind_04_cat，它们属于二分类特征，其中ps_ind_04_cat是存在缺失值的，因此也可以视为多分类特征，但是ps_car_08_cat就必须被剔除出多分类变量：

#把ps_car_08_cat剔除出多分类：
catcol.remove('ps_car_08_cat')
bincol.append('ps_car_08_cat')

接下来，待分析的多分类变量特征还剩13个。常用的对多分类变量进行的建模方法是根据多分类特征的取值，将其转化为多个二维的哑变量，然后再进行建模。然而这样做有两个缺点：第一，这会导致数据维数迅速上升，对本地计算机来说运算压力过大；第二，可能会导致本应反映各个取值之间的关系的一定信息流失。

这篇论文详细介绍了一种根据变量的各个取值下目标变量的似然概率，将分类变量转化为连续变量的方法：https://kaggle2.blob.core.windows.net/forum-message-attachments/225952/7441/high%20cardinality%20categoricals.pdf

这里本项目也将采用这种方法。

但是在执行以前，必须考虑到另一个事实：从先前的分析结果来看，数据集中很可能存在特征被错误归类的情况，有二维特征被归入了多分类的特征，而且，ps_car_11_cat特征可取的值实在是太多了，有100多个，比起多分类变量，它更像是一个顺序或定距变量特征。

在这种情况下，认为现有的分类特征很可能会存在由顺序或定距变量误分过来的特征，是一个合理的推断。因此，对于多分类特征，本项目作出的处理如下：

• 为所有多分类特征留存一份副本，将这些变量类型视为连续或顺序变量，缺失值也重新插补为中位数。

• 然后将原本的多分类特征，按照前述方法根据Target似然概率转化为连续变量特征。

  ##为所有多分类特征留存一份副本，重新插补缺失值，视为顺序变量特征：
  cat_to_rank_col = []
  for x in catcol:
      name = x+'_rank'
      co = train[x]
      co = co.replace(-1,np.nan)
      co = co.replace(np.nan,co.median())
      cat_to_rank_col.append(name)
      train[name] = co
  
  for x in catcol:
      name = x+'_rank'
      co = test[x]
      co = co.replace(-1,np.nan)
      co = co.replace(np.nan,co.median())
      test[name] = co
  
  ##接下来，把所有原本的多分类特征，根据贝叶斯概率转化为连续型特征：
  y = train.target
  nTR = len(y)
  nY = len(y[y==1])
  nYTR = nY/nTR
  for coll in catcol:
      cat1 = train[coll]
      cat2 = train[coll][y==1]
      cat3 = test[coll]
      valuec1 = cat1.value_counts()
      valuec2 = cat2.value_counts()
      catdict = {}
      for i in valuec1.index: 
          ind = i
          ni = valuec1[ind]
          if ind in valuec2.index:
              niY = valuec2[ind] 
          else:
              niY = 0
          lamda = 1/(1+np.exp(20-0.1*ni))
          smoothing = lamda*niY/ni+(1-lamda)*nYTR
          catdict[ind] = smoothing
      #print (catdict)
      for i in valuec1.index: 
          cat1[cat1==i] = catdict[i]
          cat3[cat3==i] = catdict[i]
      train[coll] = cat1
      test[coll] = cat3
  

到此，多分类特征处理完成了，数据集中已经只剩下二维变量与连续、顺序变量。
接下来会对所有的连续或顺序变量进行分析。

4.4 剔除训练集与测试集分布不同的特征

也许是数据提供方刻意为之，也可能纯粹是因为数据集足够大，总之，根据第2、3节的内容，在大多数的特征上，训练集与测试集的分布十分接近。不过，仍然存在几个在训练集和测试集中取值的分布不同的特征，那就是ps_calc_06，ps_calc_12，ps_calc_13，ps_calc_14这四个特征。

但是，直接剔除可能会损失信息，根据3.3节，ps_calc_06的取值小于2、ps_calc_12的取值大于6、ps_calc_13的取值等于13、ps_calc_14的取值等于19，都可能会对Target=1的条件概率造成比较明显的影响。

为了保留这些信息，设定4个新的二维变量特征：

ps_calc_06_bin：ps_calc_06的取值小于2时记为1，否则为0。
ps_calc_12_bin：ps_calc_12的取值大于6时记为1，否则为0。
ps_calc_13_bin：ps_calc_13的取值等于13时记为1，否则为0。
ps_calc_14_bin：ps_calc_14的取值等于19时记为1，否则为0。

然后，剔除原始特征。

##calc_bin：
train['ps_calc_06_bin'] = np.zeros(len_train)
train['ps_calc_12_bin'] = np.zeros(len_train)
train['ps_calc_13_bin'] = np.zeros(len_train)
train['ps_calc_14_bin'] = np.zeros(len_train)
train['ps_calc_06_bin'][train.ps_calc_06<2] += 1
train['ps_calc_12_bin'][train.ps_calc_12>6] += 1
train['ps_calc_13_bin'][train.ps_calc_13==13] += 1
train['ps_calc_14_bin'][train.ps_calc_14==19] += 1
test['ps_calc_06_bin'] = np.zeros(len_test)
test['ps_calc_12_bin'] = np.zeros(len_test)
test['ps_calc_13_bin'] = np.zeros(len_test)
test['ps_calc_14_bin'] = np.zeros(len_test)
test['ps_calc_06_bin'][test.ps_calc_06<2] += 1
test['ps_calc_12_bin'][test.ps_calc_12>6] += 1
test['ps_calc_13_bin'][test.ps_calc_13==13] += 1
test['ps_calc_14_bin'][test.ps_calc_14==19] += 1
train=train.drop('ps_calc_06',axis = 1)
train=train.drop('ps_calc_12',axis = 1)
train=train.drop('ps_calc_13',axis = 1)
train=train.drop('ps_calc_14',axis = 1)
test=test.drop('ps_calc_06',axis = 1)
test=test.drop('ps_calc_12',axis = 1)
test=test.drop('ps_calc_13',axis = 1)
test=test.drop('ps_calc_14',axis = 1)

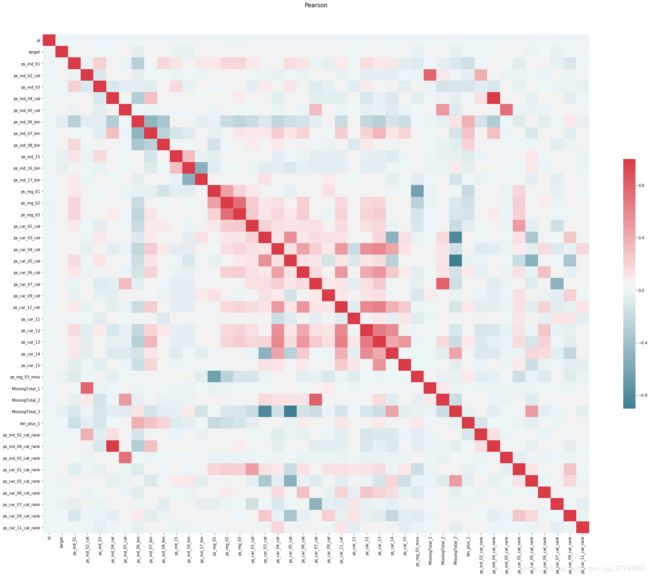
4.5 基于连续或顺序特征以及相关系数矩阵的分析

原始数据集中不存在_bin或_cat后缀的特征属于连续或顺序变量，但是，本段所讨论的连续或顺序特征不仅是这些，也包括了已经根据贝叶斯概率转化为连续变量的原本的多分类特征。

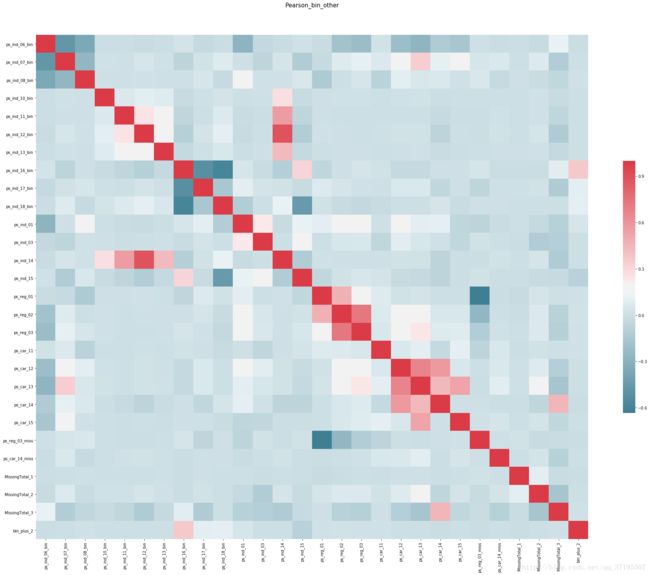
由于此时数据中已经不存在多分类特征，因此，重新对整个训练集的所有特征画相关系数矩阵图：

从图中能够取得的信息如下：

• 即使经过了多次特征工程，我们可以看到calc类的特征依然如先前看到的一样，不与任何其他特征存在相关关系。
• 经过连续化处理后的多分类变量整体之间存在一定的正相关关系，且与reg类特征之间也存在一定的正相关关系。
• ps_ind_04_cat与ps_car_10_cat、ps_car_02_cat，与经过顺序化后的它们自己，也就是ps_ind_04_cat_rank和ps_car_10_cat_rank，ps_car_02_cat_rank之间存在较强的相关性，实际上，可以说整个cat特征区域，都与cat_rank区域之间有一定的相关性，这意味着这些多分类特征的特征取值大小顺序可能是有意义的。
• MissingTotal_1与ps_ind_02_cat之间存在较强的正相关，MissingTotal_2与ps_car_07_cat之间正相关，由于MissingTotal是多个特征（包括这里出现的与之相关的特征）的缺失值数目之和，这可能说明了ps_ind_02_cat的缺失值在构成MissingTotal_1的三个特征中起主要作用，MissingTotal_2与ps_car_07_cat同理。而MissingTotal_3与构成它的两个特征ps_car_03_cat和ps_car_05_cat均呈现较强的负相关就很好理解了，这两个特征的缺失值都较多。

以上信息是与先前对比，新的相关系数矩阵带来的新内容。

4.6，使用随机森林与XGBoost尝试对数据建模

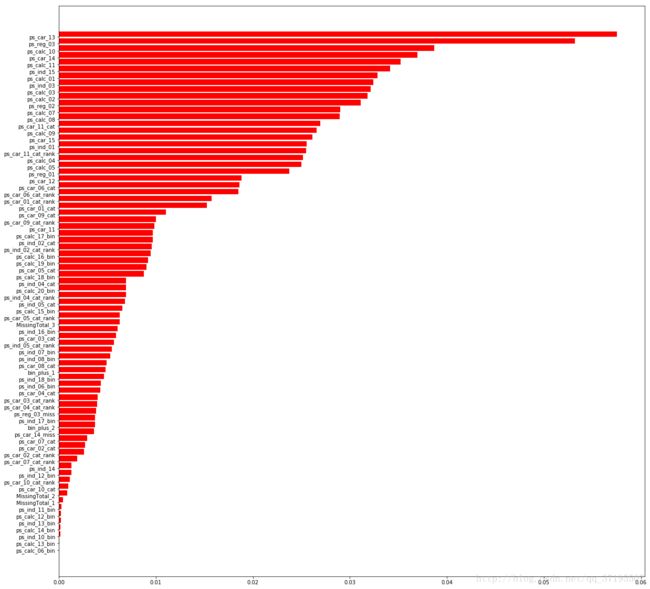
接下来将会对现有的数据集尝试用随机森林模型进行建模，这两种模型作为组合树模型拥有自动选取特征的能力，它们提供的特征重要性排序，会有助于特征的筛选工作。

首先，使用SKlearn包对整个训练集建立随机森林模型：

##尝试建模，目标是输出特征重要性
##1.RandomForest
from sklearn.ensemble import RandomForestClassifier
model_fe = RandomForestClassifier()
features = train.columns[2:]
model_fe.fit(train[features],train.target)
###重要性排序
importance = model_fe.feature_importances_
features_sort = features[np.argsort(importance)[::-1]]
importance_sort = importance[np.argsort(importance)[::-1]]
plt.figure(figsize = (20,20))
sorted_idx = np.argsort(importance)[::-1]
pos = np.arange(sorted_idx.shape[0]) + .5
plt.barh(pos, importance[sorted_idx[::-1]],color='r',align='edge')
plt.yticks(pos, features[sorted_idx[::-1]])

上图是对是随机森林输出的特征重要性进行排序后的示意图，从图中我们可以看到，ps_car_13和ps_reg_03无疑是最为重要的两个特征。先前一直不看好的calc类特征也有很多占据了较高的重要性排序上，而先前字形构造的的ps_calc_06_bin、ps_calc_12_bin、ps_calc_13_bin、ps_calc_14_bin、MissingValue_1、MissingValue_2等几个特征基本没有贡献。

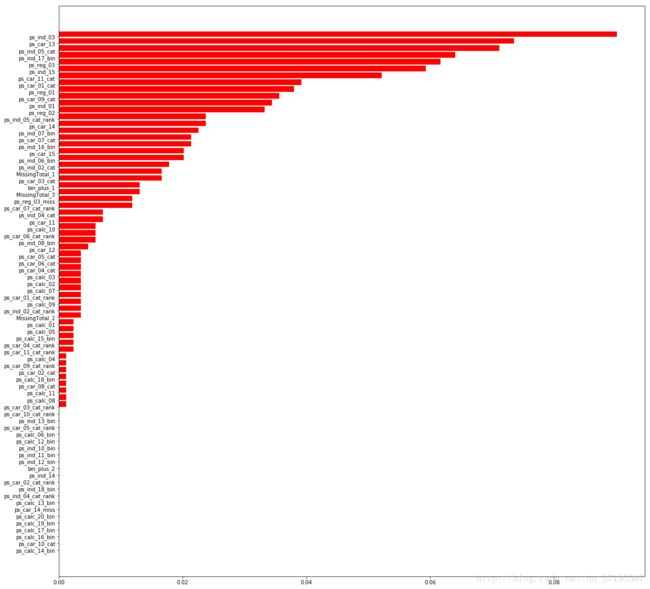
接下来，尝试使用XGBoost进行建模：

##2.XGBoost
import xgboost as xgb
from xgboost import XGBClassifier
model_fe = XGBClassifier(    
                        n_estimators=70,
                        max_depth=6,
                        objective="binary:logistic",
                        subsample=.8,
                        min_child_weight=6,
                        colsample_bytree=.8,
                        scale_pos_weight=1.6,
                        gamma=10,
                        reg_alpha=8,
                        reg_lambda=1.3,
                     )
model_fe.fit(train[features],train.target)
###重要性排序
importance = model_fe.feature_importances_
features_sort = features[np.argsort(importance)[::-1]]
importance_sort = importance[np.argsort(importance)[::-1]]
plt.figure(figsize = (20,20))
sorted_idx = np.argsort(importance)[::-1]
pos = np.arange(sorted_idx.shape[0]) + .5
plt.barh(pos, importance[sorted_idx[::-1]],color='r',align='edge')
plt.yticks(pos, features[sorted_idx[::-1]])

可以看到，XGBOOST模型的重要性排序认为ps_ind_03才是最重要的特征，ps_car_13和ps_ind_05_cat次之，而和随机森林相比，XGBoost输出的特征重要性有更多贡献极低的特征，和随机森林输出的重要性特征排序不同，XGBoost认为几乎所有的calc类特征都不会给出什么贡献，而先前我们自己构筑的MissingTotal_1和MissingTotal_3以及bin_plus_1都拥有不错的特征重要性。

这里，把在两个模型中特征重要性的排序都很低的特征剔除，它们是：

##因重要性过低，将会被剔除的特征：

useless_features = [
 'ps_car_04_cat_rank',
 'ps_car_02_cat',
 'ps_car_08_cat',
 'ps_car_03_cat_rank',
 'ps_car_10_cat_rank',
 'ps_ind_13_bin',
 'ps_calc_06_bin',
 'ps_calc_12_bin',
 'ps_ind_10_bin',
 'ps_ind_11_bin',
 'ps_ind_12_bin',
 'bin_plus_2',
 'ps_ind_14',
 'ps_car_02_cat_rank',
 'ps_ind_18_bin',
 'ps_calc_13_bin',
 'ps_car_14_miss',
 'ps_car_10_cat',
 'ps_calc_14_bin']

train = train.drop(useless_features,axis = 1)
test = test.drop(useless_features,axis = 1)

共计19个特征被剔除，剩余的特征有56个。

4.7 剔除强相关特征

在完成绝大多数的特征工程后，再一次画出相关系数矩阵：

可以看到，经过几番特征处理过后，较为严重的特征之间的相关性已经很少见了。reg与car类特征之间虽然存在一定的线性相关区域，但是程度也是可以接受的。

接下来，我们要处理掉剩余存在强线性相关情况的几个点：MissingTotal_3与ps_car_03_cat和ps_car_05_cat都具有较强的负相关，而MissingTotal_2也与ps_car_07有较强的正相关，此外，ps_ind_04_cat与ps_ind_04_cat_rank之间也存在很强的正相关。

为此，可以选择删除出现了强线性相关，在模型特征评分中表现也不好的ind_04_cat_rank，MissingTotal_3，MissingTotal_2：

#删除强相关特征：
cor_features = ['ps_ind_04_cat_rank','ps_car_03_cat','MissingTotal_2']
train = train.drop(cor_features,axis = 1)
test = test.drop(cor_features,axis = 1)

此外，还能够发现，target目标变量几乎不和其他特征存在明显的线性相关性，因此，应该意识到线性模型在这样的数据集上，很难有良好的表现。

4.8 总结

至此特征工程告一段落，原始数据被添加和删除了大量特征后，剩余特征的总数为53，如无意外，这就将会是用于建模的最终数据。

那么，把完成了特征工程的数据集保存好：

##保存数据

train.to_csv('D:\\CZM\\Kaggle\\FinalWork\\train_after_FeatureEngineer.csv', index=False)
test.to_csv('D:\\CZM\\Kaggle\\FinalWork\\test_after_FeatureEngineer.csv', index=False)