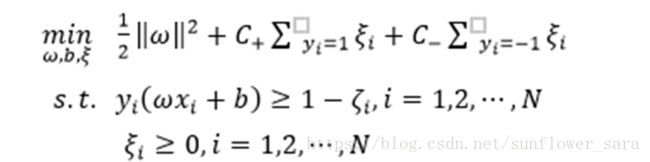数据不均衡问题的解决
目录
数据不均衡问题可以使用的方法:
1. 使用正确指标评估权值
2. 采样
3.数据合成
4.算法层面
分类器算法上的改进
代价敏感学习算法(Cost-Sensitive Learning)
例子:改进分类器的代价函数:C-SVC算法的SVM
数据不均衡问题可以使用的方法:
一、使用正确指标评估权值
AUC_ROC ACC SPEC SENS PPV NPV MCC F1score AUC_PRC
二、数据层面
1. 数据重采样
1).欠抽样
删减大比例类的样本量
2).过抽样
增加小比例类的样本量
| 上采样 | 下采样 | |
|---|---|---|
| 使用情况 | 数据不足时 | 数据充足 (支撑得起你的浪费) |
| 数据集变化 | 增加 | 间接减少(量大类被截流了) |
| 具体手段 | 大量复制量少类样本;数据扩充 | 批处理训练时,控制从量大类取的图像数量 |
| 风险 | 过拟合 |
2. 类别平衡采样
通过设计 样本列表 来实现平衡采样。
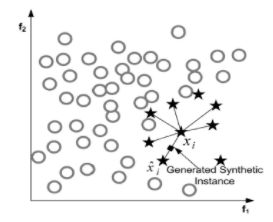
3.数据合成
eg:SMOTE算法
概念:
合成少数类过采样技术,利用小众样本在特征空间的相似性来生成新样本
算法流程:
(1)对于少数类中每一个样本x,欧氏距离为标准计算它到少数类样本集中所有样本的距离,得到其k近邻。
(2)根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择若干个样本,假设选择的近邻为Xn。
(3)对于每一个随机选出的近邻Xn,分别与原样本按照如下的公式构建新的样本。
算法的缺陷:
该算法主要存在两方面的问题:
1)在近邻选择时,存在一定的盲目性
需要根据实验结果调整临近点数
2)容易产生分布边缘化问题
可能将边缘复制,产生模糊的边界
3)人造数据不靠谱
三、算法层面
在目标函数中,增加 量少类 样本 被错分 的 损失值 。
1. 基于代价敏感矩阵的代价敏感
利用 K×KK×K 的 矩阵CC 对不同样本类别施加错分惩罚。
在目标函数中,增加量少类样本被错分的损失值 。
准确度这个评价指标在类别不均衡的分类任务中并不能work.
代价敏感学习算法(Cost-Sensitive Learning)
不同类型的五分类情况导致的代价是不一样的。因此定义代价矩阵,Cij表示将类别j误分类为i的代价,显然C00=C11=0.C01和C10为两种不同的误分类代价,当两者相等时为代价不敏感的学习问题。
![]()
代价敏感学习方法主要有以下的实现方式:
(1)从学习模型出发,着眼于对某一具体学习方法的改造,使之能适应不平衡数据下的学习,研究者们针对不同的学习模型如感知机,支持向量机,决策树,神经网络等分别提出了其代价敏感的版本。以代价敏感的决策树为例,可从三个方面对其进行改进以适应不平衡数据的学习,这三个方面分别是决策阈值的选择方面、分裂标准的选择方面、剪枝方面,这三个方面中都可以将代价矩阵引入。
(2)从贝叶斯风险理论出发,把代价敏感学习看成是分类结果的一种后处理,按照传统方法学习到一个模型,以实现损失最小为目标对结果进行调整,优化公式如下所示。此方法的优点在于它可以不依赖所用具体的分类器,但是缺点也很明显它要求分类器输出值为概率。
![]()
(3)从预处理的角度出发,将代价用于权重的调整,使得分类器满足代价敏感的特性。
例子:改进分类器的代价函数:C-SVC算法的SVM
对于少类和多类,分别采用不同的惩罚系数c,使得超平面向一类方向偏移
2. 基于代价敏感向量的代价敏感
每个样本 都具有自己的 代价敏感矩阵。一旦这样些代价敏感矩阵相同,则该方法 退化 为“基于代价敏感矩阵的代价敏感向量”。
Example:
- Focal Loss
focal loss 的出现,是一个伟大的里程碑。它的出现,直接将类别不平衡处理从原来繁杂的人工时代进化到了 纯计算时代 。管你类别再不平衡,只需一个简单的公式,统统搞定:
其中pt为:
展开来看,Kaiming 大神的 Focal Loss 形式是:
![]()
如果落实到 ŷ =σ(x) 这个预测,那么就有:
![]()
特别地,如果 K 和 γ 都取 1,那么 L∗∗=Lfl。
事实上 K 和 γ 的作用都是一样的,都是调节权重曲线的陡度,只是调节的方式不一样。注意 L∗∗ 或 Lfl 实际上都已经包含了对不均衡样本的解决方法,或者说,类别不均衡本质上就是分类难度差异的体现。
比如负样本远比正样本多的话,模型肯定会倾向于数目多的负类(可以想象全部样本都判为负类),这时候,负类的 ŷ γ 或 σ(Kx) 都很小,而正类的 (1−ŷ )γ 或 σ(−Kx) 就很大,这时候模型就会开始集中精力关注正样本。
当然,Kaiming 大神还发现对 Lfl 做个权重调整,结果会有微小提升。
![]()
通过一系列调参,得到 α=0.25, γ=2(在他的模型上)的效果最好。注意在他的任务中,正样本是属于少数样本,也就是说,本来正样本难以“匹敌”负样本,但经过 (1−ŷ )γ 和 ŷγ 的“操控”后,也许形势还逆转了,还要对正样本降权。
参考资料:
https://blog.csdn.net/u013102349/article/details/79309198
https://blog.csdn.net/jningwei/article/details/79249195
https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/78920998