问题的提法是:给定一个没有负权值的有向图和其中一个点src作为源点(source),求从点src到其余个点的最短路径及路径长度。求解该问题的算法一般为Dijkstra算法。
假设图顶点个数为n,则针对其余n-1个点需要分别找出点src到这n-1个点的最短路径。Dijkstra算法的思想是贪心法,先找出最短的那条路径,其次找到次短的,再找到第三短的,依次类推,直到找完点src到达其余所有点的最短路径。下面举例说明算法和贪心过程。
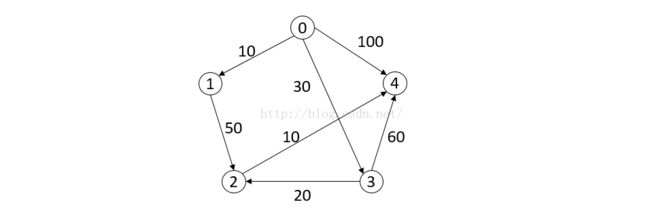
如下图所示(该图源自《数据结构预(用面向对象方法与C++语言描述)(第2版)》殷人昆 主编清华大学出版社),求顶点0到其余个点的最短路径其路径长度。
说明一下,下面表述过程中有一个【直接到达】,例如 从点0直接到达点K意思是有一条边从0指向K。
从定点0出发能直接达到点1、3、4,不能直接到达的点,认为点0直接到达这些点的距离为无穷大,所以这些直接路径中,最短的路径为0到1,长度为10。可以认定,从0到点1的最短路径就是0→1,否则,假设存在另外一条从0到1的路径,经过其他点,例如点k,使得该路径0→k+k→3的路径长度<10,然而已知,从0直接到达除1之外的其他点k的距离 > 从0直接到达点1的距离,所以这条路径不可能是最短路径。这样,就找出了从0到1的最短路径。
然后,找出从0直接到达其他的点最短路径,最短为0→3,路径长度为30,那么能否像确定0→1一样确定0→3为从0到达3的最短路径呢?不能,因为有可能存在另外一条从0到3的路径,经过其他点,例如k,使得该路径0→k+k→3的路径长度<30,因为存在0→k的长度<30,所以有可能 路径(0→k)+(k→3)的路径长度<30,所以需要验证一下这种可能是否存在。
上面通过实例对Dijkstra算法的贪心过程进行了简单说明,下面给出算法过程。
Dijkstra算法过程:设图的邻接矩阵为G[n][n],顶点集合为V,G[i][j]表示从i到j的直线距离,求定点v到达其他定点的最短路径及路径长度。
Step1:令集合S={v},集合S用于存储已经找到从v到达该点的最短路径的顶点,dist[i]用于存储v到i的最短路径长度,初始化的时候令dist[i] = G[v][i](i取遍V-S中所有的点)。
Step2:寻找k使得dist[k]= min{dist[i]},令S=S+{k}(注意这里+表示取两个集合的并集)。
Step3:更新dist[i] = min { dist[i],dist[k]+G[k][i] } (i取遍V-S中所有的点)。
Step4:判断,若S==V,则停止算法,dist[i]即为v到i的最短路径长度;否则,转到Step2。
下面给出不严密证明:
v作为源点,算法开始的时候,没有找到任何点的最短路径,所以Step2寻找k使得dist[k]= min{dist[i]},此时k的最短路径已经找到,长度即为dist[k],因为从v直接到达到k的路径最短,若让v经过其他点再到达k,必然使得路径增长(这也是为什么要求图上的权值非负)。所以v到k路径找到,将k加入到集合S中。
进而Step3,看能否让从v到其他点i的路径经过k再到i,使得路径变短,若能则更改路径长度,否则不改变。这样到Step2继续找最短路径,寻找k使得dist[k]= min{dist[i]},对于找到的顶点k,最短路径也找到了的。如此循环下去,直到找到从v到所有点的最短路径。
Step4判断,是否从v到达所有点的最短路径都已经找到,即S==V。
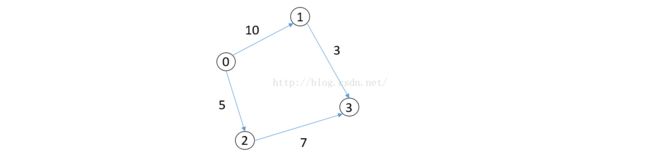
问题1:在Step2和Step3中可能出现这样如图的问题,0为源点,首先选出最短路径的点一次为2和1,那么在仅剩下3,在运行Step2的时候,就需要考虑 dist[3] = min{dist[3],dist[1]+G[1][3]},dist[3]=无穷,达到3的最短路径必须通过1,这样最短路径为0->1->3,长度为13,比0->2->3的路径长度12要长,出现错误!错误在于,在这里进行Step2之前,在上一次循环中Step3的时候,已经对dist[3]进行更新,更新为dist[3] = min{dist[3],dist[2]+G[2][3]},dist[3]=无穷大,dist[2]+G[2][3]=5+7=12,所以下一次循环的时候,dist[3]=12而非无穷,dist[3]=min{dist[3],dist[1]+G[1][3]}=12,
这样就不会出错了。关键是每一步都对没有找到的最短路径的点的路径长度进行了更新。
问题2:dist[i]记录了从v到达i的最短路径长度,如何记录从v到达每个点的具体的最短路径呢?
利用Dijkstra算法求出来的最短路径的特点:任取从v到达k的最短路径上的一个点i(非v非k),那么这条路径上从v到i的那部分路径就是从v到i的最短路径,因为Dijkstra是按照路径长度递增的顺序求最短路径的。这样,就可以在每次求出v到达一个点k的最短路径的时候,记录k之前的那个点,最后逆向即可找到具体路径。
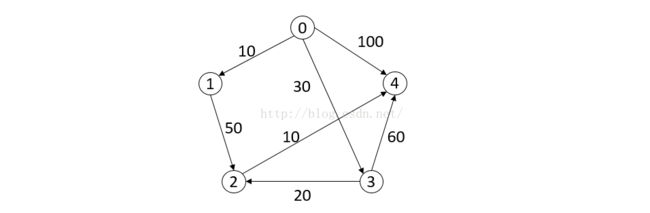
下面通过Dijkstra算法求解前面的例子。
如图,求顶点0到其余个点的最短路径其路径长度。
初始化:S={0},dist[1]=10,dist[2]=INF,dist[3]=30,dist[4]=100,INF表示无穷大。另外增加一个数组path,记录找到最短路径的点之前的那个点,初始化的时候都初始化为path[i]=0(源点)。
Step2:min{dist[1]=10,dist[2]=INF,dist[3]=30,dist[4]=100}=dist[1],所以S={0,1}。
Step3:更新dist[]数组,dist[2]=min{dist[2],dist[1]+G[1][2]}=min{INF,10+50}=60,path[2]=1;
dist[3]=min{dist[3],dist[1]+G[1][3]}=min{30,10+INF}=30,path[3]不改变;
dist[4]=min{dist[4],dist[1]+G[1][4]}=min{100,10+INF}=100,path[4]不改变;
Step2:min{dist[2]=60,dist[3]=30,dist[4]=100}=dist[3],所以S={0,1,3}。
Step3:更新dist[]数组,dist[2]=min{dist[2],dist[3]+G[3][2]}=min{60,30+20}=50,path[2]=3;
dist[4]=min{dist[4],dist[3]+G[3][4]}=min{100,30+60}=90,path[4]=3;
Step2:min{dist[2]=50,dist[4]=90}=dist[2],所以S={0,1,3,2};
Step3:更新dist[]数组,dist[4]=min{dist[4],dist[2]+G[2][4]}=min{90,50+10}=60,path[4]=2;
Step2:只有dist[4]一个了,min{dist[4]}=dist[4],所以S={0,1,3,2,4}==V,停止算法。
对于1,path[1]=0,找到源点0,所以最短路径为0—>1,路径长度为dist[1]=10。
对于2,path[2]=3,path[3]=0,找到源点0,所以最短路径为0—>3—>2,路径长度为dist[2]=50。
对于3,path[3]=0,找到源点0,所以最短路径为0—>3,路径长度为dist[3]=30。
对于4,path[4]=2,path[2]=3,path[3]=0,所以最短路径为0—>3—>2—>4,路径长度为dist[4]=60。
用Dev-C++编写的C++代码:
#include
using namespace std;
int INF = 9999999;
void Dijkstra(int *d[],int dist[],int path[],int n,int src)
{ //dist[i]记录从源点src到点i的路径长度,path[i]记录最短路径上点i前面的那个点
for(int i=0;i //最短路径的点,后面条件表明路径经过点k则路径变短
{
dist[i] = dist[k] + d[k][i]; //更改路径长度
path[i] = k; //那么点i之前的那个点就是点k
}
}
//下面检验是否退出循环---所有点是否都在S当中
bool ok = true;
for(int i=0;i //并且该数组类型为 int* 类型
for(int i=0;i0;i--)
cout << Road[i] << "->";
cout << Road[0] << endl;
}
}
return 0;
} 如有纰漏,请指正!