推荐系统（九）Factor Machines

背景

有时系统中用户的行为比较稀少，采集到的样本很稀疏，这样直接导致常用的拟合方法学到的模型存在严重的过拟合问题，即特征之间存在严重的依赖和隔离关系，使得模型无法进一步学习到精准的内在规律。为了解决这一问题，FM模型应运而生，其基本原理是学到特征与特征之间的关系，从而达到更加精准的预测的目的。

递进

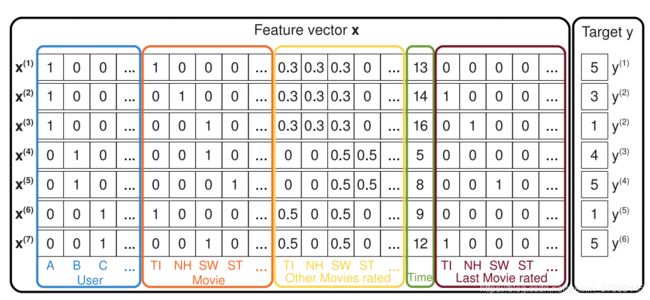
引用论文原文的图示，图中的一条样本描述了当前用户的id特征、当前物品的id特征、当前用户对其他物品的打分、时间、当前用户上次对物品的打分，这条样本的label是当前用户对当前物品的打分。

可以看出，整个矩阵比较稀疏，通常意义下LR模型都会为每一维特征分配一个权重，公式如下所示：
$$\hat{y}(x)=w_0+\sum _{i=1}^n{w}_i{x}_i$$

FM 模型与上述公式不同的地方在于其添加了一个$V(n\times k)$矩阵，$V$的每一行代表的是$x$的某个特征本身的"特征"，具体公式如下所示：
$$\hat{y}(x)=w_0+\sum _{i=1}^n{w}_i{x}_i+\sum _{i=1}^n\sum _{j=i+1}^n⟨v_i,v_j⟩x_i{x}_j$$

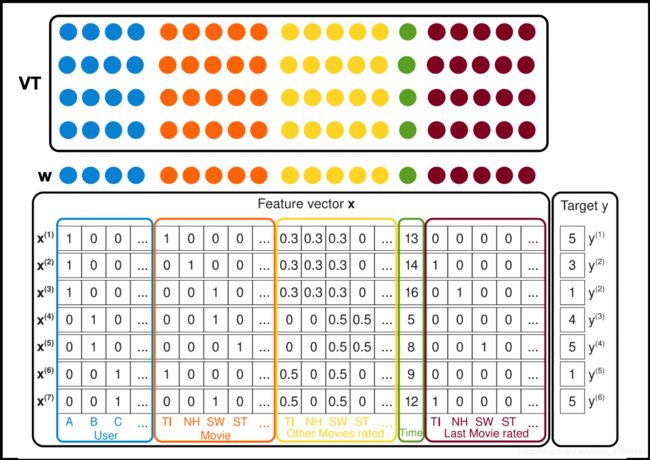
示意图如下所示：

这里$⟨v_i,v_j⟩={\sum }_{f=1}^k{v}_{i,f}{v}_{j,f}$，代表的是$x_i$和$x_j$之间的相互关系。而上述红色公式这样设定的原因我个人理解是因为其描述的是两个不同特征之间的关系，同一个特征之间的关系没有学习的意义，即学习的关系如下所示(蓝色为需要学习的领域，白色为不需要学习的领域)：

可以看出上述公式的时间复杂度为$O(k{n}^2)$，但是这个时间复杂度可以优化到$O(kn)$，公式推导如下所示：

上述公式的梯度下降计算公式如下：
$$\frac{\partial \hat{y}(x)}{\partial \theta }=\{\begin{array}{c}1\theta =w_0\\ x_i\theta =w_i\\ x_i{\sum }_{j=1}^n{v}_{j,f}{x}_j-v_{i,f}{x}_i^2\theta =v_{i,f}\end{array}$$
乍一看模型反向传播的计算时间复杂度为$O(n^2)$，但后来发现针对$v_{i,f}$的梯度计算，${\sum }_{j=1}^n{v}_{j,f}{x}_j$已经在前向传播中计算过一遍，只需要把之前的结果保存下来就行，因而这里只需要计算$v_{i,f}{x}_i^2$，因而$V$的反向传播计算时间复杂度依然是线性的。

代码实现

用最简单的方式来阐述FM前向推导的整体过程：

import tensorflow as tf

X = tf.constant([[1, 2, 3, 4]], dtype=tf.float16)

w_0 = tf.constant([0.5], dtype=tf.float16)
W = tf.constant([[5], [6], [7], [8]], dtype=tf.float16)
V = tf.constant([[1, 2, 3, 4],[1, 2, 3, 4]], dtype=tf.float16)

linear_output = tf.add(w_0, tf.matmul(X, W))

# 公式[1] \sum((X * V^T)^2 - (X^2 * (V^T)^2)) * 0.5
complex_output = tf.multiply(tf.reduce_sum(tf.subtract(tf.pow(tf.matmul(X, tf.transpose(V)), 2), \
                                tf.matmul(tf.pow(X, 2), tf.pow(tf.transpose(V), 2))), \
                                           axis=1, keep_dims=True), 0.5)
final_output= tf.add(linear_output, complex_output)

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    print(complex_output.shape, complex_output.eval())
>>> (1, 1) [[546.]]

在写这段代码之前，确实有些疑惑，代码的实现方式和论文中的公式有所不同，代码中的实现方式有些难以理解，但是当我们仔细展开公式，发现二者确实是一样的，初始化$X$和$V$如下所示：
$$X=[x_1,x_2,x_3,x_4]$$

$$V=\left[\begin{array}{cccc}{v}_{11}& v_{12}& v_{13}& v_{14}\\ v_{21}& v_{22}& v_{23}& v_{24}\end{array}\right]$$

上述FM核心代码的公式[1]的推导如下所示(格式有些乱，但是思路比较清晰)：
$$\begin{array}{r}complex\_out=\frac{1}{2}\sum _{f=1}^2((\sum _{i=1}^4{v}_{i,f}{x}_i{)}^2-\sum _{i=1}^4{v}_{i,f}^2{x}_i^2)\\ =\frac{1}{2}[(v_{11}{x}_1+v_{21}{x}_2+v_{31}{x}_3+v_{41}{x}_4{)}^2\\ -(v_{11}^2{x}_1^2+v_{21}^2{x}_2^2+v_{31}^2{x}_3^2+v_{41}^2{x}_4^2)]\\ +\frac{1}{2}[(v_{12}{x}_1+v_{22}{x}_2+v_{32}{x}_3+v_{42}{x}_4{)}^2-\\ (v_{12}^2{x}_1^2+v_{22}^2{x}_2^2+v_{32}^2{x}_3^2+v_{42}^2{x}_4^2)]\\ =\frac{1}{2}[(v_{11}{x}_1+v_{21}{x}_2+v_{31}{x}_3+v_{41}{x}_4,\\ v_{12}{x}_1+v_{22}{x}_2+v_{32}{x}_3+v_{42}{x}_4{)}^2\\ -(v_{11}^2{x}_1^2+v_{21}^2{x}_2^2+v_{31}^2{x}_3^2+v_{41}^2{x}_4^2,\\ v_{12}^2{x}_1^2+v_{22}^2{x}_2^2+v_{32}^2{x}_3^2+v_{42}^2{x}_4^2)]\\ =reduce\_sum(\frac{1}{2}[(X\ast V^T{)}^2-(X^2\ast (V^T{)}^2)])\end{array}$$

知识分析

这段时间在看张俊林老师的知乎博客，因而在这里总结下我能够理解的知识点。印象较深的有两点：1. FM模型作为召回模型如何在工程中使用，2. 统一召回和多路召回的优缺点，因而我也抄录部分内容作为自己知识点的扩充。

FM召回模型

• 只考虑User和Item各自的特征

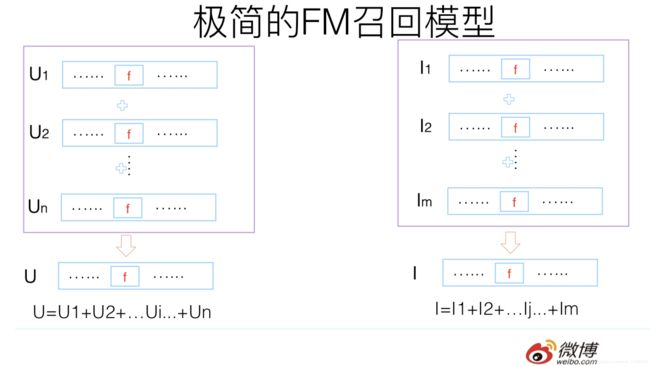
  将单个User每一维User相关特征的embedding叠加起来，作为$U$，并将所有的User的$U$放入redis中，将单个Item每一维Item相关特征的embedding叠加起来，作为$I$，并将所有的Item的$I$放入faiss中，如下图所示：

  

  当一个User请求打过来时，通过这个User对应的$U$去faiss选出与这个$U$ topK相关的$I$，具体计算方式即为$U$和$I$的点积，而能够这样做的原因恰恰是FM的原理，即在只考虑User和Item各自独立特征时，可以看出如下公式的等价关系(借用上面公式)，
  $$\sum _{i=1}^n\sum _{j=i+1}^n⟨v_i,v_j⟩x_i{x}_j=\sum _{i=1}^n\sum _{j=i+1}^n⟨x_i\ast v_i,x_j\ast v_j⟩=⟨\sum _{i=1}^n{x}_i\ast v_i,\sum _{j=1,j\ne i}^n{x}_j\ast v_j⟩$$
  而如果在这里只考虑User和Item各自的特征，则上述公式可以转化为：
  $$⟨\sum _{i=1}^n{x}_i\ast v_i,\sum _{j=1,j\ne i}^n{x}_j\ast v_j⟩=⟨\sum _i{U}_i,\sum _j{I}_j⟩$$

• 添加context信息

  context信息只能够通过线上实时获取，比如用户当时的播放行为等等，这里设context信息为$C$，相应的做法也很简单，就是将User和Context的向量叠加后得到$U+C$，而后去faiss通过内积的方式取出topK相关的$I$，如下图所示：

统一召回 VS 多路召回

• 统一召回的优点

1. 多路召回的召回得分不可比，统一召回的得分是有意义的。但是在实际操作中，其实往往不去看多路召回的得分，只去看特征，比如这个资源是不是音乐，播放时长是多少。
2. 如果采用多路召回，每一路召回多少个Item这个超参确实比较难调(可以从现有的系统中调研下)
3. 多路召回会存在ranking和recall存在割裂感，比如增加了一路召回，但是ranking却没有添加相应的特征在模型中，使得这一路召回的Item没办法排上来

• 多路召回的优点

1. 上线比较灵活，新增一种召回方式对线上整体的召回系统影响较小，系统的稳定性较好

参考文献

1. FM paper
2. FM公式推导
3. 张俊林 推荐系统召回四模型之：全能的FM模型