UKF原理与实现

卡尔曼滤波家族主要有KF、EKF、UKF三兄弟。KF主要应用于系统方程和量测方程为线性的的场景，EKF应用于轻度非线性场景，而UKF则在强非线性情况下有更好的表现。这里只介绍UKF。
在KF中，我们需要求取状态协方差来确定卡尔曼增益，但是由于系统存在非线性，只能得到它的近似值。EKF通过雅可比矩阵对系统进行线性化，而UKF则是利用随机采样的条件均值代替均值，使用被估计量和量测量的再现样本点计算两者的自协方差阵和互协方差阵($UT$变换）。

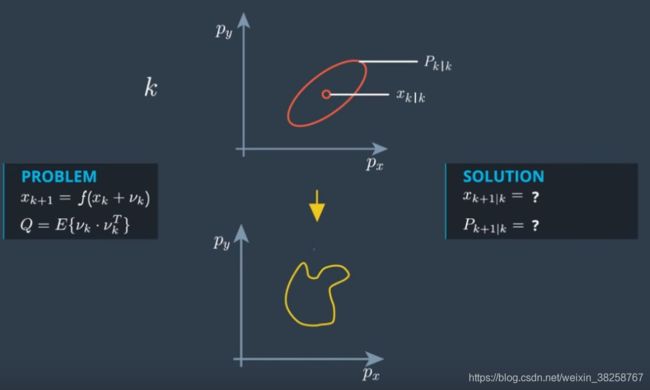
UT变换

对于一维状态变量的情况，可以将这个过程看作是选取${\mu }_x,{\mu }_x+{\sigma }_x,{\mu }_x-{\sigma }_x$三个点，用非线性变换$g$投影过去，再拟合出一个高斯分布。

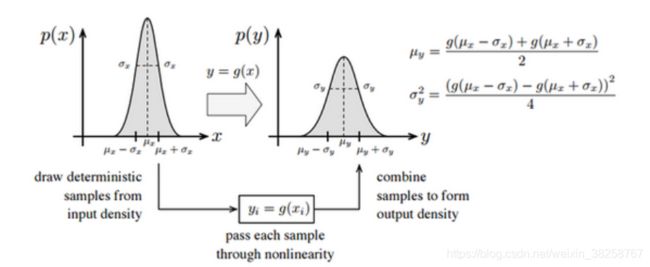
$UT$变换的步骤如下：
假设$n$维随机向量$X$经$f(\cdot )$非线性变换后形成$m$维随机向量$Y$,即
$$Y=f(X)$$,在已知$X$的均值$\bar{X}$和方差阵$P_{XX}$的情况下,求$Y$的均值$\bar{Y}$和$P_{YY}$

步骤1：
根据$\bar{X}$和$P_{XX}$增广出$2n+1$个$X$的1倍$\sigma$样本点。
$${\chi }^{(0)}=\bar{X}$$
$${\chi }^{(i)}=\bar{X}+(\sqrt{(n+\lambda )P_{XX}}{)}_{(i)}i=1,2,...,n$$
$${\chi }^{(i)}=\bar{X}-(\sqrt{(n+\lambda )P_{XX}}{)}_{(i-n)}i=n+1,n+2,...,2n$$
式中，$(\sqrt{(n+\lambda )P_{XX}}{)}_{(i)}$表示矩阵$(n+\lambda )P_{XX}$的下三角分解平方根的第$i$列，为$n$维列向量。
步骤2：
计算非线性变换产生的样本点：
$$Y^{(i)}=f[{\chi }^{(i)}]$$
步骤3：
确定权值
$$W_0^{(m)}=\frac{\lambda }{n+\lambda }$$
$$W_0^{(c)}=\frac{\lambda }{n+\lambda }+1-{\alpha }^2+\beta$$
$$W_i^{(m)}=W_i^{(c)}=\frac{\lambda }{2(n+\lambda )}i=1,2,...,2n$$
上式中，$$\lambda ={\alpha }^2(n+\kappa )-n$$
$\alpha$是很小的正数，可取$10^{-4}\le \alpha \le 1$;$\kappa =3-n$;$\beta$取值与$X$的分布有关，对于正太分布，$\beta =2$为最优值。
步骤4：
确定映射的均值和方差阵
$$\bar{Y}\approx {\Sigma }_{i=0}^{2n}{W}_i^{(m)}{Y}^{(i)}$$
$$P_{YY}\approx {\Sigma }_{i=0}^{2n}{W}_i^{(c)}[Y^{(i)}-\bar{Y}][Y^{(i)}-\bar{Y}{]}^T$$

UKF过程

步骤1，选定滤波初值：
$${\hat{X}}_0=E{X}_0$$
$$P_0=E[(X_0-{\hat{X}}_0)(X_0-{\hat{X}}_0{)}^T]$$
步骤2，计算$k-1$时刻的$2n+1$个$\sigma$样本点
$${\chi }^{(0)}=\bar{X}$$
$${\chi }^{(i)}=\bar{X}+\gamma (\sqrt{P_{k-1}}{)}_{(i)}i=1,2,...,n$$
$${\chi }^{(i)}=\bar{X}-\gamma (\sqrt{P_{k-1}}{)}_{(i-n)}i=n+1,n+2,...,2n$$
上式中，$\gamma =\sqrt{n+\lambda }$


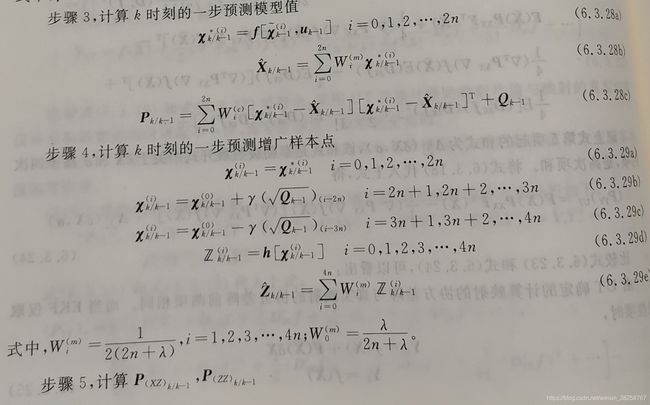
C++实现：
https://github.com/realjc/fusion-ukf

参考链接：
https://zhuanlan.zhihu.com/p/35729804
https://www.cnblogs.com/gaoxiang12/p/5560360.html
https://drivingc.com/p/5b46b7af2392ec1a513a8773
卡尔曼滤波与导航原理P228 秦永元等