聚类算法
聚类算法
- 聚类算法
- K-means聚类
- K-mediods(K中心点)算法
- K-means++聚类
- 二分均值法聚类
- ISODATA
- DBSCAN算法
- OPTICS聚类——DBSCAN改进算法
- Density peak聚类——Clustering by fastsearch and find of density peaks
- 层次聚类方法(AGNES, DIANA)
- AGNES(AGglomerative NESting)算法
- DIANA算法(Divisive ANAlysis)
- 层次聚类方法的改进——BIRCH
- 有序聚类
- 参考
聚类算法
聚类算法的核心——类见距离大,类内距离小
分类是分析已有的数据,寻找其共同的属性,并根据分类模型将这些数据划分成不 同的类别
聚类预先不知道欲划分类的情况下,根 据信息相似度原则进行信息聚类的一种方法

K-means聚类
1、随机的取 k 个点作为 k 个初始质心;
2、计算其他点到这个 k 个质心的距离;
3、如果某个点 p 离第 n 个质心的距离 更近,则该点属于 cluster n;
4、计算同一 cluster 中所有点的平均 值,作为新的质心;
5、重复第2、3步至所有质心不变化为 止,即算法结束。
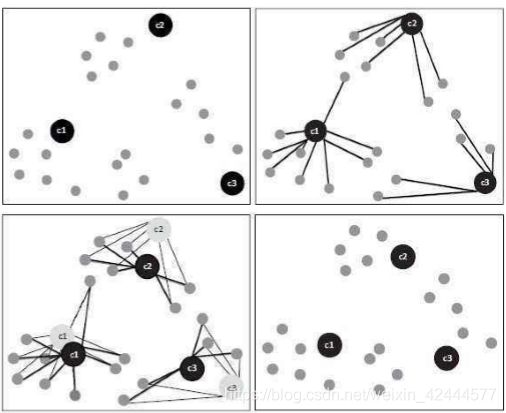
缺点:
(1) 不能拟合最佳聚类数;
(2) 初始聚类中心随机性;
(3) 不断聚类调整,时间开销大;
(4) 受异常点影响极大;
(5) 不适用于非球形分布数据。
K-mediods(K中心点)算法
与K-means相似
步骤1:随机选取一组聚类样本作为中心点集
步骤2: 每个中心点对应一个簇
步骤3:计算各样本点到各个中心点的距离,将样本点放入距离中心点最短的那个簇中
步骤4:计算各簇中,距簇内各样本点距离的绝度误差最小的点,作为新的中心点
绝对误差应该是与k-means唯一的差别了吧
步骤5:如果新的中心点集与原中心点集相同或者算法收敛,算法终止;如果新的中心点集与原中心点集不完全相同或不满足收敛条件,返回步骤2)
K-means++聚类
核心思想:
初始聚类中心相互之间应该分得越开越好
先后选择K个聚类中心,使初始聚类中心的差值最大化


例子

取6作为聚类中心点

P(x)为被选为下一个聚类中心的概率(聚类中心之间距离应该越远越好)
取一个0-1的随机数,比如所得随机数R=0.5,在区间[0.2, 0.525]之间,那么第二个聚类中心为2,理论上距离越近,则被选择为聚类中心的概率越小
二分均值法聚类
基本思路:
首先将所有点作为一个类,然后将该簇一分为二,之后选择其中一个簇继续进行划分,选择哪一个簇进行划取决于对其划分是否可以最大程度降低SSE的值,上述基于SSE的别分过程不断重复,直到得到用户指定的属数目为止。


SSE(和方差、误差平方和):The sum of squares dueto error
ISODATA
- 动态调整聚类中心的数目
- 需要一个预期的聚类中心数目K,最终数目为 [K/2, 2K]
- 如果某个类中样本分散程度较大(通过方差进行衡量)并且样本数量较大,则对其进行分裂操作
- 如果某两个类别靠得比较近(通过聚类中心的距离衡量),则对它们进行合并操作
DBSCAN算法
密度聚类方法思想:只要一个区域中的点的密度大于某个域 值,就把它加到与之相近的聚类中去。这类算法能克服基于 距离的算法只能发现“类圆形”的聚类的缺点,可发现任意 形状的聚类,且对噪声数据不敏感。但计算密度单元的计算 复杂度大,需要建立空间索引来降低计算量,且对数据维数 的伸缩性较差。这类方法需要扫描整个数据库,每个数据对 象都可能引起一次查询,因此当数据量大时会造成频繁的 I / O 操作
DBSCAN:将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在有“噪声”的空间数据库中发现任意形状的聚类
OPTICS聚类——DBSCAN改进算法
OPTICS聚类算法是基于密度的聚类算法,全称是Ordering points to identify the clustering structure,目标是将空间中的数据按照密度分布进行聚类,其思想和DBSCAN非常类似,但是和DBSCAN不同的是,OPTICS算法可以获得不同密度的聚类,直接说就是经过OPTICS算法的处理,理论上可以获得任意密度的聚类。因为OPTICS算法输出的是样本的一个有序队列,从这个队列里面可以获得任意密度的聚类。
参数:半径ε,最少点数MinPts
核心距离:对于核心点,距离其第MinPts近的点与之的距离
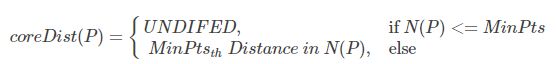
可视距离:对于核心点P,O到P的可达距离定义为O到P的距离或者P的核心距离

算法:
输入:样本集D, 邻域半径E, 给定点在E领域内成为核心对象的最小领域点数MinPts
输出:具有可达距离信息的样本点输出排序
方法:
1、创建两个队列,有序队列和结果队列。
(有序队列用来存储核心对象及其该核心对象的直接可达对象,并按可达距离升序排列;结果队列用来存储样本点的输出次序。你可以把有序队列里面放的理解为待处理的数据,而结果队列里放的是已经处理完的数据)
2、如果所有样本集D中所有点都处理完毕,则算法结束。否则,选择一个未处理(即不在结果队列中)且为核心对象的样本点,找到其所有直接密度可达样本点,如果这些样本点不存在于结果队列中,则将其放入有序队列中,并按可达距离排序;
取一个未处理的核心对象点和他的密度可达样本点放入有序队列
3、如果有序队列为空,则跳至步骤2(处理完毕,重新选取处理数据)。否则,从有序队列中取出第一个样本点(即可达距离最小的样本点)进行拓展,并将取出的样本点保存至结果队列中(如果它不存在结果队列当中的话)。然后进行下面的处理。
从获得的点中取可达距离最小的点放入结果队列
3.1.判断该拓展点是否是核心对象,如果不是,回到步骤3如果该点是核心对象,则找到该拓展点所有的直接密度可达点;
(因为若不是核心对象,就无法进行扩展了。那么就回到步骤3里面,取最小的。这里要注意,第二次取不是取第二小的,因为第一小的已经放到了结果队列中了,所以第二小的就变成第一小的了。)。
3.2.判断该直接密度可达样本点是否已经存在结果队列,是则不处理,否则下一步;
3.3.如果有序队列中已经存在该直接密度可达点,如果此时新的可达距离小于旧的可达距离,则用新可达距离取代旧可达距离,有序队列重新排序(因为一个对象可能直接由多个核心对象可达,因此,可达距离近的肯定是更好的选择);
选出未处理点,更新可达距离
3.4.如果有序队列中不存在该直接密度可达样本点,则插入该点,并对有序队列重新排序;
4、迭代2,3。
5、算法结束,输出结果队列中的有序样本点。

1、X轴代表OPTICS算法处理点的顺序,y轴代表可达距离。
2、簇在坐标轴中表述为凹陷(山谷??Valley),并且凹陷越深,簇越紧密
3、黄色代表的是噪声,它们不形成任何凹陷。
当你需要提取聚集的时候,参考Y轴和图像,自己设定一个阀值就可以提取聚集了。这里将阀值设为0.1就挺合适的。
Density peak聚类——Clustering by fastsearch and find of density peaks
算法核心思想是在聚类中心的选取上,算法认为聚类中心具有以下两个特点:
1、聚类中心局部密度较大
2、聚类中心之间的距离较大
给定数据集S={xi |xi属于Rn ,i=1,… ,N} ,对于每一个样本点xi, xi 计算两个量化值:局部密度值 ρi 和距离密度更高的样本点的聚类 δi
局部密度:

局部密度就是以截断距离dc作为邻域内点的个数
距离计算:

对于密度值为局部或全局最大的样本点而言,它们的δi会比其他样本点的δj值要大很多(如图所示),因为前者代表局部密度最大的样本点之间的距离,而后者代表样本点与其对应的局部密度最大的样本点之间的距离。因此,那些δ值很大的样本点也很有可能就是聚类中心。
步骤:
1、计算每个点的密度值ρi与距离值δi
2、根据两变量画出决策图,确定聚类中心
3、根据聚类中心确定每个类的核心部分与边缘部分(噪声)。

左图是原始点,右图两个变量是密度值和距离值得出的决策图,可以判断10和1是聚类中心
类边缘和核心部分确定:
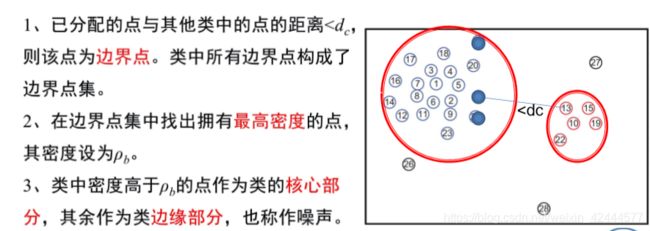
聚类数的确定


一种方法是通过斜率确定,找出斜率改变最大的点

使用Density peak方法,随着样本点数量增多,聚类错误率在逐渐下降。当样本点达到 1000-10000时,聚类错误率大概在 1%以下。
该方法只需要确定一个参数——截断距离dc
如果 dc 太大,那么每个数据点的密度值都近似相等,导致所有数据点 被划分至同一个类簇中;如果 dc太小,每个类簇包含的样本点会很少,很有可能出现同一个类簇被分割成好几部分的情况;合适的dc应该使 数据点的平均近邻数目占整个数据集规模的比例为τ
![]()
dc 的确定缺乏理论依据; 可能会带来不同的聚类结果

优点:
该聚类算法可以得到非球形的聚类结果,可以很好地描述数据 分布,同时在算法复杂度上也比一般的K-means算法的复杂度低。同时此算法的只考虑点与点之间的距离,因此不需要将点映射到一个向量空间中。
缺点:
聚类数量无法直接优化
层次聚类方法(AGNES, DIANA)
层次聚类方法对给定的数据集进行层次的分解,直到某种条件满足为止,可分为:
**凝聚的层次聚类:**一种自底向上的策略,首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到某个终结条件被满足。
**分裂的层次聚类:**采用自顶向下的策略,它首先将所有对象置于一个簇中,然后逐渐细分为越来越小的簇,直到达到了某个终结条件。
层次凝聚的代表是AGNES算法。层次分裂的代表是DIANA算法
AGNES(AGglomerative NESting)算法
算法思想:最初将每个对象作为一个簇,然后这些簇根据某些准则被一步步地合并。两个簇间的相似 度由这两个不同簇中距离最近的数据点对的相似度来确定。聚类的合并过程反复进行直到 所有的对象最终满足簇数目。
AGNES算法(自底向上凝聚算法)
输入:包含n个对象的数据库,终止条件簇的数目k。
输出:k个簇,达到终止条件规定簇数目。
(1) 将每个对象当成一个初始簇;
(2) REPEAT
(3) 根据两个簇中最近的数据点找到最近的两个簇;
(4) 合并两个簇,生成新的簇的集合;
(5) UNTIL 达到定义的簇的数目.

距离测算


AGNES算法例子



假设数据集共有N个样本,第k次合并后的簇数为:N-k
AGNES算法比较简单,但经常会遇到合并点选择的困难。假如一旦一组对象被合并,下一步的处理将在新生成的簇上进行。已做处理不能撤消,聚类之间也不能交换对象。如果在某一步没有很好的选择合并的决定,可能会导致低质量的聚类结果。
• AGNES算法不具有很好的可伸缩性,因为合并的决定需要检查和估算大量的对象或簇。
• 假定在开始的时候有n个簇,在结束的时候有1个簇,因此在主循环中有n次迭代,在第i次迭代中,必须在n-i+1个簇中找到最靠近的两个簇进行合并。另外算法必须计算所有对象两两之间的距离,其复杂度为O(n2)。该算法的时间复杂度为O(n3)。对于n很大的情况是不适用的。
DIANA算法(Divisive ANAlysis)
DIANA(Divisive ANAlysis)算法是典型的分裂聚类方法。
在聚类中,用户能定义希望得到的簇数目作为一个结束条件。同时,它使用下面两种测度方法:


案例:


缺点:
(1)已做的分裂操作不能撤销,类之间不能交换对象。
(2)如果在某一步没有选择好分裂点,可能会导致低质量的聚类结果。
(3)DIANA聚类算法不具有很好的可申缩性,因为分裂的决定需要检查和估算大量的对象或簇。
层次聚类方法的改进——BIRCH
BIRCH(利用层次方法的平衡迭代归约和聚类)(Balanced Iterative Reducing and Clustering Using Hierarchies)
是一个综合的层次聚类方法,它用聚类特征和聚类特征树(CF)来概括聚类描述。该算法通过聚类特征可以方便地进行中心、半径、直径及类内、类间距离的运算。
CF树是一个具有两个参数分支因子B和阈值T的高度平衡树,存储了层次聚类的聚类特征。分支因子定义了每个非叶节点子聚类的最大数目(内部节点最大CF数数),而阈值给出了存储在树的叶子节点中的子聚类的最大直径(叶子节点最大CF数)

定义1:CF是一个三元组,可以用(N,LS,SS)表示。其中N代表了这个CF中拥有的样本点的数量;LS代表了这个CF中拥有的样本点各特征维度的和向量,SS代表了这个CF中拥有的样本点各特征维度的平方和。





聚类特征数:
插入操作:
- 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点
- 如果新样本加入后,这个CF节点对应的超球体半径仍然满足小于阈值T,则更新路径上所有的CF三元组,插入结束。否则转入3
- (超球体半径大于阈值T)如果当前叶子节点的CF节点个数小于阈值L,则创建一个新的CF节点,放入新样本,将新的CF节点放入这个叶子节点,更新路径上所有的CF三元组,插入结束。否则转入4。
- 将当前叶子节点划分为两个新叶子节点,选择旧叶子节点中所有CF元组里超球体距离最 远的两个CF元组,分布作为两个新叶子节点的第一个CF节点。将其他元组和新样本元组按 照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂,如果需要按和 叶子节点分裂方式相同
后续操作:
将所有的样本依次读入,在内存中建立一颗CF Tree。
将第一步建立的CF Tree进行筛选,去除一些异常CF节点,这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并。
利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类,得到一颗比较好的CF Tree。这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构,以及一些由于节点CF个数限制导致的树结构分裂。
利用第三步生成的CF Tree的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况
有序聚类
参考
https://www.cnblogs.com/yixuan-xu/p/6272208.html
https://blog.csdn.net/u014593570/article/details/77746904


