【学习】彻底理解树状数组

前言：
可能是因为学习了很多高级数据结构的缘故，突然感觉好像明白了树状数组，重新总结一下。
本文通过从根源深处挖掘树状数组所解决的问题，深刻的理解树状数组的操作本质，若要系统的研究树状数组，建议学习一下“二进制分解”“倍增”的概念。
考虑到初学者，文章写的比较长，废话比较多，还望耐心的看下去，相信你也能有新的收获。
温馨提示：文章中的代码仅供参考，虽然保证100%正确，但使用时请根据原题情况自行编写。

---

简介

树状数组是一种可以在 O(logn) 内完成区间 [1,n] 的可加性询问（求和，求乘积），在 O(logn) 内完成单点数据修改的数据结构（以上两种为基本的操作）。
它的代码量小，常数较小，但是不支持求区间最值（可以使用线段树）。

原理

其实树状数组的核心思想就是倍增，从根本上来说，树状数组是ST算法的强化版。
ST表主要处理的区间不可加性的问题，而与之类似的树状数组可以求得区间可加性问题。

请暂时忽略网上所流传的一些树状数组的写法，我们先从另一个角度理解一下。

朴素的倍增算法

设 sum[i][j] 表示从 i 开始向后 2j 个数的和，如果通过预处理得到这个数组，我们可以利用倍增算法求得任意一个 [l,r] 区间的和。

预处理：

void init(){
    for(int i = 1; i <= n; i ++) sum[i][0] = v[i];
    for(int j = 1; (1<for(int i = 1; i+(1<1 <= n; i ++)
            sum[i][j] = sum[i][j-1] + sum[i+(1<<(j-1))][j-1];
}

求 [l,r] 区间的和：

int que_sum(int l, int r){
    int res = 0;
    for(int i = MAXLOG; i >= 0; i --)
        if(l + (1<1 <= r) res += sum[l][i], l += (1<return res;
}

让我们计算一下复杂度：
时间复杂度： O((n+q)logn)
空间复杂度： O(nlogn)

这种方法的 logn 常数比较大，而且空间复杂度有些大，还有就是因为预处理的原因不支持修改操作，我们考虑改进。

优化1：对二进制数位操作

上面的算法无论询问的区间大小是多少，都要从MAXLOG开始循环到0，但对于比较小的数，是完全没有必要的。

当查询区间 [1,5] 时，其示意图如下图所示：

操作时，我们依此跳过上面的 1,2,3,4 这4段，跳出的距离分别是 8,4,2,1 ，它们分别是 23,22,21,20 。
也就是说 15=23+22+21+20 ，这就是15的二进制分解，在二进制中表达为 (1111)2 。

所以我们可以二进制拆分以后正着循环，进行优化。

int que_sum(int l, int r){
    int res = 0, x = r-l+1;
    for(int i = 1; x; x >>= 1, i ++)
        if(x&1) res += sum[l][i], l += (1<return res;
}

这种写法类似与快速幂，原理还是倍增。

优化2：引入lowbit优化

考虑一个数 129 ，它的二进制表示为 (10000001)2 ， 129=28+20 ，但是还是要枚举1…7的部分，然而因为系数是0，所以它们对答案并没有贡献（类似于计算 0×27 ），在if(x&1)就会被pass掉。
这里介绍一种常数优化： lowbit(x) ，它可以 O(1) 的直接调到我们需要的位置，在最坏的情况下，这样做的总复杂度依然是 logn 的。

int lowbit(int x){
    return (x)&(-x);
}

这个函数的实现原理与计算机补码有关，这里不再介绍。
这里说一下功能，有兴趣的话可以点击此处阅读维基百科原文。打不开的话，这里摘录下来了一部分。

定义一个lowbit函数，返回参数转为二进制后，最后一个1的位置所代表的数值。
例如，lowbit(34)的返回值将是2；而Lowbit(12)返回4；Lowbit(8)返回8。
将34转为二进制 (00100010)2 ，这里的”最后一个1”指的是从 20 位往前数，见到的第一个1，也就是 21 位上的1。

也就是说，这个函数可以返回最小的2的幂次。
例如：
lowbit((10000001)2)=(1)2
lowbit((10001000)2)=(1000)2
所以我们用两次计算就可以得到 129 的二进制分解。

int que_sum(int l, int r){
    int res = 0, x = r-l+1;
    for( ; x; x -= lowbit(x)){
        int t = lowbit(x);
        int add = (int)(log(t)/log(2)+0.01);
        res += sum[l][add], l += t;
    }
    return res;
}

我们姑且把里面的 log() 看成是 O(1) 的，这样程序会得到一个常数优化。

优化3：成型的树状数组

那么优化2的瓶颈又在什么地方呢？
不难发现，难点在于如何让l不断的向r跳，这并不好处理。
因为不同位置的区间，可能要求l向后跳不同多的长度，但是如果我们处理的是 [1,p] ，从1开始，p的二进制分解就是区间长度的二进制分解。
分解完了以后，考虑从p向1的方向跳，这样每个点都只需要记录从 [p,p−lowbit(p)+1] 这一段的信息即可，因为一个数的lowbit是唯一的，所以对于不同的数，每个数只维护一个信息就可以了，空间复杂度变成了 O(n) ，可以直接用一个一位数组进行储存。
每操作一次都会减去这个数2的最小次幂，使操作的规模不断缩小，执行下去就可以处理了。
而一个数的2的次幂最多有 logn 个，所以时间复杂度就是 O(logn)
比如:
15=(1111)2 ，通过lowbit分解，它可以变成4个数的和：
(1111)2=(1)2+(10)2+(100)2+(1000)2 ，然后我们分析这个倒着跳的过程。
减去15的最小的2的幂次 20 得到14。
减去14的最小的2的幂次 21 得到12。
减去12的最小的2的幂次 22 得到8。
减去8的最小的2的幂次 23 得到0。
所以答案就是15，14，12，8这4个点上的信息之和。
之后，区间操作可以使用差分，对于一个区间 [l,r] ，我们先处理区间 [1,l−1] ，在处理区间 [1,r] ，然后做减法，就可以得到答案。
对于修改的操作，每次修改一个点，我们只要更新有覆盖这个点的信息段就好了，找到下一个覆盖数字x的信息段的方法是 x+=lowbit(x) ，这样就可以把当前的最低位进位，那个数一定是覆盖修改点里面最小的，这样一直加到大于n就停止。
这个优化是树状数组对朴素倍增最根本的优化，因为二进制分解的唯一行，所以减少了维护的信息，使维护的信息支持修改，常数变的非常小。

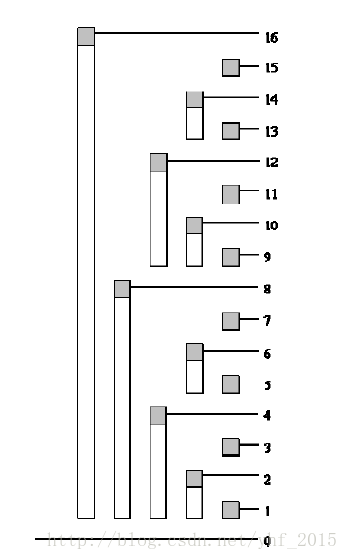
代码

int lowbit(int x){return x&(-x);}
int que_sum(int x){
    int sum = 0;
    for( ; x > 0; x -= lowbit(x)) sum += val[x];
    return sum;
}
void update(int x, int k){for( ; x <= n; x += lowbit(x)) val[x] += k;}

---

我的理解方式可能与大多数人不太一样，但是用这样的方式可以很好的体会树状数组的来源，深层度理解倍增算法，还希望对大家有帮助。
最后推荐一些博客：
int64Ago的专栏——搞懂树状数组
N3verL4nd——树状数组学习笔记