单通道语音增强之维纳滤波(二)
2.1 迭代维纳滤波算法简介
利用迭代思想去近似求解维纳滤波的非因果解,是用因果系统去实现非因果维纳滤波的一种方式。其基本思想为:先用带噪语音![]() 去初始化增强语音
去初始化增强语音![]() ,然后计算得到增益函数
,然后计算得到增益函数![]() ,并利用
,并利用![]() 对带噪语音
对带噪语音![]() 进行滤波,得到新的增强信号
进行滤波,得到新的增强信号![]() ,随后重复计算增益函数,再对带噪语音
,随后重复计算增益函数,再对带噪语音![]() 进行滤波,得到新的增强语音
进行滤波,得到新的增强语音![]() ,如此迭代数次后的增益函数值
,如此迭代数次后的增益函数值![]() 即为所求(这里的
即为所求(这里的 ![]() 表示迭代的次数)。
表示迭代的次数)。
接下来,介绍一下以迭代方式求解维纳滤波的几种具体算法。首先,针对是否添加约束条件,可以把迭代维纳滤波分成两大类:无约束的迭代维纳滤波和有约束的迭代维纳滤波。对于无约束的迭代维纳滤波方法,一种基于声道系统的全极点模型的估计方法是迭代维纳滤波中典型的代表,并且实验证明其性能也是相当不错的,后面我将对该算法进行详细的分析和实验。
2.2 全极点模型的无约束迭代维纳滤波算法
2.2.1 算法原理及步骤
语音可以被认为是声道这一线性时不变系统对周期性激励(浊音)和类随机激励(清音)的响应。那么,声道系统在z域就可以表示成如下的全极点形式:
其中,![]() 为系统增益,
为系统增益,![]() 为全极点系数,
为全极点系数,![]() 为全极点的个数。那么根据上述语音产生模型,我们便有了一种语音增强方法的新选择,即除了尝试估计纯净语音信号
为全极点的个数。那么根据上述语音产生模型,我们便有了一种语音增强方法的新选择,即除了尝试估计纯净语音信号![]() 自身以外,我们还可以估计用于产生该信号的参数。
自身以外,我们还可以估计用于产生该信号的参数。
算法的执行步骤如下:
1) 初始化:使用带噪信号来初始化信号的初始估计,即设![]() ,然后进行如下迭代,其中
,然后进行如下迭代,其中![]() 表示迭代次数。
表示迭代次数。
2) 在第![]() 次迭代中,对于给定的估计信号
次迭代中,对于给定的估计信号![]() ,利用线性预测技术(参考《语音增强理论与实践》维纳滤波与线性预测一节)计算全极点系数
,利用线性预测技术(参考《语音增强理论与实践》维纳滤波与线性预测一节)计算全极点系数![]() 。
。
3) 使用![]() 来估计增益项
来估计增益项![]() ,如下所示:
,如下所示:
其中,![]() 是步骤2)中估计出来的系数,而
是步骤2)中估计出来的系数,而![]() 为增益项的噪声方差,可表示如下:
为增益项的噪声方差,可表示如下:
其中![]() 是利用VAD(噪声活动性检测)在无语音帧计算得到的噪声功率谱估计。当然
是利用VAD(噪声活动性检测)在无语音帧计算得到的噪声功率谱估计。当然![]() 也可以采用其他噪声估计算法得到,例如最小值统计(MS)、最小值递归法(MCRA)等。针对单通道中噪声估计这一十分重要的问题,我会在以后的博客中单独介绍。
也可以采用其他噪声估计算法得到,例如最小值统计(MS)、最小值递归法(MCRA)等。针对单通道中噪声估计这一十分重要的问题,我会在以后的博客中单独介绍。
4) 计算信号![]() 的短时功率谱:
的短时功率谱:
5) 计算维纳滤波增益函数:
6) 估计增强后的信号谱:
其中,![]() 为带噪语音
为带噪语音![]() 的频谱。并对
的频谱。并对![]() 进行IDCT变换,便可以得到时域的增强信号
进行IDCT变换,便可以得到时域的增强信号![]() 。增益项的噪声方差
。增益项的噪声方差![]() ,可以计算如下:
,可以计算如下:
7) 回到步骤2),使用![]() 作为估计信号,重复上述步骤,直到满足收敛条件或者达到指定的迭代次数为止。
作为估计信号,重复上述步骤,直到满足收敛条件或者达到指定的迭代次数为止。
上述算法,便是Oppenheim和Lim,于1978年提出的全极点模型迭代的维纳滤波算法,在其算法中,他们使用了统计估计技术(最大后验估计)来估计带噪语音信号的全极点参数,考虑在给定带噪观测值![]() 和极点系数
和极点系数![]() 的情况下
的情况下![]() 的最大后验估计,即最大化条件概率密度
的最大后验估计,即最大化条件概率密度![]() 。算法的详细分析和推导过程,请查看《语音增强理论与实践》中迭代维纳滤波一节。
。算法的详细分析和推导过程,请查看《语音增强理论与实践》中迭代维纳滤波一节。
2.2.2 算法实验测试
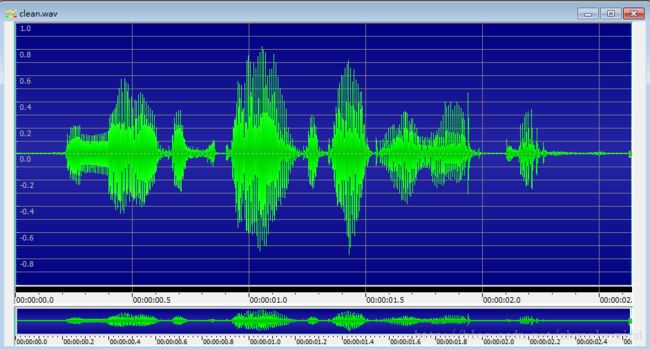
为了测试全极点模型的维纳滤波算法在语音降噪中的实际性能,我们进行如下实验:从NOIZEUS语音库中,摘取一段采样率为8kHz的纯净语音,并与白噪声混成0dB和15dB的两段带噪语音。利用算法进行迭代处理,迭代次数取5次(大多数情况下,3到7次就足够了),并利用GoldWave画出其时域波形图如下所示。
图一为纯净语音的时域波形图,图二是带噪语音及增强后语音的时域波形图,其中左上角为15dB的带噪语音,右上角为增强后的15dB带噪语音,左下角为0dB的带噪语音,右下角为增强后的0dB带噪语音。从上述时域波形图中,我们可以直观的看到,对于低信噪比的情况下(0dB带噪语音),噪音被衰减的同时,语音也被衰减,语音信号的幅度较纯净语音信号明显降低。并且,通过主观听音测试发现,增强后的0dB带噪语音含有明显地音乐噪声且语音失真较大。相反,在高信噪比的情况下(15dB带噪语音),语音恢复的比较完全,且没有音乐噪声,语音失真也很小。可见,这种全极点模型的无约束迭代算法,虽然在噪声环境极度恶劣的情况下的性能不尽人意,但是其应对一般的噪声环境的性能还是不错的。
2.3 有约束的迭代维纳滤波算法
有约束的迭代维纳滤波,其实就是在无约束的迭代算法中施加一定的约束条件,让最终迭代的结果满足事先施加的条件。其相关的算法,我已经在单通道语音增强之维纳滤波(一)中提及了三种,分别为:跨约束迭代的维纳滤波算法、基于码本的约束迭代维纳滤波算法和针对有色噪声的约束迭代维纳滤波算法。由于涉及的方法众多,且各自不同,这里就只简单介绍一下这三类方法的主要思想。
由于全极点的无约束迭代维纳滤波的全极点谱可能会产生形状不自然的谱峰,甚至产生伪峰,因此考虑通过施加约束的方式来解决,于是便有了两种算法:跨时间约束的迭代算法和跨迭代约束的算法。其中,跨时间约束的算法对频谱的连续性施加约束,以确保某一帧所得到的频谱于前一帧或后一帧的频谱差异不至于过大。但是,该方法需要用到未来帧的信息,所以它是非因果的,因此一般情况下,我们也不会采用。而在跨迭代的方法中,则考虑对迭代程度施加约束,以确保只产生有效的全极点谱,这种方法是因果的,可以实现的,所以便于用到工程中去。其主要思想,是对推导全极点系数![]() 的自相关系数施加一定的可变权重约束,使其在前几次迭代中,使用较大的权重,后几次迭代中,使用较小的权重,以此来保证较好的共振峰带宽和位置。
的自相关系数施加一定的可变权重约束,使其在前几次迭代中,使用较大的权重,后几次迭代中,使用较小的权重,以此来保证较好的共振峰带宽和位置。
基于码本的迭代约束维纳滤波算法,则是利用纯净语音的大数据库,预先训练好全极点系数的一个码本,然后在第 ![]() 次迭代中,使用最接近全极点系数
次迭代中,使用最接近全极点系数![]() 的码本系数
的码本系数![]() ,即满足如下条件:
,即满足如下条件:
其中,![]() 为码本的大小,
为码本的大小,![]() 表示Mahalanobis型的失真测度。此外,我们不仅可以利用纯净语音的码本,同样还可以利用噪声库的码本,这样的话还可以省去噪声估计算法,并且在非平稳噪声中也会取得很好的性能。但是,基于码本的算法也存在着一个很重要的缺点:码本搜索过程中引入的计算复杂度太高,不利于实时实现。因此,这也就是限制基于码本的算法不能普及的一个重要原因,但这种训练、搜索的方法,也启发了一些学者利用机器学习的方法进行语音增强,比如基于隐马尔科夫模型的语音增强方法,同样也是从训练库中搜索数据,实现匹配降噪。无论如何,这种思想还是非常重要的,只有新的思想,才会产生新的技术革新。
表示Mahalanobis型的失真测度。此外,我们不仅可以利用纯净语音的码本,同样还可以利用噪声库的码本,这样的话还可以省去噪声估计算法,并且在非平稳噪声中也会取得很好的性能。但是,基于码本的算法也存在着一个很重要的缺点:码本搜索过程中引入的计算复杂度太高,不利于实时实现。因此,这也就是限制基于码本的算法不能普及的一个重要原因,但这种训练、搜索的方法,也启发了一些学者利用机器学习的方法进行语音增强,比如基于隐马尔科夫模型的语音增强方法,同样也是从训练库中搜索数据,实现匹配降噪。无论如何,这种思想还是非常重要的,只有新的思想,才会产生新的技术革新。
最后,再介绍一种约束迭代的维纳滤波方法:针对有色噪声源的约束迭代维纳滤波算法。这种方法的思想很简单,由于有些噪声可能并不会像白噪声一样对语音的整个频谱产生影响,比如说汽车噪声,它只是对频谱的低频部分具有影响。因此,我们可以考虑设计一种算法,只针对频谱中的低频(或高频)进行约束,于是便有了这种针对有色噪声源的约束迭代维纳滤波算法。该算法的具体做法是先将信号频谱线性地划分成几个频带,然后对每个子带施加不同的迭代次数(迭代次数是根据每个子带受污染的程度而定)来实现对有色噪声源的降噪。
参考文献:
- 《语音增强理论与实践》(Loizou 2012)
- All-pole modeling of degraded speech. IEEE Trans. Acoust. , Speech, Signal Proc., ASSP-26(3), 197-210. (Lim, J. and Oppenheim, A. V. 1978)