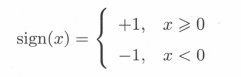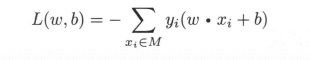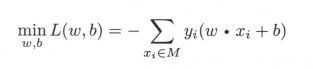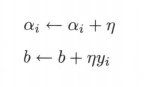感知机+Python3的实现（原始形式与对偶形式）
1. 什么是感知机？
感知机（perceptron）是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误差的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。感知机学习算法具有简答而易于实现的优点，分为原始形式和对偶形式，下文会一一给出。感知机预测是通过对训练数据的学习对新输入的实例进行分类。
定义1.1（感知机）
假设输入空间（特征空间）是
，输出空间是Y = {+1,-1}。输入
表示实例的特征向量。对应于输入空间（特征空间）的点；输出
表示实例的类别。由输入空间到输出空间的如下函数：
f(x) = sign(w*x+b)
称为感知机。其中，w和b为感知机模型参数，
叫作权值向量（weight vector）, 
叫作偏置（bias）,w·x表示w和x的内积。sign是符号函数，即
感知机是一种线性分类模型，属于判别模型。感知机模型的假设空间是定义在特征空间中的所有线性分类模型（linear classification model）或线性分类器（linear classifier）,即函数集合 { f |f(x) = w·x+b }。
感知机有如下几何解释：线性方程
w · x + b = 0
对于于特征空间
中的一个超平面S，其中w是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部的点（特征向量）分别分为正，负；两类。因此超平面S称为分离超平面（separating hyperplane）,如图所示
感知机学习，由训练数据集（实例的特征向量及类别）
其中，
，求得感知机模型，即求得模型参数w,b。感知机预测，通过学习得到的感知机模型，对于新的输入实例给出其对应的类别。那么感知机如何学习？确定w,b? 不要着急下文慢慢道来。
2. 感知机的学习策略
假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。为了找出这样的超平面，即确定感知机模型参数w，b，需要确定一个学习策略，即定义（经验）损失函数并将损失函数极小化。
损失函数的一个自然选择是误分类点的总数。但是，这样的损失函数不是参数w, b 的连续可导函数，不易优化。损失函数的另一个选择是误分类点到超平面S的总距离，这是感知机所采用的。为此首先写出输入空间
中任一点
到超平面S的距离：
这里，||w||是 w 的 L2 范数。
其次，对于误分类的数据
来说，
成立。因为当[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wIvb8tuj-1597766733096)(…/…/Library/Application%20Support/typora-user-images/image-20200818233851447.png)]时 ，
因此，误差分类点
到超平面S的距离是
这样，假设超平面 S 的误分类点集合为 M ，那么所有误分类点到超平面 S的总距离为
不考虑
，就得到感知机学习的损失函数。
给定训练数据集
其中，
。感知机 sign(w · x + b)学习的损失函数定义为
其中 M 为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。
显然，损失函数L(w，b）是非负的（误分类结果与正确分类符号相反）。
如果没有误分类点，损失函数值是0.而且，误分类点越少，误分类点离超平面越近，损失函数值就越小。一个特点的样本点的损失函数：在误分类时参数w,b的线性函数，在正确分类时是0。因此，给定训练数据集T，损失函数L(w,b) 是w , b 的连续可导函数。
2.1 感知机学习算法的原始形式
感知机学习算法是对以下最优化问题的算法。给定一个训练数据集
其中，
，求参数 w , b 使其为以下损失函数极小化问题的解
其中 M 为误分类点的集合。
感知机学习算法是误分类驱动的，具体采用随机梯度下降法(stochastic gradient descent) 。首先，任意选取一个超平面
,然后用梯度 下降法不断地极小化目标函数。极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。
假设误分类点集合M是固定的，那么损失函数 L( w, b )的梯度由
给出。
随机选取一个误分类点
，对 w, b进行更新：
式中
式步长，在统计学习中又称为学习率(learning rate)。通过迭代可以期待损失函数L( w, b)不断减小，知道为0。综上所诉，得到如下算法：
2.1.1 （感知机学习算法原始形式）
输入：训练数据集
，其中
；学习率[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fdGVsjlC-1597766733124)(/Users/jgl/Library/Application Support/typora-user-images/image-20200815111741891.png)]
输出：w, b; 感知机模型 f(x) = sign(w · x + b)。
(1)选取初值
；
(2)在训练数据集中选取数据
(3)如果
(4)转至(2),直到训练集中没有误分类点。
这种学习算法直观上有如下解释：当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整 w , b 值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面的距离，直到超平面越过该分类点使其被正确分类。
2.2 感知机学习算法的对偶形式
现在考虑感知机学习算法的对偶形式。
对偶形式的基本想法是，将 w 和 b 表示为实例
和标记
的线性组合的形式，通过求解其系数而求得 w 和 b。 不失一般性，假设初始值
均为0。对误分类点
通过
逐步修改 w, b，设修改 n 次，则 w , b 关于
的增量分别是
和
这里
这样，从学习过程不难看出，最后学习到的 w,b 可以表示为
这里，
时，表示第 i 个实例点由于误分而进行更新的次数。实例点更新次数越多，意味着它距离分离超平面越近，也就越难正确分类。换句话说，这样的实例对学习结果影响最大。
下面对照原始形式来叙述感知机学习算法的对偶形式。
算法 2.2 （感知机学习算法的对偶形式）
输入：线性可分的数据集
,其中
输出：a, b ;感知机模型
，其中 a = 
。
(1) a<-0 , b<-0;
(2) 在训练集中选取数据[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p6dUHfPj-1597766733153)(/Users/jgl/Library/Application Support/typora-user-images/image-20200815225403319.png)]
(3) 如果
，
!
(4) 转至（2）直到没有误分类数据。
对偶形式中训练实例仅以内积的形式出现。为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵形式存储，这个矩阵就是所谓的Gram矩阵
与原始形式一样感知机学习算法的对偶形式迭代是收敛的，存在多个解。
3. Python3实现
3.1 感知机原始形式
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:
def __init__(self):
self.w = np.ones(len(data[0]) - 1, dtype=np.float32)
self.b = 0
self.l_rate = 0.1
# 感知机模型
def sign(self, x1, w, b):
return np.dot(x1, w) + b
# 随机梯度下降法进行调整模型参数 w ,b
def fit(self, x_train, y_train):
is_wrong = False
while not is_wrong:
wrong_count = 0
# 寻找误分类点，并更新w,b
for i in range(len(x_train)):
x = x_train[i]
y = y_train[i]
# 满足y*(x*w+b)<=0则为误分类点
if y * self.sign(x, self.w, self.b) <= 0:
self.w = self.w + self.l_rate * np.dot(y, x)
self.b = self.b + self.l_rate * y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return 'ok'
if __name__ == '__main__':
# 本例子训练数据采用sklearn提供的自带的数据集-莺尾花数据集
# 对数据进行简单的处理，主要是运用pandas一些特性，可以参考我的另一篇博文
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, [0, 1, -1]])
x, y = data[:, :-1], data[:, -1]
# 对y值进行处理，因为感知机中y值只有-1，1
y = np.array([1 if i == 1 else -1 for i in y])
perceptron = Model()
perceptron.fit(x, y)
# 构造4-7范围内十个等差数列
x_points = np.linspace(4, 7, 10)
#print((perceptron.w[0] * x_points + perceptron.b))
# 求点到感知机平面的距离
y_ = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='red', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
3.2感知机对偶形式
import numpy as np
class Model:
def __init__(self):
self.a = np.zeros(3, dtype=np.float32)
self.b = 0
self.l_rate = 1
def fit(self, x_train, y_train):
is_wrong = False
while not is_wrong:
wrong_count = 0
for i in range(len(x_train)):
sum = 0
for j in range(len(x_train)):
sum += np.dot(x_train[j] * self.a[j], y_train[j])
sum = np.dot(sum, x_train[i]) + self.b
if y_train[i] * sum <= 0:
self.a[i] = self.a[i] + self.l_rate
self.b = self.b + self.l_rate * y_train[i]
print(self.a, self.b)
print("-----------------")
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return 'ok'
if __name__ == '__main__':
# 进行数据测试,查看每次参数的变化
x_train = np.array([(3, 3), (4, 3), (1, 1)])
y_train = np.array([1,1,-1])
per = Model()
per.fit(x_train,y_train)
4. 总结
-
感知机是根据输入实例的特征向 对其进行 类分类的线性分类模型:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zu5sWWfe-1597766733158)(/Users/jgl/Library/Application Support/typora-user-images/image-20200818135741608.png)]
感知机模型对应于输入空间(特征空间)中的分离超平面 w · x+b = 0。
-
感知机学习的策略是极小化损失函数:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ml6ztOSs-1597766733160)(/Users/jgl/Library/Application Support/typora-user-images/image-20200818140012575.png)]
损失函数对应于误分类点到分离超平面的总距离
-
感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形
式和对偶形式。算法简单且易于实现 原始形式中，首先任意选取 个超平面，然后
用梯度下降法不断极小化目标函数。在这个过程中一次随机选取 个误分类点使其梯
度下降。
如果你觉得这篇文章有收获就给我点个赞吧!
下期预告：朴素贝叶斯算法