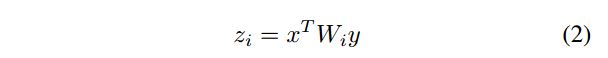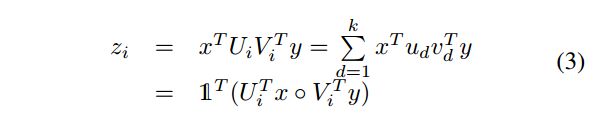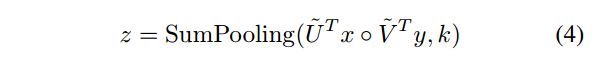【文献阅读】MFB——结合协同注意力的多模态矩阵分解的双线性池化方法（Z. Yu等人，ICCV，2017，有代码）

一、背景

文章题目：《Multi-modal Factorized Bilinear Pooling with Co-Attention Learning for Visual Question Answering》

MFB还是挺经典的一篇VQA文章。

文章下载地址：https://arxiv.org/pdf/1708.01471.pdf

文章引用格式：Zhou Yu, Jun Yu, Jianping Fan, Dacheng Tao. "Multi-modal Factorized Bilinear Pooling with Co-Attention Learning for Visual Question Answering." International Conference on Computer Vision (ICCV), 2017

项目地址：https://github.com/yuzcccc/mfb

二、文章摘要

Visual question answering (VQA) is challenging because it requires a simultaneous understanding of both the visual content of images and the textual content of questions. The approaches used to represent the images and questions in a fine-grained manner and questions and to fuse these multimodal features play key roles in performance. Bilinear pooling based models have been shown to outperform traditional linear models for VQA, but their high-dimensional representations and high computational complexity may seriously limit their applicability in practice. For multimodal feature fusion, here we develop a Multi-modal Factorized Bilinear (MFB) pooling approach to efficiently and effectively combine multi-modal features, which results in superior performance for VQA compared with other bilinear pooling approaches. For fine-grained image and question representation, we develop a ‘co-attention’ mechanism using an end-to-end deep network architecture to jointly learn both the image and question attentions. Combining the proposed MFB approach with co-attention learning in a new network architecture provides a unified model for VQA. Our experimental results demonstrate that the single MFB with co-attention model achieves new state-of-theart performance on the real-world VQA dataset. Code available at https://github.com/yuzcccc/mfb.

视觉问答需要同时理解图像内容和文本内容。现有的方法都是用精校正的方式表示图像和问题，然后再把多模态特征融合起来。基于双线性池化的模型较其他线性模型表现出较好的效果。但是这种方法的维度过高，计算量巨大限制了其应用。对于多模态融合，我们提出了一种多模态双线性矩阵分解池化方法（MFB），来准确有效的结合多模态特征，这比其他的双线性池化方法更优。对于精校正的图像的问题表达，我们提出一种协同注意力机制，能够端到端的用于深度网络中，同时学习图像和问题注意力。结合MFB和协同注意力到网络中，可设计出一个新的VQA模型。实验表明该模型在现有的VQA数据集上达到了最好的效果。

三、文章详细介绍

现有的VQA方法大概有三个阶段（1）将图像表征为视觉特征，将问题表征为文本特征（2）多模态融合（3）利用融合特征来学习分类器以预测最佳匹配答案。

传统的特征融合方法就是对应相加或者链接，但是这种线性融合方式不能表示出复杂的特征交互。而双线性池化方法是用于整合CNN提取出的图像特征，用于图像识别。但是这种方法输出的特征维度较高，并且计算量巨大，严重阻碍了其进一步应用。Fukui et al.等人提出了多模态紧凑型双线性池化方法（MCB），并获得了VQA challenge 2016的冠军。然而，MCB仍然需要高维来确保鲁棒性，为了解决这个问题, Kim et al.等人提出了一种多模态低秩双线性池化方法（MLB），它是基于矩阵的Hadamard product来计算两个特征向量的。MLB的维度低，且参数较少，不过其对参数非常敏感，收敛慢，因此本文提出了MFB，同时结合了MLB和MCB的优点。

关于特征表示，如果直接使用全局特征，则会引入许多无关噪声，因此使用注意力机制能够学到更多和问题相关的特征。然而，很多现有的方法只使用了图像注意力而没有使用文本注意力，因此作者基于MFB，使用了协同注意力学习机制，同时学习文本注意力和图像注意力。

因此这篇文章的主要贡献在于：

First, we develop a simple but effective Multi-modal Factorized Bilinear pooling (MFB) approach to fuse the visual features from images with the textual features from questions. MFB significantly outperforms existing multi-modal bilinear pooling approaches such as MCB [6] and MLB [12]. 提出了MFB双线性池化方法。

Second, based on the MFB module, a co-attention learning architecture is designed to jointly learn both image and question attention. Our MFB approach with co-attention model achieves the state-of-theart performance on the VQA dataset. 提出了协同注意力机制

We also conduct detailed and extensive experiments to show why our MFB approach is effective. Our experimental results demonstrate that normalization techniques are extremely important in bilinear models.在现有数据集上的实验表明该模型有效。

1. 相关工作

VQA：最早应该是Malinowski et al.的文章来尝试做VQA，VQA总体来说可以分为三类：粗联合嵌入模型；结合注意力的精联合嵌入模型；基于外部知识的模型。粗联合嵌入模型（coarse joint-embedding models）是最直接的模型，两个模态都表示为全局特征，然后整合在一起来预测答案。这类方法的限制就是全局特征可能存在噪声，使得其难以回答细致的问题。后来就又提出了一种结合注意力的精细联合嵌入模型（fine-grained joint-embedding models with attention），目前也有很多相关工作了，例如SAN，前面说到的MCB。

• M. Malinowski and M. Fritz. A multi-world approach to question answering about real-world scenes based on uncertain input. In Advances in neural information processing systems (NIPS), pages 1682–1690, 2014. 1, 2

用于VQA的双线性模型（Multi-modal Bilinear Models for VQA）：最常用的模态融合就是对应元素相加或者链接，然而这类方法表示出的特征是不够充分的。因此后来采用了双线性融合模型，比如MCB，MLB。

2. MFB（Multi-modal Factorized Bilinear Pooling）

公式推导这里就简单说一下，假如两个输入的模态分别是x和y，那么双线性融合就可以表示为：

W就是我们的投影矩阵，这里作者省略了偏置项，z是双线性模型的输出。

作者的灵感就是来源于矩阵分解，将W分解为两个低秩的U和V矩阵：

k就是分解矩阵的维度。◦表示矩阵点乘。

U和V本身是一个三维的张量，不失一般性（Without loss of generality），可以用reshape操作将其表示为二维数据，因此上式可以写作：

即在点积的结果上使用求和池化。池化窗口的大小为k。我们把这种方法称作矩阵分解双线性池化方法MFB。

MFB的具体细节如下图（a）所示：

MFB可以很容易的和其他层结合起来，比如池化层，全连接层，点积层。为了避免过拟合，可以在点积层后面添加dropout。因为引入了点积，输出的神经元也许会非常显著，模型或许会收敛到局部最小，因此在MFB的输出后可使用正则化，这里作者采用了power normalization或者l2范数normalization。MFB的结构如（b）中所示。

MFB和MLB的关系：MLB就是K=1时候的MFB的特殊情况，相当于秩为1的分解。

3. VQA的网络结构

VQA网络结构有两个，它们都是将VQA视作分类问题，一个是用了一个MFB模块的baseline，另一个是增加了协同注意力的模型。

（1）MFB Baseline

提取图像特征用的ResNet-152，输入图像大小为448×448，输出的2048维的pool5层结果。问题先用tokenized进行分词，然后转化为one hot向量，然后将one hot向量进行嵌入，并将嵌入结果输入到两层的LSTM中，每个单词得到1024维的特征。然后从每一层的最后一个单词的特征抽出，链接成2048维的问题表征。

之后将提取的问题表征和图像表征输入到MFB中，进行融合并预测最终答案。loss采用的是KL散度（KL-divergence loss），模型结构如下图所示：

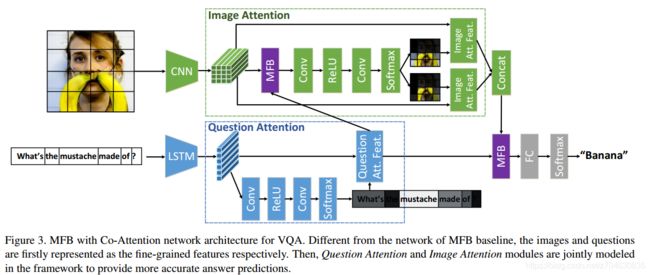
（2）MFB with Co-Attention

这里在之前模型的基础上增加了协同注意力。图像注意力采用了空间格网（spatial grid），取resnet-152输出的14×14的层，然后将这个图像特征与问题特征输入到MFB中进行融合，并使用了特征转换的技巧（比如1×1矩阵，ReLU激活）和softmax归一化来预测每个格网位置的注意力权重。生成的多重注意力图可以学习注意力映射，并将其与图像特征进行连接，最终再和问题特征同时输入到MFB中预测最终答案。

整个模型如下图所示：

相较于其他注意力模型，该模型的创新之处在于引入了文本的注意力模型。后文中作者将该模型记做MFB+CoAtt。

4. 实验

作者使用的数据集是VQA v1，实验参数就不介绍了。

（1）消融实验

首先比较MFB和MCB和MLB，结果如下图：

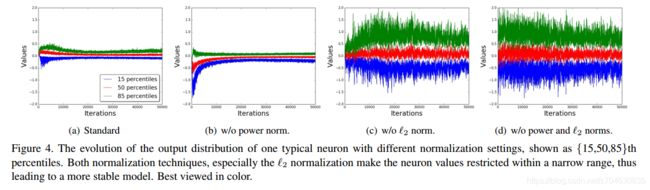
对于两种正则化方法，Power normalization获得了0.5%的性能提升，l2 normalization获得了3%的性能提升。为了说明为什么正则化重要，作者选取了正则化之前的MFB输出的随机神经元，进行了统计，结果如下图：

（2）与其他模型比较

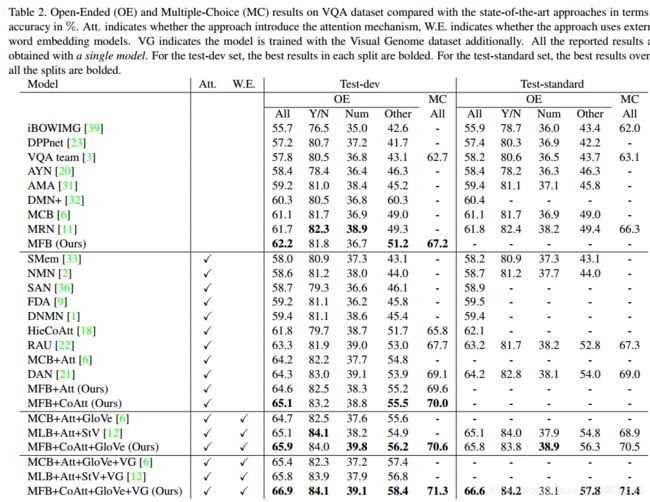
与其他模型比较的结果如下图所示：

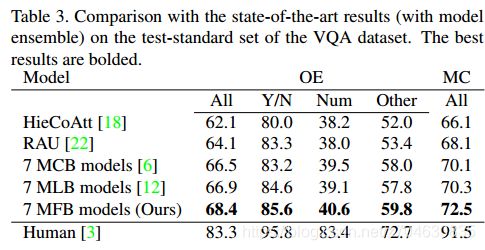
作者提出的方法与其他集成的方法比较结果如下：

最后是作者对模型的注意力结果的可视化：

四、小结