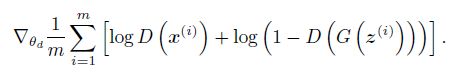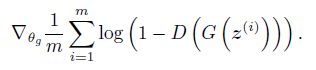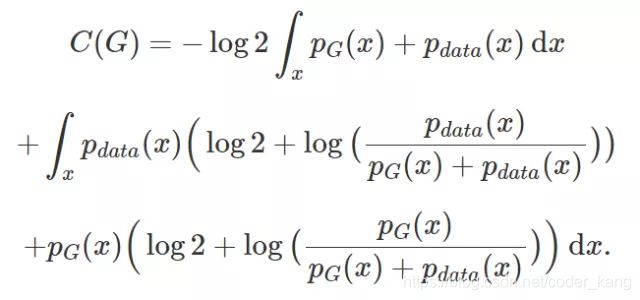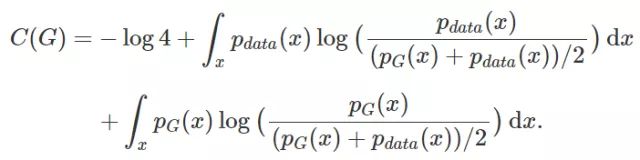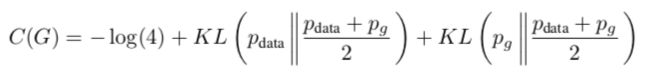生成对抗网络(GAN)论文原文详解
最近在学习生成对抗网络的相关知识,首先接触到的当然是Ian Goodfellow的原始论文,文章中作者很简要的阐明了GAN的基本算法,同时也给出该算法可行的理论证明。
该模型通俗点说,就是可以利用已知分布的数据对模型进行训练,训练完成后,该网络能够自动的生成与原始数据分布相似的数据。举例来说,给网络投喂熊猫的照片进行训练,训练完成后,网络会自动生成一组熊猫的照片。在今年的ICLR大会上,就有一篇关于GAN生成图像的文章,利用文章的算法生成的图像十分逼真,某些图片肉眼也很难分清差别。
上图是使用改造过后的GAN算法生成的,可谓是栩栩如生。GAN算法从14年发表到现在,短短五六年,接着深度学习的东风有了长足的发展。GAN的算法很简单,但是对其可行性的证明中用到一些概率相关的数学工具,需要好好的理解。本文中很多的观点是个人的理解,难免有很多的疏漏,希望大家可以在文章下留言指正。
1 生成模型与判别模型
与以往经典的机器学习算法相比,GAN算法最大的创新来自于结合了生成模型和判别模型,以二者的相互对抗进而相互优化。作者将GAN比喻为警察和假币制造者的一场零和博弈,最开始罪犯制造好假币,警察通过技术手段辨认出真伪,后罪犯提高假币的制造水准,警察的辨认能力也不断地提高。就在二者的相互博弈中,罪犯制造假币的能力不断提升,警察的辨认能力也达到了顶峰。这里的罪犯便是网络中的生成器,而警察则是模型中的判别器。
关于生成模型和判别模型不是文章的重点,Ian Goodfellow在原文中提到使用任何一种生成方法和判别方法都是可以的。但是了解生成模型和判别模型有何区别,有助于我们理解文章。
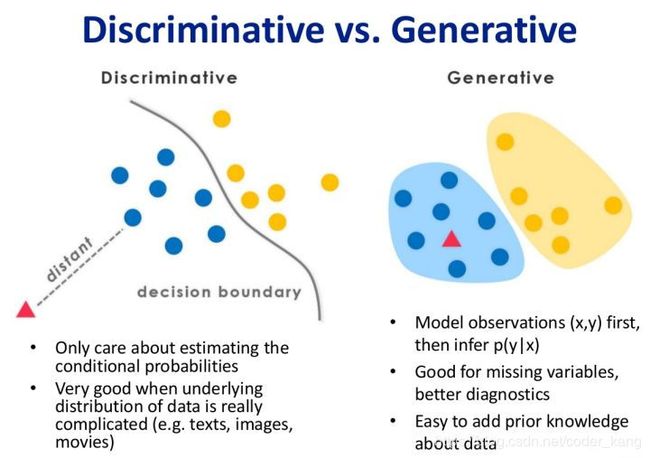
上图是生成模型与判别模型在机器学习中的值观体现,对于二分类问题,判别方法直接学习出决策函数(如左图的决策边界)或者条件概率,但是对于数据确切的分布情况的是未知的。例如我们熟悉的感知机、K近邻算法等。而生成方法则是学习数据的内在分布,通过概率判断分类。
总而言之,判别方法学习得到的是一个判断数据是否属于某一类的模型,而生成方法则学习到数据的分布。
而本文的关键就是生成一个与输入数据分布相似的分布,故核心就是训练一个好的生成器,而怎么训练呢又是一个问题。
2 模型实体
为了让大家对整个模型有个值观的印象,给出是Ian Goodfellow演讲PPT中的一张图,图中左下方的网络便是生成器,右上角的是判别器。我们现在无需考虑网络的内部结构,以及如何生成假的样本或是判别真假样本,这些是对应的模型该做的事情,我们将其看作一个使用误差反向传播算法的黑箱即可。
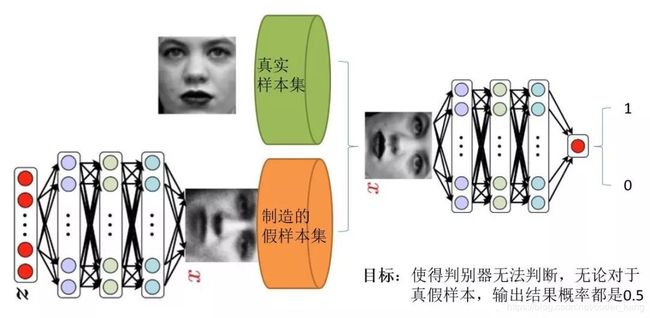
判别器训练
1.对生成器输入一段噪音,输出一个符合某一分布的假数据(如一组图片的分布);
2.从生成的分布中抽取一些数据,标记为0,从真实样本集中抽取一些数据,标记为1;
3.将数据喂给判别器进行训练,使判别器能够很好的分辨数据的真伪,判别器训练完成
训练器训练
4.将生成器与判别器进行逻辑连接,生成器产生的假数据全部标记为1喂给判别器;
5.喂给网络的数据产生的误差,通过误差反向传播算法传递给训练器,修正生成器的参数
(此处为GAN算法的精妙之处,生成器与判别器是逻辑相连,误差仅仅修正生成器而不改变判别器的参数)
6.不断训练判别器和生成器,直到判别器无法分辨假数据和真实数据,即判别器输出结果的概率都是0.5
3 训练算法
3.1 算法
原文章给了一个很经典的数学公式,虽然很好理解,但是其中的数学原理却没有那么简单。让我们先从算法本身开始,现在我们已经对整个网络有了个大致直观的认识,就是两个神经网络的相互连接,相互对抗优化。神经网络中除了模型本身如网络规模的选择、激活函数的选择等,很重要的一点就是损失函数,损失函数决定着这个网络要训练成为一个什么模样,下图给出了GAN的算法。
3.2 损失函数
算法的过程和2中描述的算法类似,其核心就是被优化的函数,在判别起的优化中,用到的是:
这个损失函数是不是很眼熟?对,就是我们在神经网络及逻辑斯蒂回归中常用的对数损失函数,在输入服从0-1分布时,损失函数如下:
![]()
在算法中,D(x)为生成器,输入一些数据,输出结果为真的概率,而G(z)则输入一些数据,产生一些符合D(x)输入的特定分布的数据。x(i)为真实数据,标记为1,G(z(i))为生成器创造的假数据,标记为0。
由于对数损失函数是很经典的损失函数,本文就不再赘述,但是可以很明显的发现,在二分类问题上的对数损失函数,若标签为1,则后半部分为零,若标签为0,则前半部分为零。因此文中给定的损失函数,就是等价于对数损失函数。由于对数损失函数良好的数学特性,可以通过梯度下降数法等优化算法很快的最小化损失函数。
注意,文中给定的损失函数和对数损失函数相差一个负号,因此就变成了最大化损失函数,实质都是一样的,只是为了数写的统一性。
而对于生成器,文中给出的损失函数如下:
在优化生成器时,我们将G(z(i))输出的结果,全部标记为1放入D(x)即判别器中,实质的误差由判别器产生,只是将误差传递给生成器用以修正参数。所以我们还是使用二分类问题的对数损失函数.
但是这里就会有人奇怪,按照对数损失函数,正例不应该log(D(G(z(i))))吗?其实是一样的,此处是要最大化D(G(z(i))),让其最大限度的接近1,也等价于最小化log(1-D(G(z(i))))。作者这样做也只有一个目的,就是让公式更加优美。
3.3 优化策略
到这里,我们对整个网络的对抗过程已经有了一定的了解,但是要让他们对抗起来,又是个问题。假如判别器一次性优化到最优,那么再优化生成器的时候就会很难,因此我们需要进一步优化其学习过程,可以慢慢的进行修正,例如可以判别器梯度下降K次,然后生成器下降一次。
这里就不得不提一点关于判别模型和生成模型的性质。生成模型,由于直接学习的数据的联合概率分布,收敛较快,但是判别模型直接学习决策函数之类,需要不断的迭代优化,收敛较慢。因此我么使用判别器梯度下降K次,然后生成器下降一次的方法来解决二者的对抗匹配问题。
很多朋友再这里可能都会有误解,为什么不一次性优化到最好呢?首先是模型上,我们的目的不是为了最优的判别器或者生成器,而是两者都很强大。在数学上的问题是当判别器优化到收敛后,梯度已经接近于零,再生成器优化器就很难优化了。
4. 数学思想
对于其数学内涵,可以看一看李宏毅老师对GAN的推导过程,讲的十分的仔细。对于网络,我们的目标是利用生成器生成一个与已知数据分布接近的数据分布,但是这具体是什么分布我们是未知的。例如给定的数据分布是一类图片的分布,我们进行形式化的描述的,但是我们可以生成一个和他近似的分布。
这里很容易让人迷糊的,是分布这个东西,在我们一般的经典机器学习算法中,往往使用的是判别方法,例如感知机、K近邻等,都只用分开数据,而不用考察数据本身的性质。但是生成方法就需要用到数据本身了。
文中给出了模型需要优化的值函数:
值函数优化目标分为两块,首先优化判别器,使之达到最大,此时生成器G(z)是固定的。再优化生成器,由于前一项中无生成器,所以直接优化后一项。有了上算法知识,应该很好理解这个值函数。
但是此处用到了期望,原因是说有的数据都是从某个分布中抽样出来的,我们无法例举所有的数据,只能采用采样的方式计算样本的期望。那么问题就来了,为什么优化这个函数,就能使我们的生成器生成的数据分布和真实的数据分布相似?
4.1 最优判别器
首先我们对V(D, G)展开:
pdata(x)和pG(x)分别代表原始数据和生成数据的概率密度,利用连续型随机变量的函数期望公式可得上式,同时利用换元法综合两个式子。第一步我们要最大化V(D, G),就等价于最大化:
上公式中对D(x)进行求导并令其等于零(注意此处我们在优化D(x)而非x,我们可以得出上式最优解为:
4.2 最优生成器
得到最优生成器后,我们将D*G代入V(D, G)中,再优化D,得C(G)
下面的一些技巧就需要些数学能力了,我们可以猜一下在如果给定的V(D, G)可用与衡量这个模型的优劣,那么最终在什么情况,会达到全局最优?肯定就是pdata(x)和pG(x)相等的情况(但是我们需要证明,此处仅仅是猜想),若两者相等,我们可以求的全局最小值为-log4。
有了这个简答的猜想后,我们就可以对我们现在的公式进行变形,目标是凑出一个-log4
由于pdata(x)与pG(x)之和的积分为2,我们的式子可以化简为:
同时我们引进一个KL散度和JSP散度的概念,在GAN中,这两个工具是很重要的,但是我们只需要知道,这个数学工具,可以用来衡量两个分布之间的相似度即可,两个分布的相似度越大,值越小,当相同时,值为0。这也和我们模型构建的目标相同,需要衡量生成的分布和真实的分布的相似度。
KL散度再转化为JSP散度,
![]()
经过数学变换C(G)变成了如上的式子,当pdata=pg时,C(G)最小,取-log4
故可知对于给定的式子的优化V(G, D)的优化,能够使得最终pdata=pg,即生成的分布与真实数据分布是相似的。
4.3 从数学模型到实际训练
但在实践中,我们是没有办法利用积分求这两个数学期望的,所以一般我们能从无穷的真实数据和无穷的生成器中做采样以逼近真实的数学期望。
这是机器之心的文章中对二者不同的解释,即数学期望是很复杂的,很难通过类似梯度下降算法的迭代对其进行优化,所以我们对其进行抽样以毕竟真实的数学期望。
5 总结
总而言之,该模型的核心思想就是利用一个生成器,一个判别器相互对抗、相互优化的过程。文章中还有实验部分及与其他算法比较的部分,因为不是算法的核心就略过了,最近几年GAN发展可以说是相当的迅速,各类算法层出不穷,可以很轻易的再github搜索到相关的项目。
6 参考文献
生成对抗网络原论文:https://arxiv.org/pdf/1406.2661.pdf
机器之心:GAN完整理论推导与实现 https://www.jiqizhixin.com/articles/2017-10-1-1