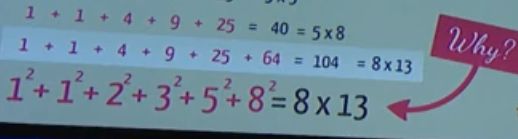作者前言
大家好,我是阿濠,今篇内容跟大家分享的是查找算法之斐波那契(黄金分割法)查找,很高兴分享到segmentfault与大家一起学习交流,初次见面请大家多多关照,一起学习进步.
一、斐波那契数列介绍
被我们称为"斐波拉契"的人,真实姓名叫列昂纳多,来自比萨,这个数列出自他的书《算盘宝典》("Liber Abaci"),这本书奠定西方世界的数学基础,其中的算法方法一直沿用至今
什么是斐波那契数列?
斐波那契数列指的是这样一个数列: 0, 1, 1, 2, 3, 5, 8, 13, 21....
特别指出:第0项是0,第1项是第一个1
这个数列从第三项开始,每一项都等于前两项之和。
斐波那契公式:F(k)=F(k-1)+F(k-2) 提示:F(1)=1 F(2)=1
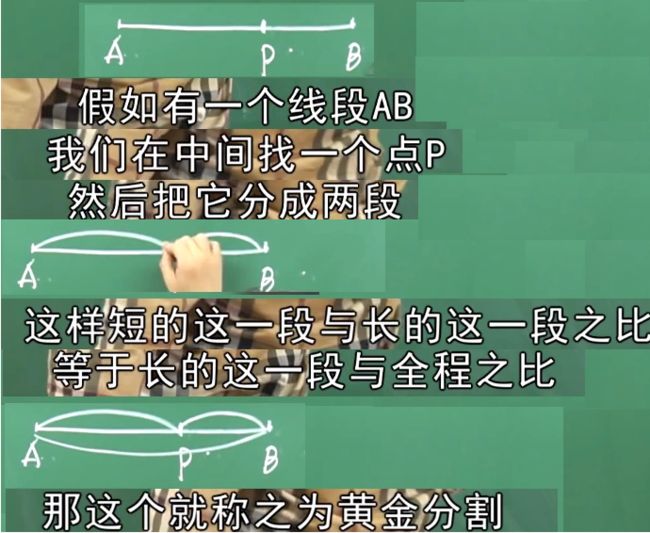
初识美丽漂亮的黄金分割
黄金分割点是把一条线段分割为两部分,其中一部分与全长之比等于另一部分与这部分之比。
由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。
取其前三位数字的近似值是618,这是一个神奇的数字,会带来意向不大的效果。
如果用大的斐波那契数 / 小的斐波那契数,也会发现越来越接近618
二、斐波那契(黄金分割法)查找算法介绍
基本原理
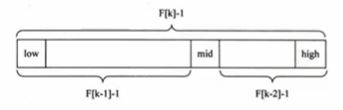
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,即mid=low+F(k-1)-1 (F代表斐波那契数列)
对F(k-1)-1的理解:
1.根据公式: F[k] = F[k-1] + F[k-2],得到(F[k]-1) = (F[k-1]-1) + (F[k-2]-1) +1
2.因为有时候顺序表长度 n 不一定刚好等于 F[k]-1 ,将原数组查找表扩展为长度为F[k]-1 (如果要补充元素,则补充重复最后一个元素,直到满足F[k]-1个元素),完成后进行斐波那契分割。
3.如图所示,只要顺序表的长度为 F[k]-1 就可以分割为前半部分F[k-1]-1]个元素,后半部分 F[k-2]-1 个元素,从而确定中间位置为 mid = low+F(k-1)-1,找出要查找的元素在那一部分并递归,直到找到。
为什么(F[k]-1) = (F[k-1]-1) + (F[k-2]-1) +1 ?
因为根据公式得出:F[k] = F[k-1] + F[k-2],而斐波那契数列是指:{1,1,2,3,5,8, 13...}
若此时 k = 4 ,则代入公式:F[4] = F[4-1] + F[4-2],求出数列F[4] 结果:5
若此时代入(F[k]-1),那么本来 求F[4] 就变成求 (F[4]-1) 结果就是f[4] - 1 = 5 - 1 = 4
公式代入则是:(F[4]-1) = (F[4-1]-1) + (F[4-2]-1) 也就是(F[4]-1) = (F[3]-1) + (F[2]-1)
摊开来将F[4]=5、F[3]=3、F[2]=1 代入:(5-1) = (3-1) + (2-1) 此时再 + 1 就相等了
三、通过应用示例认识斐波那契查找算法
对有序数组arr={1,8,10,89,1000,1234},进行斐波那契查找,输入一数看看该数组是否存在此数,存在则求出下标,如果没有就返回-1 表示没有这个数
//因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列
//因此我们需要先获取到一个斐波那契数列
//非递归方法得到一个斐波那契数列
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for(int i=2;i f[k] - 1) {
k++;
}
//如果要补充元素,则补充重复最后一个元素,直到满足F[k]-1个元素
int[] temp = Arrays.copyOf(arr, f[k]);//此时 k =5 f[5]=8
//因为arr[hight]代表最后一个元素,新数组temp = Arrays.copyOf(arr,f[k]);
//所以若想最后元素当作填充元素就应该是从hight + 1 开始
for (int i = hight + 1; i < temp.length; i++) {
temp[i] = arr[hight];
}
while (low <= hight) {
//按图所示进行黄金分割前部分+后部分
mid = low + f[k - 1] - 1;
//如果需要找的值key 小于temp[mid]说明我们应该继续向数组的前面查找(左边)
if (key < temp[mid]) {
hight = mid - 1;//往前缩范围
//为什么是k--
//1.全部元素= 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//之前(F[k]-1) = (F[k-1]-1) + (F[k-2]-1) +1
//按图所示,目前我们这里是mid= low + f[k - 1] -1;
//如果继续向数组的前面查找(左边)则应该是(F[k-1]-1)进行拆分
//(F[k-1]-1)=(F[k-1-1]-1) + (F[k-2-2]-1) +1 = 4 = 2 + 1 + 1
//即在f[k-1]-1 的前面继续查找k--
//即下次循环mid = f[k-1-1] -1
k--;
}
//我们应该继续向数组的后面查找(右边)
if (key > temp[mid]) {
low = mid + 1;
//为什么是k -=2
//1. f[k] = f[k-1] + f[k-2] .
//2.因为后面我们有f[k-2],所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
//3.即在f[k-2]的前面进行查找k -=2,即下次循环mid = f[k -1 - 2] -1
k -= 2;
}
if (key == temp[mid]) {
//因为之前如果要补充元素,则补充重复最后一个元素,直到满足F[k]-1个元素
//如果小于hight代表是arr数组里的值
if (mid <= hight) {
return mid;
} else {
//否则说明查找得到的数据元素是temp数组里的补充值
return hight;
}
}
}
return -1;
} 如果存在则求出下标,如果没有就返回-1表示没有这个数
执行代码测试一下数据看看,点击这里运行代码
四、算法复杂度分析
斐波那契查找的时间复杂度是:O(log 2 n )
与二分法折半查找相比,斐波那契查找的优点是它只涉及加法和减法运算,而不用除法,而除法比加减法要占用更多的时间,因此,斐波那契查找的运行时间理论上比折半查找小,但是具体还是得视具体情况而定。
五、斐波那契数列的有趣知识
计算中的斐波那契数列
让我们计算一下,头几个斐波那契数列的平方
毫无意外的,当你加上两个连续的斐波那契的数字时,你会得到下一个斐波那契数,但是也许你不知道把斐波那契数的平方,加起来会有什么有意思的结果?
没错,规律还在~事实上,还有一个规律,你计算一下头几个斐波那契数列的平方和
你可能觉得它们不是斐波那契数,但是如果你看的够仔细,会发现背后隐藏着斐波那契数
那么你就会发现1 、1 、2 、3 、5 、8的各平方加起来 = 104 = 8x13 why?
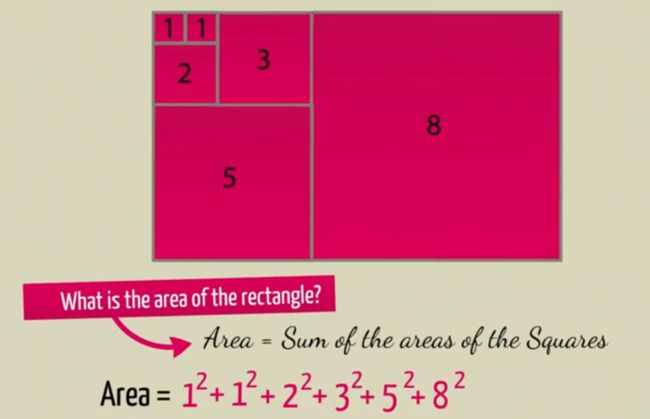
用一个简单的图形解答一下,先让我们画一个1 乘 1 的方块
现在问大家一个问题:这个矩形的面积是多少?
一方面它的面积是:组成它的小矩形之和
一方面因为是矩形,它的面积:长 * 高
所以这就是为什么1 、1 、2 、3 、5 、8的各平方加起来 = 104 = 8x13
黄金矩形与黄金螺旋
通过上面的知识点了解了黄金分割线,那么我们来再了解一下黄金矩形与黄金螺旋
生活中的斐波那契
斐波那契数列在自然界中神奇的出现,一朵花的花瓣数量、向日葵的螺旋,菠萝上表面的凸起,一般都对应着某个斐波那契数列
简单的说,植物的生长点每个一个角度就会发展出一个侧芽,如果这个侧芽角度太过平庸,新芽旋转几周后之后就会与老的侧芽对在一起,即浪费空间又争夺资源