3D Math Keynote
【3DMathKeynote】
1、常用公式。
1)(A*B)^T = B^T*A^T。
2)(A*B)^-1 = B^-1*A^-1。
3)|A*B| = |A|*|B|。
4)|M^T|=|M|
2、为什么矩阵的每一行可以解释为坐标系的基向量?
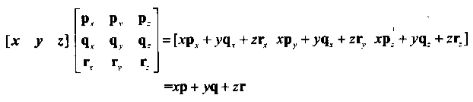
3、为了将原坐标系转换到新坐标系,用它乘以一个矩阵。
4、矩阵乘法的每一项C(i,j) = a(i,k)*b(k,j),k=1...n。
5、矩阵的行列式记为det M,或为|M|。假设矩阵M有r行、c列。记法M{ij}表示从M中除去第i行和第j列后剩下的矩阵,M{ij}称作M的余子式。M{ij}再乘上一个(-1)^(i+j),就叫作代数余子式。mij*Mij即为行列式。
6、det A^T = det A。
7、矩阵的标准伴随矩阵记为adj M,定义为M的代数余子式矩阵的转置矩阵。
8、矩阵的逆记为M^-1,可以用标准伴随矩阵除/矩阵行列式。只有方阵有逆矩阵。
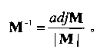
9、如果一组向量互相垂直,这线向量就被认为是正交基(othogonal basis)。如果它们都是单位向量,则称它们为标准正交基(orthonormal basis)。
10、直线方程可表示为P(x,y)N(a,b)=d,即ax+by=d。N是垂直于直线的单位向量,d给出了原点到直线的有符号距离。参考12.2.3。(x,y)的集合表示所有在N上投影长度为d的向量(或点)。
11、球的表面积:S=4*pi*r^2,不过的体积:V=4/3*pi*r^3。
12、AABB,axially aligned bounding box,轴对齐边界框。OBB,oriented bounding box,方向矩形边界框。
13、AABB比边界球更好的一个原因是,球只有一个自由度:半径。而AABB却有三个自由度:长、宽、高。
14、矩阵正交化的施密特算法:对每一行,从中减去它平行于已处理过的行的部分。
15、4D向量中的W分量能够开关4x4矩阵的平移部分。
16、圆函数:x^2+y^2+z^2=1。 x(t)=cos(2*pi*t),y(t)=sin(2*pi*t)。
17、射线:p(t)=p0+td。
18、通过计算三角形重心坐标,可以判断点是否在三角形内。三角形的重心是三个顶点的几何均值。
19、向量叉乘不满足交换律,它满足反交换律:a x b = - (b x a)。叉乘也不满足结合律。一般而方,(a x b) x c != a x (b X c)。