《零知识证明 – zkSNARK 入门》— PPIO Code Talks 第二期

PPIO Code Talks 致力于打造一个以上海为中心，辐射全球的高质量区块链学习，分享，交友平台。

7月27日，PPIO 举办了第二期 Code Talks 闭门技术交流分享会。在上一期的活动中，我们分享了两个前沿技术主题《Tindermint 介绍及实战分析》和《Libra 介绍及对 PPIO 的启发》。

这一期是我们 Code Talks 的第二期活动，我们有幸邀请到 Trapdoor CEO Star.LI 老师和 技术大咖王伯洋老师，两位重量级嘉宾来做主题分享。本期分享的主题是：1、《零知识证明–zkSNARK入门》， 2、《数字货币交易所架构初探》。两位老师分享的内容可谓干货满满，在本期文章中，我们先向大家介绍由Trapdoor CEO Star.LI 老师带来的《零知识证明–zkSNARK入门》主题分享和现场交流情。

在介绍零知识证明的技术细节之前，我们先来回顾一下零知识证明的历史
1985年 Zero-Knowledge Proofs [GMR85]
1992 年 Succinct ZK[K92]
2013 年 Pinocchio (PGHR13)
2016 年 Groth16
2017 年 Bulletproofs (BBBPWM17)
2018 年 zk-STARKs (BBHR18)
零知识证明，最早可以追溯到1985年的 Zero-Knowledge Proofs [GMR85] 创始论文。随后1992 年提出了精简的 ZK[K92] 证明。到了2013 年，零知识证明已经可以在现实生活中使用，但是速度较慢。2016 年的时候，Groth 提出了 Groth16算法，证明计算量被大幅度减少，从此，零知识证明开始逐步被真正的商用化落地。随后推出的 Bulletproofs 和 zk-STARKs，与 Groth16 被认为是目前主流的三个证明协议。
什么是“零知识证明”？

我们从事区块链开发的朋友们经常会听到“零知识证明”这样一个概念。那么究竟什么是零知识证明？如何去理解零知识证明？如果去运用它？
我们先通过一个“阿里巴巴零知识证明”小故事，来通俗解释一下什么是零知识证明。
阿里巴巴被强盗抓住，为了保命，他需要向强盗证明自己拥有打开石门的密码，同时又不能把密码告诉强盗。他想出一个解决办法，先让强盗离开自己一箭之地，距离足够远让强盗无法听到口令，同时又足够近让阿里巴巴无法在强盗的弓箭下逃生。阿里巴巴就在这个距离下向强盗展示了石门的打开和关闭。
这个整个过程就是零知识证明，证明者能够在不向验证者提供任何有用信息（石门的口令）的情况下，使验证者相信某个论断（阿里巴巴知道打开石门的方法）是正确的。

现在我们来详细解释一下，零知识证明（zh-SNARK）是 zero-knowledge Succint Non-interactive ARguments of Knowledge 的缩写。其中：

Zero Knowledge：证明者不泄漏欲证明的隐私信息

Succinct：证明的数据量比较小

Non-interactive：没有或者只有很少交互。

ARguments：计算可靠性下的证明。验证者只对计算能力有限的证明者有效。拥有足够计算能力的证明者可以伪造证明。这也叫“计算可靠性"（相对的还有”完美可靠性"）。

of Knowledge：对于证明者来说在不知道证据（Witness，比如一个哈希函数的输入或者一个确定 Merkle-tree 节点的路径）的情况下，构造出一组参数和证明是不可能的。

“零知识证明”是如何工作的？

如果要使用 zk-SNARK 零知识证明，就要首先将要证明的东西形成一个计算，并用计算电路表达出来，最后生成 QAP。零知识证明，最重要的一个逻辑就是 QAP。

零知识证明的工作流程主要分为4步：
首先将欲证明的计算性问题，转换成门电路 Circuit

然后将门电路 Circuit 转换成 R1CS

再将 R1CS 转变成 QAP

最后，基于 QAP 实现 zkSNARK 的算法

前面三步可以预先一次性完成，真正的证明过程主要是在第4步。

什么是QAP？

QAP 是 Quadratic Arithmetic Program 的缩写。在理解 QAP 之前，我们先来了解一下什么是 P 问题。

P 问题，也就是我们通常说的 在多项式时间内可解的问题。而与之相对的是 NP 问题。
NP 问题，也就是多项式时间内不可解，但是给定一个解，可以在多项式时间内验证这个解是否正确。
NPC 问题，也就是 NP 问题的核心，任何 NP 问题都可以归为到一个 NPC 问题。如果某个 NP 问题的 NPC 问题解决了，那么也就意味着原 NP 问题也解决了。
而我们今天谈的 QAP 问题，其实是 NP 问题。也是说 QAP问题可以在多项式时间内验证一个解是否正确，但在一个有限的时间内，使用有限的资源是很难在多项式时间内推出一个正确的解的。

如何验证一个 QAP 问题的解？
QAP 问题涉及到三组多项式：
[v0(x) , v1(x), v2(x), … , vm(x) ]
[w0(x) , w1(x), w2(x), … , wm(x) ]
[y0(x) , y1(x), y2(x), … , ym(x) ]
和一个目标多项式
t(x)=(x-1)(x-2)…(x-d)，其中 d 为电路门的个数
如果给定证据
u = [a1, a2, … , am]
能够使得多项式
(v0(x) + a1v1(x) + a2v2(x) +…+amvm(x))·(w0(x) + a1w1(x) + a2w2(x) +…+amwm(x)) - (w0(x) + a1y1(x) + a2y2(x) +…+amym(x))
能够被 t(x) 整除，则 u 是 QAP 问题的一个解

那么如何将一个普通的计算性问题转变成 QAP 问题呢？

首先，我们将计算性问题 “拍平(Flattening)”，使之变成一个个电路，例如 x3 + x + 5，我们可以将其拍平成 4 个电路
sym1 = x * x
y = sym1 * x
sym2 = y + x
out = sym2 + 5
其中 sym1, sym2 以及 y，是整个计算过程中用的临时变量，而 out 则为计算过程的最终输出结果。

接着，我们将电路转换成 R1CS 形式。
我们先将所有电路中出现的变量放到一个向量 s 里，并且再加上一个常数 one，也就是 1。
s = [one, x, out, sym1, y, sym2]
紧接着针对每个门我们开始变换。
例如 针对门 sym1 = x * x，我们可以将其看成是 x * x - sym1 = 0

其中：
x = [one, x, out, sym1, y, sym2] · [0, 1, 0, 0, 0, 0] = s · [0, 1, 0, 0, 0, 0]
sym1 = [one, x, out, sym1, y, sym2] · [0, 1, 0, 0, 0, 0] = s · [0, 0, 0, 1, 0, 0]
那 sym1 = x * x，我们就可以表示成
(s · [0, 1, 0, 0, 0, 0]) * (s · [0, 1, 0, 0, 0, 0]) - s · [0, 0, 0, 1, 0, 0] = 0 （I）
类似的，我们可以将 其他三个 门都表示成这种形式，他们分别是：
y = sym1 * x
sym2 = y + x
out = sym2 + 5
(s · [0, 0, 0, 1, 0, 0]) * (s · [0, 1, 0, 0, 0, 0]) - s · [0, 0, 0, 0, 1, 0] = 0 （II）
(s · [0, 1, 0, 0, 1, 0]) * (s · [1, 0, 0, 0, 0, 0]) - s · [0, 0, 0, 0, 0, 1] = 0 （III）
(s · [5, 0, 0, 0, 0, 1]) * (s · [1, 0, 0, 0, 0, 0]) - s · [0, 0, 1, 0, 0, 0] = 0 （IV）
我们把上述 （I）、（II）、（III）、（IV）四个式子中的 三个个向量分别用 A，B，C来表示

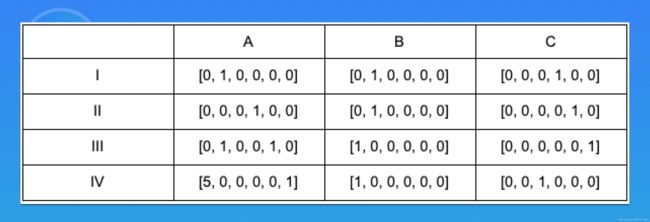
我们可以看到 A，B，C 的向量组的值，只和计算问题相关，而与问题的解无关。而此时 A、B、C向量组就构成了 R1CS。

更进一步的，我们把门电路编上号，第一个门编号为1，第二个门编号为2，依次类推。并且把向量组 A，看成是一个向量函数 A(x) = [A0(x), A1(x), A2(x), A3(x), A4(x), A5(x)]，其中 x 第门的编号。
那么，A0(x) 就相当于 是一个通过 (1,0),(2,0),(3,0),(4,0）这四个点的一个3次多项式。
如何得到这个多项式呢？答案是可以采用拉格朗日插值法。这样我们就可以求出 A0(x)
类似的，我们可以求出 A1(x), A2(x),…, B0(x), B1(x), B2(x),…, C0(x), C1(x), C2(x),…
这样我们就得到了关于x多项式的 A、B、C 向量
A(x) = [A0(x), A1(x), A2(x), A3(x), A4(x), A5(x)]
B(x) = [B0(x), B1(x), B2(x), B3(x), B4(x), B5(x)]
C(x) = [C0(x), C1(x), C2(x), C3(x), C4(x), C5(x)]
很显然如果 P(x) = (s · A(x))(s · B(x)) - s · C(x) 这个多项式在 x=1,2,3,4时都为0，则意味着原4个门电路都成立，也就等价于证明了 s 是原问题的解。
如果 P(x) = (s · A(x))(s · B(x)) - s · C(x) 在 x=1,2,3,4时都为0，等价于 P(x) 可以被 (x-1)(x-2)(x-3)(x-4)整除。
因此，证明者只需要证明自己拥有某 s，使得 P(x) 被 (x-1)(x-2)(x-3)(x-4)整除即可。
实际证明过程中，并不需要测试所有的 x 点，而是随机抽查一个点。

什么是 t(x)?

​其实前面已经提到过了
t(x) = (x-1)(x-2)…(x-d)，其中 d 是门电路的个数

Groth 大牛，在2016年提出了 Groth16 算法。该算法大大缩小了证明的数据量，并且也大大提高了验证证明的速度。从 PPT 中，我们可以看出验证过程只需要验证一个等式就可以了，所以验证特别快。
Groth16 中，证明依然需要提供三个值：A、B、C。但其实 Groth 已经从数学上证明了，最少可以只要两个值就可以作为证明。但由于计算量巨大，所以相比而言，三个值比较有实用价值。
具体的证明过程，这里就不展开了，具体可以阅读 “星想法”的公众号文章：《零知识证明 - Groth16算法介绍》

Groth16 算法中涉及到了很多密码学的知识，包括：椭圆曲线、同态隐藏、双线性映射等。
最后，为什么零知识证明可以做到零交互（Non-interactive）呢？
其实原理就是利用 CRS（Common Reference String）。CRS 其实就把挑战过程中所要生成的随机数和挑战数，都预先生成好，然后基于这些随机数和挑战数生成他们对应的在证明和验证过程中所需用到的各种同态隐藏。
之后，就把这些随机数和挑战数销毁。这些随机数和挑战数 被称为 toxic waste。之所以把他们称为 toxic waste，是因为如果他们没有被销毁的话，就可以伪造证明了。

在 Zcash 项目中，大家为了安全的生成这些随机数和挑战数，使用了 MPC 技术。这样多方一起来生成 这些 toxic waste，只要不是所有人合谋，那么没有人能恢复出 toxic waste。从而保证了安全性。
看完这一期的分享，你是否对 ”零知识证明–zkSNARK” 有了全面的了解呢？如果您意犹未尽，想要了解更多的零知识证明的相关知识，可以阅读李星老师公众号 “星想法” ，有更多的延展内容可以学习。

同时我们将在8月31日（周六）举办第三期 PPIO Code Talks 活动，此次活动我们更是邀请到了神秘重量级嘉宾，来分享关于区块链中密码学应用和联盟链技术与商业落地的相关问题。

如果您也是区块链从业者，对区块链技术有自己独特的心得，或者你有区块链相关技术干货希望与志同道合的技术爱好者分享，欢迎报名参加我们第三期 PPIO Code Talks！

后台回复“报名表”即可收到报名链接。为了保证 Code Talks 社区及技术沙龙的质量，提高参加者的参与体验，我们将对报名者进行项目背景信息和行业技术实力两方面的甄选。对核心技术开发人员，区块链从业者我们会发出最诚挚的邀请，并会有专人联系告知后续的参会细则。我们在 Code Talks 等待实力满分的你，一起共建区块链技术社区，碰撞出技术讨论的火花！
下一期文章，我们将会继续报道技术大咖王伯洋老师的分享《数字货币交易所架构初探》，关注 PPIO 公众号，精彩正在上演。

想了解更多有关 PPIO 的信息，可以移步官网：pp.io