深度学习《Deep Learning》读书笔记 - 第二章线性代数

线性代数其实在大一的时候学习过，但过了四年忘的差不多了，所以再次系统学习一下
在这里附上一篇能比较好说明矩阵意义的文章 ->链接

2.1 标量、向量、矩阵和张量

标量：单独的数
向量：一列数,可以把向量看作空间中的点，每个元素是不同坐标轴上的坐标
$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$
矩阵：二位数组，每一个元素由两个索引决定。
$$\left[\begin{array}{cc}{A}_{1,1}& A_{1,2}\\ A_{2,1}& A_{2,2}\end{array}\right]$$
张量： 超过二维的数组
转置：$(A^T{)}_{i.j}=A_{j,i}$，标量的转置等于它本身


矩阵的形状一样时，矩阵是可以相加的。
矩阵和向量相加：$C_{i,j}=A_{i.j}+b_j$，意思就是向量b和矩阵A的每一行相加.

2.2 矩阵和向量相乘

矩阵乘积：矩阵A的列数要和矩阵B的行数相等。
$$A^{m\times n}{B}^{n\times p}=C^{m\times p}$$
乘法操作(标准乘积)：
$$C_{i,j}=\sum _k{A}_{i,k}{B}_{k,i}$$
两个相同维数的向量x和y的点积可以看作矩阵$x^{T}y$：
$$x=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$
$$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]$$
$$x\cdot y=\left[\begin{array}{c}{x}_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n\end{array}\right]$$
矩阵乘积运算服从分配律，结合律，不满足交换律。两个向量的点积满足交换律。
矩阵乘积的转置：
$$(AB{)}^T=B^T{A}^T$$

2.3 单位矩阵和逆矩阵

单位矩阵： 所有沿主对角线的元素都是1，其他为0
$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
单位矩阵极为$I_n$，$I_n\in R^{n\times n}$
$$\forall x\in R^n,I_{n}x=x$$
$A$的逆矩阵计为$A^{-1}$：$A^{-1}A=I_n$

2.4 线性相关和生成子空间

一组向量的线性组合，是指每个向量乘以对应标量系数之后的和：
$$\sum _i=c_i{v}^{(i)}$$
一组向量的生成子空间，是原始向量线性组合后所能抵达的点的集合。

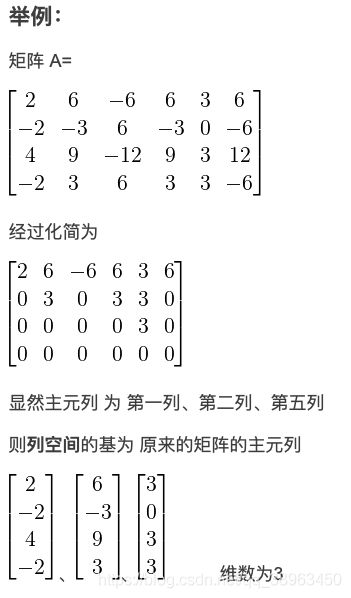
矩阵的列空间 ColA(参考链接)
对于 m×n 矩阵$A$，列空间就是$A$的各列的线性组合的集合，记为 ColA，是$R^m$的一个子空间，由 矩阵的主元列构成，即Ax=b中，方程的解基本变量。

确定$Ax=b$是否有解，相当于确定向量$b$是否在A列向量的生成子空间中。这个特殊的生成子空间被称为$A$的列空间或者$A$的值域


线性无关：一组向量中的任意一个向量都不能表示成其他向量的线性组合
线性相关：某个向量是一组向量中某些向量的线性组合，将这个向量加入这组向量后不会增加这组向量的生成子空间
如果一个矩阵的列空间涵盖整个$R^m$，说明该向量集恰好有m个线性无关的列向量。

2.5 范数

范数：衡量一个向量的大小。形式上，$L^p$范数定义如下：
$$\parallel x{\parallel }_p=(\sum _i|x_i{|}^p{)}^{\frac{1}{p}}$$
其中$p\in R$，$p\ge 1$。
范数是将向量映射到非负值的函数。直观上来说，向量$x$的范数衡量从原点到点$x$的距离。
当$p=2$时，$L^2$范数称为欧几里得范数，它表示从原点出发到向量$x$的点的欧几里得距离。经常简化表示为$\parallel x\parallel$。


$L^1$范数可以简化为：
$$\parallel x{\parallel }_1=\sum _i|x_i|$$
另一个在机器学习中经常出现的是$L^{\infty }$，也被称为最大范数，最大范数表示向量中具有最大幅值的元素的绝对值：
$$\parallel x{\parallel }_{\infty }=ma{x}_i|x_i|$$
Frobenius范数：衡量矩阵的大小
$$\parallel A{\parallel }_F=\sqrt{\sum _{i,j}{A}_{i,j}^2}$$

2.6 特殊类型的矩阵和向量

对角矩阵：只在主对角线上含有非零元素，其他位置都是零。
用diag(v)表示对角元素由向量$v$中元素给定的一个对角方阵。
计算乘法diag$(v)x$，只需要将$x$中的每个元素$x_i$放大$v_i$倍，diag$(v)x=v\odot x$
对角方阵的逆矩阵：diag$(v{)}^{-1}=$diag$([1/v_1,\cdots ,1/v_n]{)}^T$

对称：矩阵的转置和自己相等，$A=A^T$
单位向量：具有单位范数的向量，$\parallel x{\parallel }_2=1$
正交：如果$x^{T}y=0$，那么向量$x$和$y$互相正交。如果两个向量都有非零范数，那么这两个向量之间的夹角是90度。如果这些向量不仅互相正交，同时范数都为1，那称为标准正交。
正交矩阵：$A^{T}A=A{A}^T=I$，这意味着$A^{-1}=A^T$

2.7 特征分解

特征分解：将矩阵分解成一组特征向量和特征值
方阵$A$的特征向量$v$：
$$Av=\lambda v$$
其中标量$\lambda$称为这个特征向量对应的特征值。

>参考链接
一个矩阵的一组特征向量是一组正交向量。特征分解是将一个矩阵分解成下面的形式：
$$A=Vdiag(\lambda )V^{-1}$$
其中$V$是这个矩阵$A$的特征向量组成的矩阵，$diag(\lambda )$是一个对角阵，每一个对角线上的元素就是一个特征值。

所有特征值都是正数的矩阵称为正定，所有特征值都是非负数的矩阵称为半正定；所有特征值都是负数的矩阵称为负定，所有特征值都是非正数的矩阵称为半负定。

2.8 奇异值分解

奇异值分解：将矩阵分解为奇异向量和奇异值
每个实数矩阵都有一个奇异值分解，但不一定有特征分解。非方阵的矩阵没有特征分解。
将矩阵$A$奇异值分解：
$$A=UD{V}^{-1}$$
$A$是一个$m\times n$的矩阵，$U$是一个$m\times m$的矩阵,$D$是一个$m\times n$的矩阵，$V$是一个$n\times n$的矩阵，$U$和$V$都是正交矩阵，$D$是对角矩阵。对角矩阵$D$对角线上的元素是奇异值。

2.10 迹运算

迹运算返回的是矩阵对角元素的和：
$$Tr(a)=\sum _i{A}_{i,i}$$
迹运算提供了另一种描述矩阵Frobenius范数的方式：
$$\parallel A{\parallel }_F=\sqrt{Tr(A{A}^T)}$$

2.11 行列式

行列式记为det(A)，等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。