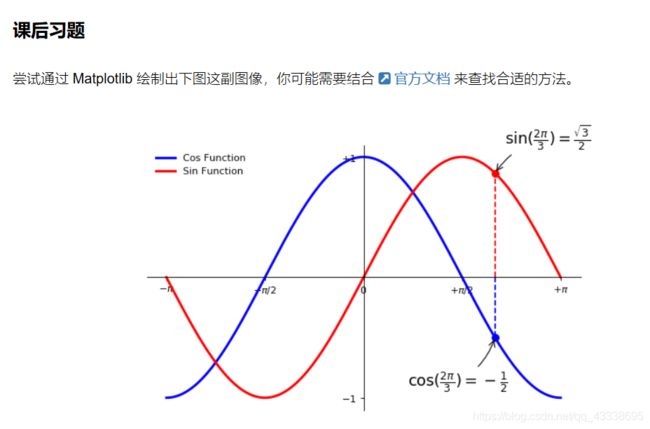
【实验楼/matplotlib.pyplot】绘制笛卡尔坐标系+注释+图例

博主的github链接，欢迎大家来访问~：https://github.com/Sh-Zh-7

强化学习经典算法实现地址：https://github.com/Sh-Zh-7/reinforce-learning-impl

一. 问题描述

二. 问题分析

做这种问题我们应该先把图的大致模样画出来，然后再去考虑细节。

这里一个比较难的点是笛卡尔直角坐标系的绘制，因为我们默认的图都是使用矩形状的坐标系的。

稍微总结一下，大概可以分这么几步走：

1.  绘制直角坐标系
2.  绘制两个三角函数
3.  绘制两条直线
4.  绘制annotation
5. 绘制图例

下面，我就一步一步来实现它。

 

三. 绘制直角坐标系

这里我介绍两种方法。

第一种在矩形图上直接修改的。主要是把右边和上面的两条矩形边界给抹除了。

# 在这里我不得不吐槽matplotlib的官方文档做的实在是太不好了
# 很多api都只有声明和源码，没有具体的解释
# 想要找到具体的用法只能是在网上找博客
import numpy as np
import matplotlib.pyplot as plt

# 创建画板和画布对象
plt.figure(figsize=(8, 5), dpi=80)
ax = plt.subplot(111)

# 这次不整个消失了
# 我们选择将右边及上面的矩形边框删除掉
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

# 设置坐标轴上数据的方向
# 0是和我们普通笛卡尔坐标系相一致的，1则是相反的
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

第二种就是使用mpl_axisartist。这个模块专门是用来绘制坐标轴的。

其功能十分强大，还可以给我们的坐标轴添加上正方向的箭头。添加一些注释啊什么的。

import numpy as np #导入数值计算模块
import matplotlib.pyplot as plt #导入绘图模块
import mpl_toolkits.axisartist as axisartist #导入坐标轴加工模块

fig=plt.figure() #新建画布
ax=axisartist.Subplot(fig,111) #使用axisartist.Subplot方法创建一个绘图区对象ax
fig.add_axes(ax) #将绘图区对象添加到画布中

ax.axis[:].set_visible(False) #隐藏原来的实线矩形

ax.axis["x"]=ax.new_floating_axis(0,0,axis_direction="bottom") #添加x轴
ax.axis["y"]=ax.new_floating_axis(1,0,axis_direction="bottom") #添加y轴

ax.axis["x"].set_axisline_style("->",size=1.0) #给x坐标轴加箭头
ax.axis["y"].set_axisline_style("->",size=1.0) #给y坐标轴加箭头
ax.annotate(s='x' ,xy=(2*math.pi,0) ,xytext=(2*math.pi,0.1)) #标注x轴
ax.annotate(s='y' ,xy=(0,1.0) ,xytext=(-0.5,1.0)) #标注y轴

（P.S. 如果是使用pyplot中的subplots方法，是不会成功的；所以老老实实使用axisartist方法把！）

 

四. 绘制我们的函数图像

很显然我们得使用我们的plot函数，这里顺便提一下我们plot函数的三种用法

1.  给定X和Y的所有点，绘制矢量曲线图。
2. 直接给定一个X和关于X的函数（e.g. X + 1）， 根据表达式的内容来绘制。
3. 传入两个list，每一个list中有两个元素，分别是x或者y的起始和终末位置；按照这两个坐标来绘制直线。

绘制sin和cos的话我们使用第一个方法，绘制后面的linestyle为"--"的直线我们使用第三个方法。

我们可以使用Python的sequence unpacking来简单赋值。

# 准备数据，利用sequence unpacking
X  = np.linspace(-np.pi, np.pi, 100, endpoint=True) # 这个endpoint非常细节
C, S = np.cos(X), np.sin(X)

# 绘制图像
plt.plot(X, C, color='b', label="Cos Function")
plt.plot(X, S, color='r', label="Sin Function")

# 绘制linestyle="--"的两条直线
t = np.pi * 2 / 3;
plt.plot([t, t], [0, np.sin(t)], color='r', linestyle="--")
plt.plot([t, t], [0, np.cos(t)], color='b', linestyle="--")

 

五. 修改坐标系上的刻度

这里我们要做两件事：

1.  确定整条坐标轴所能表示的范围。——plt.xlim, plt.ylim
2.  确定坐标轴上哪些数字要被特别表示，然后还要标出来。——plt.xticks, plt.yticks

# 修改图中坐标系表示的最大和最小值
plt.xlim(X.min() * 1.1, X.max() * 1.1)
plt.ylim(-1.1, 1.1)

# 修改坐标轴上的标签
x_numbers = [-np.pi, -np.pi / 2, 0, np.pi / 2, np.pi]
x_labels = [r"$-\pi$", r"$-\pi$", r"$0$", r"$\pi/2$", r"$\pi$"] # python中使用LaTex得加上$$, 最好向他这样转义
plt.xticks(x_numbers, x_labels)
y_numbers = [-1, 1]
y_labels = ["-1", "1"]
plt.yticks(y_numbers, y_labels)

 

六.  绘制注释

绘制那两个散点我们就不提了，这里直接讲怎么绘制注释：

从matplotlib中我们发现：

1. xy是你在图中要注释的点。
2. xytext是注释的位置。
3. xycoords和textcoords似乎是各种偏移量？反正这个用默认值就好
4. arrorprops是箭头。

# 补充记号
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
             xy=(t, np.sin(t)), xycoords='data',
             xytext=(+10, +30), textcoords='offset points', fontsize=16,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
             xy=(t, np.cos(t)), xycoords='data',
             xytext=(-90, -50), textcoords='offset points', fontsize=16,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

 

七. 绘制图例

图例的绘制也是一个plot.legend了事，不过这里我不会这么讲。

我想提的是：如果你在之前plot中给定了label的时候，这里就不需要显示给定label，

只要传入关键字参数，把我们的边框消除掉即可。

# 设置图例
# 如果上面制定了label, 那这里就不用传入列表！
plt.legend(frameon=False)

 

八. 源码

https://labfile.oss.aliyuncs.com/courses/892/sin_cos_functions.py