并查集原理及Python实现，朋友圈个数问题

背景问题：给定一些好友的关系，求这些好友关系中，存在多少个朋友圈？

例如给定好友关系为：[0,1], [0, 4], [1, 2], [1, 3], [5, 6], [6, 7], [7, 5], [8, 9]。在这些朋友关系中，存在3个朋友圈，分别是

【0,1,2,3,4】，【5,6,7】，【8,9】

如下图所示：

这个问题，抽象一下，就是：求一个图的连通子图的个数，即连通度是多少。

第一种方法，采用DFS遍历这个图，遍历过程中，可以求出连通度，但是DFS对于大型图，效率缓慢。

第二种方法，采用并查集。并查集可以说是一种算法，或者数据结构。

 

并查集的主要思想是，对每一个连通的子图，选出一个节点，作为代表。“代表”的个数，就是连通度的大小。

步骤如下：

1. 初始化每个节点的代表为其本身（后面，把代表叫做“父节点”）。

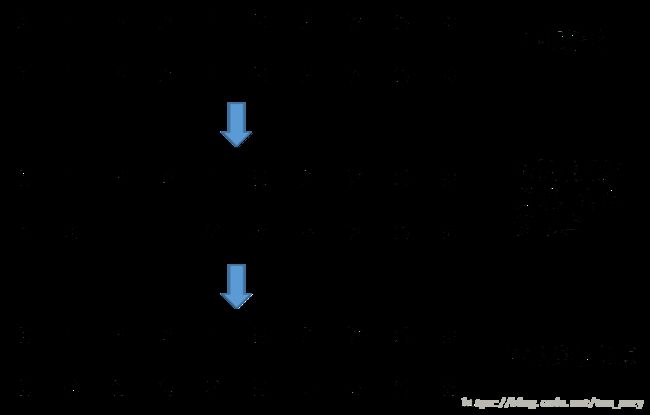
2.针对给定的好友关系[0,1], [0, 4], [1, 2], [1, 3], [5, 6], [6, 7], [7, 5], [8, 9]，更新父节点。例如给出(1,2)那么，更新2的父节点为1。

3.重新更新所有节点的父节点，针对每个节点，找到其祖宗节点，即根节点。

对应的步骤如下：上面的是节点本身，下面的是节点对应的父节点或根节点。

这样，就将节点分成了3类，每个类用一个节点作为代表。

Python代码如下：

def union_find(nodes, edges):
    father = [0]*len(nodes)     # 记录父节点
    for node in nodes:  # 初始化为本身
        father[node] = node

    for edge in edges:  # 标记父节点
        head = edge[0]
        tail = edge[1]
        father[tail] = head

    for node in nodes:
        while True:         # 循环，直到找到根节点
            father_of_node = father[node]
            if father_of_node != father[father_of_node]:
                father[node] = father[father_of_node]
            else:           # 如果该节点的父节点与其爷爷节点相同，
                break       # 则说明找到了根节点

    L = {}
    for i, f in enumerate(father):
        L[f] = []
    for i, f in enumerate(father):
        L[f].append(i)

    return L


if __name__ == '__main__':
    nodes = list(range(0, 10))
    test_edges = [[0, 1], [0, 4], [1, 2], [1, 3], [5, 6], [6, 7], [7, 5], [8, 9]]

    L = union_find(nodes, test_edges)
    print(L)
    print('num of pyq:', len(L))

运行结果如下：

 

参考

1.【图解算法】并查集 —— 联合查找算法

2.并查集解决朋友圈问题

 

————————————————————————更新——————————————————————————————

上面代码有误，（可能）正确代码如下：

def union_find(edges):
    nodes = []
    for edge in edges:
        if edge[0] not in nodes:
            nodes.append(edge[0])
        if edge[1] not in nodes:
            nodes.append(edge[1])

    node_father = {}
    for node in nodes:
        node_father[node] = node

    for edge in edges:
        if node_father[edge[1]] == edge[1]:
            node_father[edge[1]] = edge[0]
        else:
            node_father[edge[0]] = edge[1]

    print(node_father)

    for node in nodes:
        father = node_father[node]
        print(node)
        while father != node_father[father]:
            father = node_father[father]
        node_father[node] = father
    return len([node_father.keys()]), node_father


if __name__ == '__main__':
    nodes = list(range(0, 10))
    test_edges = [['F', 'H'], ['A', 'C'], ['H', 'A']]
    test_edges2 = [[1,2], [3, 2], [4, 2]]
    n, pyq = union_find(test_edges)
    print(n,' ', pyq)