几种简单的图像加密方法
图像加密的重要性可想而知,每个人都会有自己的小秘密,通过图像加密的方法可以保护自己的照片等的安全。
一般情况下,图像加密可以分为以下几个步骤:
1.选择图像加密算法
2.根据算法获取秘钥
3.根据保存的秘钥解密
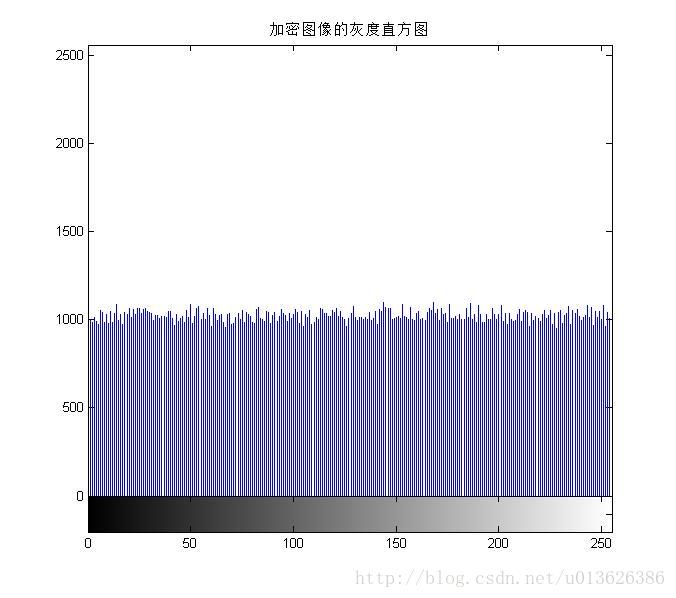
图像加密的处理方式多为对图像中的像素点进行处理,有的处理方式不改变灰度直方图的信息(易破解),然后更高级的处理方式使得原来的灰度直方图信息也发生改变(比如变得均衡化了)。
下面介绍自己亲自测试的2种图像加密算法:
1.行列像素点置乱方法,该方法将原图中的像素信息进行了重新排布——置乱。通过一一对应的关系可以恢复原来的图像,此时的秘钥即为行列变换的映射向量Mchange和Nchange。
简单的MATLAB程序如下:
clc,clear all,close all
Lena = imread('Lena512.bmp');
figure;imshow(Lena)
title('原图')
[M,N] = size(Lena);
Rm = randsample(M,M)';
Mchange = [1:1:M;Rm];
Rn = randsample(N,N)';
Nchange = [1:1:N;Rn];
%打乱行顺序
Lena (Mchange(1,:),:) = Lena (Mchange(2,:),:);
figure;imshow(Lena)
title('行加密后图像')
%打乱列顺序
Lena (:,Nchange(1,:)) = Lena (:,Nchange(2,:));
figure;imshow(Lena)
title('列加密后图像')
%列变换还原
Lena (:,Nchange(2,:)) = Lena (:,Nchange(1,:));
figure;imshow(Lena)
title('列解密后图像')
%行变换还原
Lena (Mchange(2,:),:) = Lena (Mchange(1,:),:);
figure;imshow(Lena)
title('解密后图像')
2.基于混沌的图像加密方法,产生2个Logistic混沌序列,改造2个Logistic,得到两个y序列,由yl和y2序列对原图像进行值替代加密。秘钥为混沌系统的初始状态值。
可参考的MATLAB程序如下:
%加密方法,混沌序列
clc,clear all,close all
A=imread('Lena512.bmp');
imshow(A); title('原图')
[M,N]=size(A);%原始图像A的尺寸一MxN
u1=4;u2=4;x1(1)=0.2;x2(1)=0.7;
sumA=sum(sum(A));
k=mod(sumA,256)*1.0/255;
x1(1)=(x1(1)+k)/2; x2(1)=(x2(1)+k)/2;
y1(1)=(1/3.1415926)*asin(sqrt(x1(1)));
y2(1)=(1/3.1415926)*asin(sqrt(x2(1)));
for i=1:1:M*N-1 %产生2个Logistic混沌序列
x1(i+1)=u1*x1(i)*(1-x1(i));
x2(i+1)=u2*x2(i)*(1-x2(i));
end
for i=1:1:M*N %改造2个Logistic,得到两个y序列
y1(i)=(1/3.1415926)*asin(sqrt(x1(i)));
y2(i)=(1/3.1415926)*asin(sqrt(x2(i)));
end
n=1;
for i=1:1:M %由yl和y2序列对原图像进行值替代加密
for j=1:1:N
if mod(n,1)==0
k(n)=mod(floor(y1(n)*10^15),256);
else
k(n)=mod(floor(y2(n)*10^15),256);
end
A1(i,j)=bitxor(A(i,j),k(n)); %得到加密像素
n=n+1;
end
end
figure,imshow(A1);title('混沌加密图像') %输出得到的加密图像
n=1;
for i=1:1:M
for j=1:1:N
if mod(n,1)==0
k(n)=mod(floor(y1(n)*10^15),256);
else
k(n)=mod(floor(y2(n)*10^15),256);
end
A2(i,j)=bitxor(A1(i,j),k(n)); %得到加密像素
n=n+1;
end
end
figure,imshow(A2);title('解密图像') %输出得到的解密图像