信号与系统

献给

        期末预习的我
          还有刺猬

DAY1

    信号可以描述范围极为广泛的一类物理现象, 虽然信号可以用许多方式来表示, 但是在所有的情况下, 信号所包含的信息总是寄寓在某种变化形式的波形之中。
                            ----
    在数学上, 信号可以表示为一个或多个变量的函数. 信号与系统的学习将会伴随着有趣的数学学习~~~(真的有趣吗-v-)

信号的分类

    1. 确定信号与随机信号(按照信号的确定性来划分)
        确定信号: 能够以确定的时间函数表示的信号
        随机信号: 无法以确定的时间函数来描述
        信号一定是包含某种信息的数据流, 如果是"随机"那便需要随机的解析, 随机解析出来的信息也是随机的. 所以我认为信号都是确定的没有随机之说. 书上的随机是指: 无法以确定的时间函数来描述(用统计的规律来描述). 本渣觉得不妥, 因为无知....
    2. 连续时间信号和离散时间信号
        连续时间信号: 自变量是连续可变的
        离散时间信号: 自变量在离散的时刻点上有定义
        它们之间有个很重要的联系: 离散时间信号是通过对连续时间信号的采样而得到的. 可以理解为离散时间信号的极限是连续时间信号吧.
        进一步有:
            自变量和因变量都连续的信号: 模拟信号
            自变量和因变量都离散的信号: 数字信号
            (世界是数字的or世界史模拟的, 都错了, 世界是数学的)
    3. 周期信号与非周期信号(按照信号周期性划分)
        如果一个信号是周期信号: 1.  定义域为(-∞, +∞)   
                            2.  每隔一个固定的时间间隔重复变化
        数学语言描述: f(t) = f(t + T0),  -∞ < t < +∞
                    f[k] = f[k + N],   -∞ < N < +∞
        满足上式得最小正数T0, N称为周期信号的基本(基波)周期
    4. 信号能量与功率(借用一下书上的描述)
        在很多(但不是全部)应用中, 所考虑的信号是直接在与某个物理系统中具有能量和功率的一些物理量有关的. 例如若u(t), i(t)分别是阻值为R的某一段电阻上的电压和电流, 那么其瞬时功率为:
        p(t) = u(t) * i(t);
    在时间 t1 <= t <= t2, 内消耗的总能量就是
        E = ∫p(t)dt = ∫u(t)*u(t)/Rdt
    其平均功率为
        1/(t2 - t1)∫p(t)dt = 1/(t2 - t1)∫u(t)*u(t)/Rdt

    类似的, 可以对任何连续时间信号和离散时间信号采用类似功率和能量的术语(将信号看成具有复数值往往更为方便), 这时t1 <= t <= t2, 内的总能量对于一个连续时间信号x(t)来说就可以定义为:
        ∫|x(t)|*|x(t)|dt      (当然, 是定积分, 只是还不知道用公式编辑器)
        那么平均功率就是能量除以时间(t2- t1)
    离散时间信号也是类似的·····
    要牢记的是, 这里所用的"能量", "功率"与信号是否真正的关联了物理量无关!!!!(这样命名或许只是一次意外~~)
    并且, 在很多系统中关心的是信号在一个无穷区间内(-∞ < t < +∞)的功率和能量:
        E∞ = ∫|x(t)|*|x(t)|dt
    对于某些信号, 在无穷区间内的能量可能不收敛, 这样的信号具有无限的能量, 而E∞ < ∞ 的信号具有有限能量.
    利用这些定义就可以区分三种重要信号:
        1. 信号具有有限的总能量, 此时这种信号的平均功率为0;
        2. 信号具有有限的平均功率, 此时这种信号的总能量∞;
        3. 信号的总能量和平均功率都发散;

    至于信号能量和功率深刻的含义, 还需要继续学习~~

自变量的变换

信号与系统分析中一个重要的概念是关于信号的变换;
    自变量变换举例:
        1. 时移(time shift)
        2. 时间反转(time reversal)
        3. 时间尺度变换(time scaling)
        (其实就是, 平移, 旋转, 伸缩, 基本的函数变换)

    周期信号:
        x(t) = x(t + T0)

    偶信号与奇信号:
        1. 偶信号: x(t) = x(-t)
        2. 奇信号: x(t) = -x(-t)
        (其定义域必然对称, 奇信号过原点)
        一个有趣的事实, 任何信号都能分解为, 一个奇信号和偶信号之和:
            Ev{x(t)} = 1/2[x(t) + x(-t)] (偶部)
            Ov{x(t)} = 1/2[x(t) - x(-t)] (奇部)
            ---> 
            x(t) = Ev{x(t)} + Ov{x(t)}          

指数信号与正弦信号

    介绍几个基本的连续时间和离散时间信号, 这样做不仅仅是因为这些信号经常出现, 跟重要的是他们可以作为基本的信号构造单元来构成其他许多信号.

    连续时间复指数信号与正弦信号
        连续时间复指数信号具有如下形式:
                x(t) = Cexp(at);(C, a一般为复数, 那么复数的意义是什么呢)
                根据这些参数的不同, 复指数信号可有几种不同的特征
        1. 实指数信号
            C, a都是实数时, 这时的x(t)称为实指数信号;
            当a大于0时, 指数级增长(可以用来描述原子爆炸或复杂化学反应中链锁反应等很多不同的物理过程)
            当小于0时, 指数级衰减(可以用来描述放射性衰变, RC电路及由阻尼的机械系统响应等广泛的各种现象)

        2. 周期复指数信号和正弦信号
            a为纯虚数, 考虑如下信号:
                x(t) = exp(jΩt)
            伟大的欧拉关系: exp(jθ) = cos(θ) + jsin(θ)
                exp(jπ) = 1, 有趣~~ 
                ---> 2*cos(θ) = exp(jθ) + exp(-jθ)
                ---> 2*sin(θ) = exp(jθ) - exp(-jθ)
            [将指数函数泰勒展开能得到, 此处有待证明]
            可以知道x(t)的周期为2π/Ω, Ω称为基波频率
            所以复指数信号与正弦信号密切相关, 或与是同一事物的不同体现吧。
            正弦和周期复指数信号也可以用来描述很多物理过程的特性, 尤其是储存能量的系统(LC电路, 简谐运动~~~)
            周期信号, 给出了具有无限能量但有有限功率的的这类信号的例子. 通过计算一个周期内的能量和平均功率可以得出:
            E = ∫|exp(jΩt)|*|exp(jΩt)|dt
            |exp(jΩt)| = | cos(Ωt) + jsin(Ωt) | = 1
            虚指数的模总是为一 -o-
            ---> E = T0;
            ---> P = 1;
            进一步对于无穷周期: E = ∞;
                             P = 1;

            周期复指数信号在讨论信号与系统的大部分问题中都起着十分重要的作用, 部分原因是由于对于其它大多数信号来说, 它们可以用来作为极其有用的信号基本构成单元. 同时, 一组成谐波关系(harmonically related)的复指数信号也是很有用的; 也就是说, 周期复指数信号的集合内的全部信号都是周期的, 且有一个公共周期T0. 具体而言, 对于一个复指数信号exp(jΩt), 要使其成为具有周期为T0的周期信号的必要条件是:
            exp(jΩT0) = 1;
            即: ΩT0 = 2πk  (k = 0, +-1, +-2, ····)
            Ω = 2πk/T0 , Ω是Ω0 = 2π/T0的整数倍

            φk(t) = exp(jkΩt)
                    |k| == 1: 称为基波
                    |k| != 1: 称为k次谐波
        一个成谐波关系的复指数信号集合就是一组其基波频率是某一正频率Ω0的整数倍的周期复指数信号.
        (预示着接下来的傅里叶~~~)

    3. 一般指数信号
        最一般情况下的复指数信号可以借助于已经讨论过的实指数信号和周期复指数信号来表示和说明. 考虑某一复指数Cexp(at), 将C用极坐标, a用笛卡尔坐标表示, 分别有:
            C = |C|exp(jθ)
            a = r + jΩ
        那么:
            Cexp(at) = |C|exp(rt)exp(j(Ωt + θ))
                = |C|exp(rt)cos(Ωt + θ) + j|C|exp(rt)sin(Ωt + θ)
        如果r > 0 , 指数增长的正弦信号
           r < 0 , 指数衰减的正弦信号
        具有指数衰减振幅的正弦信号常称为 阻尼正弦振荡(例如: RLC电路和包括阻尼和恢复力的机械系统)

离散时间复指数信号与正弦信号

    将连续离散化即可, 分析方法相似~~
    但是·····
    离散时间复指数序列的周期性质却存在一些重要的差异

单位冲激与单位阶跃函数

    1. 离散时间单位脉冲与单位阶跃序列
        单位脉冲(单位样本)
            δ[n] = 0, n != 0;
            δ[n] = 1, n == 0;
        单位阶跃
            u[n] = 0, n < 0;
            u[n] = 1, n >= 0;
        这两者之间存在密切联系
            δ[n] = u[n] - u[n-1];              {一次差分}
            u[n] = Σδ[i] (i from -∞ to n);     {求和}

        x[n]δ[n-n0] = x[n0], 这就是为什么叫单位样本, 它可以采样呀~

    2. 连续时间单位阶跃和冲激函数

        单位阶跃函数:
            u(t) = 0, t < 0;
            u(t) = 1, t >= 0;
        单位冲激函数:
            δ(t) = "1", t = 0; {"1": 冲激强度}
            δ(t) = 0, t != 0;   

        类似的:
            u(t) =∫δ(τ)dτ (τ from -∞ to t)
            那么是不是有
                --->? δ(t) = du(t) / dt
                问题来了, u(t)并不连续所以是不可微的!!!
                从数学上来解释是困难的, 那么把单位阶跃函数近似一下, 因为现实中几乎不会存在突变, 那近似uΔ(t)是经过时间Δ从0变为1的:
                    δΔ(t)*dt = duΔ(t)
                    ∫δΔ(t)*dt  = uΔ(t), 当t > Δ时, 积分结果为1
                说明冲激函数围成的矩形面积为1
                当 limΔ->0时, 便得到冲激函数的值, 此时这个值趋于无穷, 用强度"1"表示.
            x(t)δ(t-t0) = x(t0), 它也可以进行采样哦
            单位冲激函数应该看成一种理想化的东西, 任何物理系统都会有惯性存在, 因此不可能对输入做出瞬时的响应!

连续时间系统和离散时间系统

    连续时间系统: 输入该系统的信号是连续时间信号, 系统产生的输出也是连续时间信号
        x(t) --> y(t)
    离散事件系统: 输入该系统的信号是离散时间信号, 系统产生的输出也是离散时间信号
        x[n] --> y[n]

    简单系统举例
        建立分析和设计系统的一般方法的重要根据之一就是:很多不同应用场合的系统都具有非常类似的数学描述形式···

        example 1: RC电路

        i(t) = {Us(t) - Uc(t)} /  R;
        i(t) = C * dUc(t) / dt;
        ----> dUc(t)/dt + Uc(t)/RC = Us(t)/RC;

        example 2: 

        m*dV(t)/dt = F(t) - kV(t);
        dV(t)/dt + kV(t)/m = F(t)/m;

        这两个物理过程不同, 但输入输出关系的方程却基本是一样的(一阶线性微分方程)

        example 3: 离散事件系统的一个例子
        考虑某一银行户头按月结余的一个简单模型: 令y[n]为n月末的结余, 假设y[n]按月依下列方程变化:
        y[n] = 1.01*y[n-1] + x[n];
        或 y[n] - 1.01*y[n-1] = x[n];(x[n]为n个月的净存款)

        example 4: 考虑example 2中简单的一种数字仿真
        将时间分解为长度为Δ的离散间隔, 并用一阶向后差分来近似微分
            (V(nΔ) - V((n-1)Δ))/Δ ----> dV(nΔ)/dt
            则原式 : V[n] - (m/(m+kΔ))V[n-1] = (Δ/(m+kΔ))f[n]
        咦···这不就是一阶线性差分方程了, 连续和离散紧密相关~~~

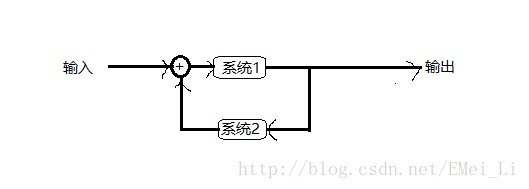
系统的互连

    串联(级联): 

    并联:

    反馈互连:

基本系统性质

    1. 记忆系统与无记忆系统
            如果对自变量的每一个值, 一个系统的输出仅仅取决于该时刻的输入这个系统称为 无记忆(memoryless)系统
            在很多系统中记忆是直接与能量存储相联系的~~
            记忆系统的概念, 一般总是让人想到储存过去的输入和输出值, 但是我们所给出的定义也会导致把当前的输入和输出与输入输出的将来值有关的系统也称为记忆系统!BOOK 11

    2. 可逆性与可逆系统
            一个系统如果在不同的输入下, 导致不同的输出, 就称该系统是可逆的.
            如果一个系统是可逆的, 那么一定有一个逆系统存在, 当该系统与逆系统级联后就会产生一个输出w[n]等于第一个系统的输入x[n].

    3. 因果性
            如果一个系统在任何时刻的输出只取决于现在的输入以及过去的输入, 该系统就成为因果系统.

    4. 稳定性
            一个稳定系统, 若其输入是有界的, 则系统的输出也必须是有界的.

    5. 时不变性
            系统的特征和行为不随时间而改变.

    6. 线性
            1. 可加性
            2. 齐次性