Matlab Robotics Toolbox--坐标系变换

Matlab Robotics Toolbox–坐标系变换

摘要

坐标变换一般可由旋转变换和平移变换两部分构成，上一篇介绍了Robotics Toolbox旋转变换的相关函数，这一篇介绍坐标系齐次变换的函数。

平移变换

（1）创建平移变换矩阵

• T=transl(x,y,z) : 表示能够获取一个分别沿着x,y,z轴平移一段距离得到的4x4齐次变换矩阵。
• T=transl§ : 表示由经过矩阵（或向量）p=[x,y,z]的平移得到的其次变换矩阵。如果p为（Mx3）的矩阵，则T为一组其次变换矩阵（4x4xM）,其中T（：，：，i）对应于p的第i行。

例如

>> T=transl(1,2,3)

T =

     1     0     0     1
     0     1     0     2
     0     0     1     3
     0     0     0     1
     
>>p=[2 3 4];
>>T=transl(p)

T =

     1     0     0     2
     0     1     0     3
     0     0     1     4
     0     0     0     1

（2）使用transl()获取一个矩阵中的平移分量。

• [x ,y, z]=transl(T): x,y,z是齐次变换矩阵T中的三个分量，是一个1xM的向量。
• p=transl(T): p是齐次变换矩阵T中平移部分，是一个3xM的矩阵。

例子

T=transl(3,4,5)

T =

     1     0     0     3
     0     1     0     4
     0     0     1     5
     0     0     0     1

>> p=transl(T)

p =

     3
     4
     5

>> [x,y,z]=transl(T)

x =

     3


y =

     4


z =

     5

旋转坐标变换

• T=trotx($\theta$): 表示绕X轴旋转$\theta$得到的齐次变换矩阵（4x4);
• T=troty($\theta$): 表示绕Y轴旋转$\theta$得到的齐次变换矩阵（4x4);
• T=trotz($\theta$): 表示绕Z轴旋转$\theta$得到的齐次变换矩阵（4x4);

矩阵分解

• R=t2r(T):获取齐次变换矩阵T中正交旋转矩阵分量。如果T是一个4x4的旋转矩阵，则R是一个3x3的矩阵，如果R是一个3x3的矩阵，则R是一个2x2的矩阵。

例子

>> T=trotx(30)*transl(3,4,5)

T =

    1.0000         0         0    3.0000
         0    0.8660   -0.5000    0.9641
         0    0.5000    0.8660    6.3301
         0         0         0    1.0000

>> R=t2r(T)

R =

    1.0000         0         0
         0    0.8660   -0.5000
         0    0.5000    0.8660

• T=r2t®可将旋转矩转换为齐次矩阵，获取一个正交旋转矩阵R等价的具有零平移分量的其次变换矩阵。如果R是一个3x3的矩阵，则T是一个4x4的矩阵；如果R是一个2x2的矩阵，则T是一个3x3的矩阵。

例子

>> R=rotz(60)

R =

    0.5000   -0.8660         0
    0.8660    0.5000         0
         0         0    1.0000

>> T=r2t(R)

T =

    0.5000   -0.8660         0         0
    0.8660    0.5000         0         0
         0         0    1.0000         0
         0         0         0    1.0000

例子：坐标系{A}与坐标系{B}重合，首先{B}相对于{A}的$y_A$轴旋转60度，再沿{A}的x轴移动4个单位，最后沿着A的z轴移动3个单位。求点$p_1$在坐标系B中描述为${}^B{p}_1=[2,4,3{]}^T$，求它在坐标系A中的描述。

用toolbox仿真如下

clc
clear
close('all')
%%坐标系正变换，坐标点逆变换
T1=troty(60);
T2=transl(4,0,3);
T=T2*T1;
p1=[2;4;3;1];
Ap1=T*p1;
%%坐标系逆变换，坐标点正变换
Tr=inv(T);
Bp1=Tr*p1;
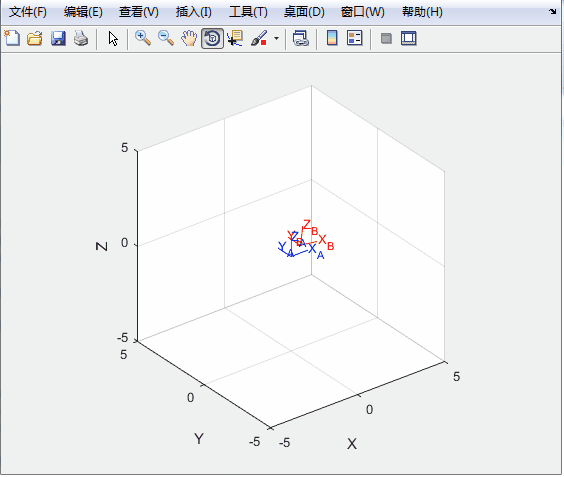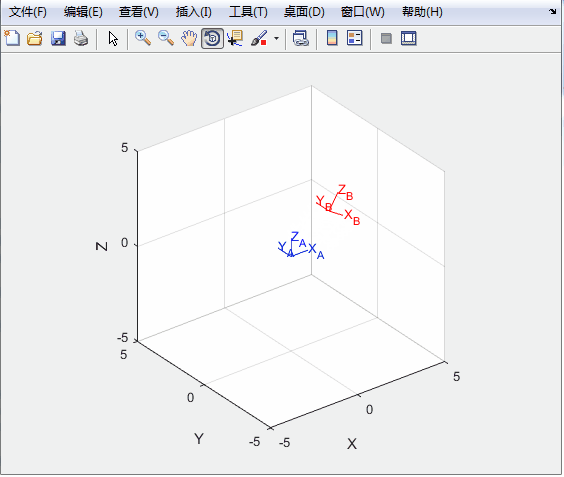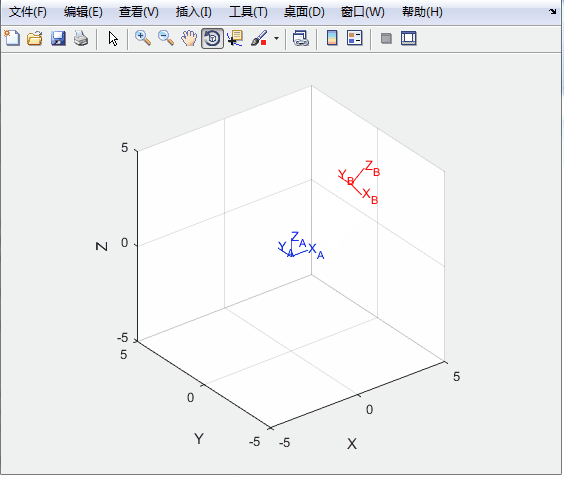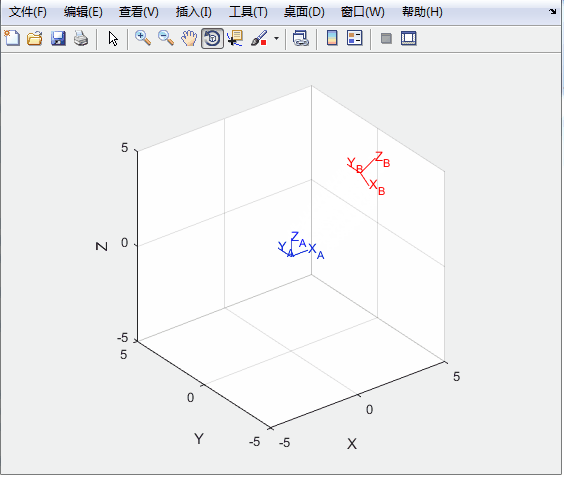
%%绘图
T0=transl(0,0,0);
trplot(T0,'frame','A','color','b');
axis([-5 5 -5 5 -5 5]);
hold on,
tranimate(T0,T,'frame','B','color','r');

参考文献

[1]机器人仿真与编程技术[M].杨辰光，李智军，许杨.北京：清华大学出版社，2018