DeepLab系列
- DeepLab V1: AFully Connected CRFs
- Dilated Conv & Receptive Field
- CRFs for accurate localization
- Deeplab V2: astrous spatial pyramid pooling
DeepLab是Google团队一系列semantic image segmentation的paper,截止2018年,共4篇,奉为经典,下面是笔记。
DeepLab V1: AFully Connected CRFs
ICLR 2015.
Abstract: 当前的图像分割CNN是根据classification这种high-level semantics改编的,但CNN有invariance特点,故会丢失localization信息,即无法对像素点精确定位语义(low-level semantics)。而本文提出的model,是CNN和PGM(概率图模型)的结合,对CNN最后一层加上fully connected CRFs,使得分割更精确。
取得的accuracy不详述了,另外通过network re-purposing和hole algorithm,使得处理时间很快。
这不禁让我产生疑问:
- high-level和low-level semantics区别在哪里?CNN的invariance是什么?平移不变性?那和high-level,hierarchical abstractions of the data什么关系?
解答:
- 所谓high low的界定是模糊的,大体上low-level是local,人肉眼能识别的最小单位,如十几个像素点构成的line,edge等,而很多个low-level features组成了high-level feature,给人以global info。故整个vision recognition是个hierarchical model,从识别许多个low-level,一层又一层,往上提高level,然后组成high-level。而CNN实现了这个流程,有很棒的high-level vision,但牺牲了low-level(因为Localization),故分割需要改进。https://www.zhihu.com/question/264702008
- 我突然理解了不变性对图像分割的制约。因为不变性是指图像的语义信息无论怎么平移,最终识别的分类是一样的,而这丢失了位置信息。
- 另外,卷积本身具有平移不变性,只不过是激活了不同区域的feature map,交换最终的fc层的元素,但不影响判断。pooling层也有不变性。(此处略)https://www.quora.com/How-is-a-convolutional-neural-network-able-to-learn-invariant-features
Introduction的结尾作者提到了模型的三大优点:speed, accuracy, simplicity.
Dilated Conv & Receptive Field
第一个是图像尺寸大小公式,由等差数列项数公式即得。
关键是第三个公式:r表示receptive field。我们直接在原始图像上考虑,上一层的感受野(即在原始图像上)为 rin r i n ,其在原始图像上的stride为 jin=Πi<insi j i n = Π i < i n s i ,故由等差数列求和公式即得。
感受野的通项公式为: rn=1+∑i≤n(ki−1)Πj<isj r n = 1 + ∑ i ≤ n ( k i − 1 ) Π j < i s j
也就是说,感受野和每层的kernel size和stride成正相关,且浅层的stride与深层的kernel size起到至关重要的作用。
http://blog.csdn.net/bojackhosreman/article/details/70162018?locationNum=11&fps=1
逻辑:为了减少localization info的丢失,我们需要扩大feature map size(即减少下采样),也减少stride,但这样会造成receptive field的减少,对semantic info不利。故使用hole algorithm即dilated convolution,实现Both large feature map & receptive field.
原理见图:图源 http://blog.csdn.net/c_row/article/details/52161394


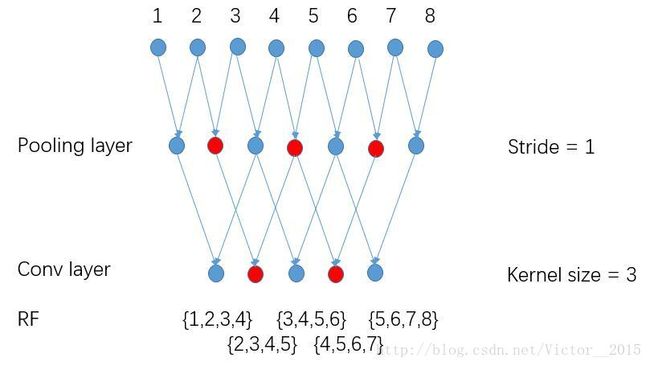
以后我们画神经元,可以考虑看线而非面,并且通过这样连接两层的方式,简洁明了。stride=1时,相邻的神经元其感受野重合度很高,如果卷积核连续的遍历,就有了冗余。相比之下,空洞卷积,每隔几个选一个参与卷积运算,保证了各个感受野交集的最小化。
但是感受野不能太大,太大丢失了位置信息,文章通过减少fc层参数4倍,控制感受野。**
总之,感受野要在一个合理的区间,在语义与位置信息中谋求平衡,并辅之以dilated conv,扩大感受野、保持大的feature map的同时减少参数。
CRFs for accurate localization
FCN-based model因为经过层层下采样和上采样(参数多,感受野大且重合),而丢失大量位置信息,最后的分类结果如下图所示(DCNN),十分smooth(平滑),但我们需要的是sharp segmentation。
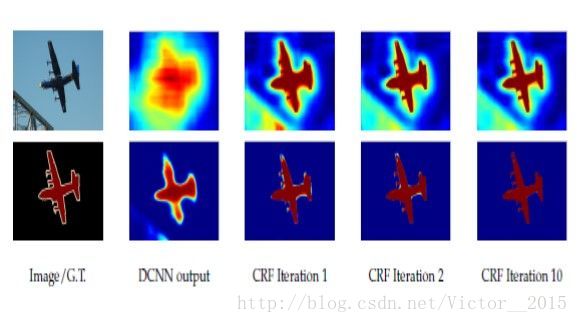
而本文提出的模型令人耳目一新。不仅是之前的dilated conv,而且避开了层层上采样,直接用bilinear interpolation(双线性插值)恢复到原状,(因为deconv逆置卷积没什么卵用),然后进行CRFs通过邻域之间的锐化,得到最终分割结果。
![]()
下面我们给出CRFs的计算公式:
整个模型的能量函数:
其中 x x 是对全局pixels的概率预测分布, xi x i 是其中一个pixel的概率预测分布,而 θi θ i 是一元势函数unary potential function,这里是 θi(xi):=−logP(xi) θ i ( x i ) := − log P ( x i ) ,有点像entropy?
而二元势函数为
K为Kernel数量,w为权重,在本文中采用高斯核,并且任意两个像素点都有此项,故称为fully connected CRFs.
可见二元势函数考虑了原始图片(存疑?还是score map)的像素值和距离。第一个高斯核考虑了both,第二个只考虑了距离。距离越远,像素值相差越大,能量越低。
Deeplab V2: astrous spatial pyramid pooling
![]()
![]()
两图流。v2就是加了ASPP 空洞卷积的空间金字塔。不同dilation的卷积并行操作,然后归一尺寸后求和,仿照R-CNN,效果很好。

