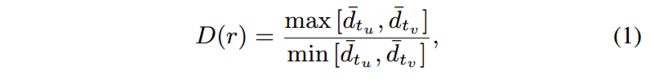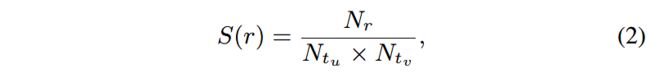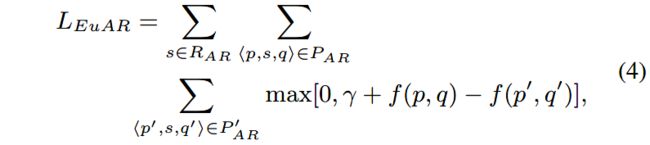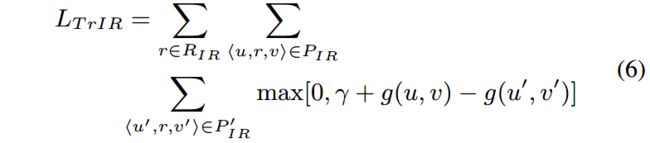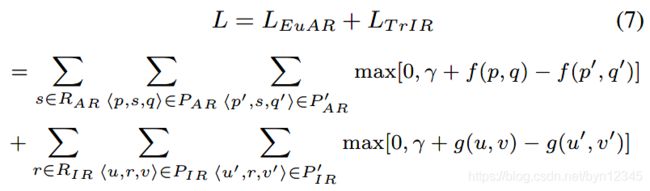【论文解读 AAAI 2019 | RHINE】Relation Structure-Aware Heterogeneous Information Network Embedding
论文链接:https://arxiv.org/abs/1905.08027
代码链接:https://github.com/rootlu/RHINE
会议:AAAI 2019
文章目录
- 1 摘要
- 2 介绍
- 2.1 已有的方法
- 2.2 挑战
- 2.3 作者提出
- 2.4 贡献
- 2.5 一些定义
- 3 关系的结构特征
- 3.1 所属关系(ARs)和交互关系(IRs)
- 4 RHINE模型
- 4.1 基本思想
- 4.2 Different Models for ARs and IRs
- 4.2.1 Euclidean Distance for Affiliation Relations
- 4.2.2 Translation-based Distance for Interaction Relations
- 4.3 A Unified Model for HIN Embedding
- 4.3.1 采样策略
- 5 实验
- 6 总结
1 摘要
现有的HIN嵌入方法大多都是直接将所有关系(relations)都嵌入到单个模型中,而没有区别考虑,这在本质上约束了网络嵌入学习的能力。
本文考虑了异质关联(relations)信息的结构特征,提出RHINE(Relation
structure-aware Heterogeneous Information Network Embedding )模型。
通过对真实的网络进行彻底的数学分析,作者提出了结构相关的衡量标准,将异质关系分为两类:所属关系(Affiliation Relations, ARs)和交互关系(Interaction Relations, IRs)。
作者提出了多个不同的模型,分别处理ARs和IRs,这样可以更好地捕获网络的结构和语义信息。最后将这些模型结合起来,进行优化。
在三个真实数据及上进行了节点聚类、链接预测和节点分类任务,超越了state-of-the-art。
2 介绍
研究的根本问题是HIN的NE问题。
2.1 已有的方法
(1)基于元路径的随机游走获得节点序列,以优化节点间相似度;
(2)将HIN分解成多个简单的网络,在每个子网络中优化节点间相似度;
(3)基于神经网络的方法,为HIN的嵌入学习到非线性的映射函数。
这些方法都是建立在通过让两节点表示间的距离相近,单个模型可以处理所有关系和节点信息。
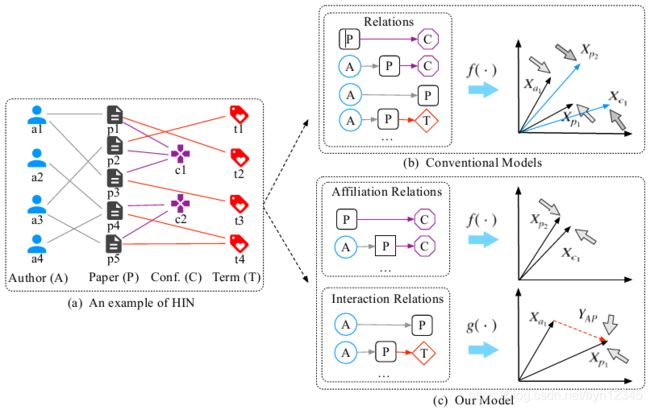
但是HIN中不同类型的边有着不同的结构特征,应该用不同的模型处理它们。如图1(a)所示,网络中有元关系(AP, PC)和组合关系(APA, APC)两种关系。AP和PC就反映了不同的结构特征。AP中作者写了一篇文章,形成了点对点的对等结构;而PC中多篇文章被发表在一个会议中,形成了一对多的结构。
2.2 挑战
考虑HIN中不同关系的特征,面临以下挑战:
(1)如何辨别出HIN中不同关系的结构特征?
(2)如何捕获到HIN中不同类型的结构特征?
(3)建模不同关系的多个模型如何更好地结合,以利于优化?
2.3 作者提出
作者提出RHINE模型以学习HIN的嵌入表示。
首先通过数学分析,将HIN中的关联信息分为两类:一对多的所属关系(ARs, one-centered-by-another),一对一对等的交互关系(IRs, peer-to-peer)。
然后提出两个模型,以捕获不同类型关系的不同结构信息。
对于节点间共享相似属性的ARs,计算节点间的欧式距离作为相似度度量,从而使得两节点在低维空间中距离靠近。
对于连接两兼容节点的IRs,将它们建模为节点之间的转换。
2.4 贡献
(1)是第一个挖掘HIN中的关系,得到不同的结构特征的工作。提出了ARs和IRs,作为区分异质关系的标准。
(2)提出关系结构感知的HIN嵌入学习模型(RHINE),对ARs和IRs建立不同的模型,并统一优化,充分考虑了不同的结构特征。
(3)实验证明了模型的效果,在多个任务(节点聚类、链接预测和节点分类)中优于state-of-the-art。
2.5 一些定义
(1)HIN(异质信息网络)
定义图为 G = ( V , E , T , ϕ , ψ ) G=(V,E,T,\phi,\psi) G=(V,E,T,ϕ,ψ), V V V和 E E E分别是节点集合和边集合。 ϕ ( v ) : V → T V , ψ ( e ) : E → T E \phi(v):V\rightarrow T_V, \psi(e):E\rightarrow T_E ϕ(v):V→TV,ψ(e):E→TE且 ∣ T V ∣ + ∣ T E ∣ > 2 , T = T V ∪ T E |T_V|+|T_E|>2, T=T_V\cup T_E ∣TV∣+∣TE∣>2,T=TV∪TE。
(2)元路径
元路径 m m m是不同类型的边连接起来的不同类型节点的序列,表示两节点之间的复合关系。
(3)node-relation三元组
在图 G G G中,关系 R R R包含元关系和复合关系(元路径)。node-relation三元组 < u , r , v > ∈ P
(4)HIN embedding
输入 G = ( V , E , T , ϕ , ψ ) G=(V,E,T,\phi,\psi) G=(V,E,T,ϕ,ψ),学习到映射 f : V → R d f:V\rightarrow R^d f:V→Rd,将节点 v v v映射成低维的向量表示。
3 关系的结构特征
分析三个HIN中关系的结构特征,在此基础上,提出了两种能够定量区分各种关系的结构相关衡量标准。
文章使用了**DBLP(学术网络)、Yelp(社交网络)和AMiner(学术网络)**三个数据集,并基于元路径分析所有的关系。但是,并不是所有的元路径都能对嵌入学习产生积极的效果,作者根据前人的工作(Shang et al. 2016; Dong, Chawla, and Swami 2017),选取了相对重要的有意义的元路径。
3.1 所属关系(ARs)和交互关系(IRs)
对上述三个数据集进行数学分析。
定义基于节点度的衡量函数 D ( r ) D(r) D(r),以挖掘HIN中不同关系的区别。对于node-relation三元组 < u , r , v >
其中 t u , t r t_u, t_r tu,tr分别是 u , r u, r u,r的节点类型, d t u d_{t_u} dtu和 d t r d_{t_r} dtr分别是类型为 t u , t r t_u, t_r tu,tr的节点的平均度数。
D ( r ) D(r) D(r)值较大时,说明通过关系 r r r连接的两种类型的节点之间,结构不对等,在网络结构中承担的角色不对等,也就是一对多(one-centered-by-another)。此时的关系 r r r体现出了较强的所属关系(ARs),通过这种关系相连的节点,共享更多的相似属性。
若 D ( r ) D(r) D(r)的值较小,则说明两种类型的节点是可兼容的(peer-to-peer)。此时的关系 r r r体现出了较强的交互关系(IRs)。
还可以通过比较关系的稀疏性,捕获结构的差异性信息。根据下式计算出 S ( r ) S(r) S(r),同样可以将关系分为ARs和IRs两类。
其中 N r N_r Nr表示了关系 r r r的实例数, N t u , N t v N_{t_u}, N_{t_v} Ntu,Ntv分别表示类型为 t u , t v t_u, t_v tu,tv的节点数。
显然,所属关系和交互关系展示了不同的特征:
(1)ARs表示一对多的结构,连边两端的不同类型的节点,平均度数差异很大。
(2)IRs表示一对一的对等结构,连边两端的不同类型的节点,平均度数很接近。
4 RHINE模型
提出关系结构感知的HIN嵌入学习模型RHINE,使用不同的模型分别处理ARs和IRs两种关系类型,以保留它们不同的结构特征,如图1©所示。
4.1 基本思想
对于ARs,使用欧氏距离衡量相连的两节点间相似度。有以下两个动机:
(1)ARs表示所属关系,相连的两节点共享相似的属性。因此通过ARs相连的节点在向量空间中应彼此距离近,这和欧氏距离的优化目标相一致。
(2)HIN嵌入学习的目标是保留高阶的相似度信息,满足三角不等式((Hsieh et al. 2017))的欧氏距离,可以保留一阶和二阶的相似度信息。
IRs反映了对等节点间的交互信息。作者将IR建模成节点在低维向量空间的相互转化。基于距离的转化和欧式距离,在数学形式上是一致的,所以两个模型可以很好地结合起来。
4.2 Different Models for ARs and IRs
4.2.1 Euclidean Distance for Affiliation Relations
对于ARs,使用欧氏距离衡量相连的两节点间相似度。给定node-relation三元组 < p , s , q > ∈ P A R
最小化 f ( p , q ) f(p,q) f(p,q),margin-based的损失函数如下:
其中 γ > 0 \gamma>0 γ>0是margin超参, P A R P_{AR} PAR是正样本集, P A R ′ P^{'}_{AR} PAR′是负样本集。
4.2.2 Translation-based Distance for Interaction Relations
给定node-relation三元组 < u , r , v >
其中 X u , X v , Y r X_u, X_v, Y_r Xu,Xv,Yr分别是节点 u , v u, v u,v和关系 r r r的向量表示。
margin-based损失函数定义如下:
其中 P I R P_{IR} PIR是正样本集, P I R ′ P^{'}_{IR} PIR′是负样本集。
4.3 A Unified Model for HIN Embedding
最小化如下的额损失函数,结合两个模型:
4.3.1 采样策略
由于ARs和IRs的分布很不均衡,所以两者的采样比例也不同。根据两者的概率分布,进行正样本的采样。对于正样本 < u , r , v >
5 实验
数据集:DBLP、Yelp、AMiner
实验任务:节点聚类;链接预测;多类分类
对比方法:DeepWalk、LINE、PTE、ESim、HIN2Vec、Metapath2vec
实验结果:
(1)节点聚类实验结果
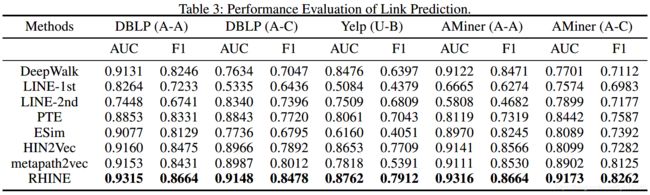
(2)链接预测实验结果
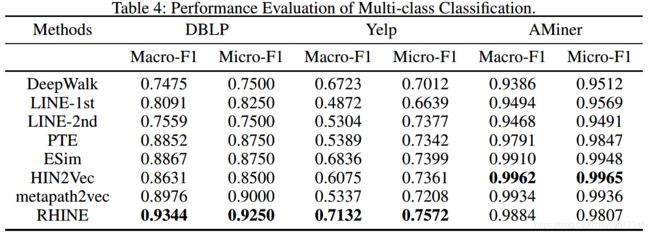
(3)多类分类实验结果
6 总结
本文是第一个在HIN嵌入学习中区别不同关系的不同结构特征。
提出了两个结构相关的衡量标准,用于区别ARs和IRs两类异质关系。提出RHINE模型,分别处理这两类关系,并且在多项任务中超越了state-of-the-art。
未来的研究方向是,发掘出其他可能的衡量方式,以区分不同类型的关系,更好地捕获到HIN中的结构信息。此外,还将研究如何使用深度神经网络,为不同类型的关系建模。
这篇文章的出彩之处在于将不同类型的关系分为了所属关系(ARs)和交互关系(IRs),并给出了数学解释。
而且与以往的将所有节点和关系都建模在一个模型中不同,本文使用了两个模型分别对两种类型的关系进行建模,捕获两类关系蕴含的结构特征,然后再整合。
这两个模型都很简便,没有使用到深度神经网络。