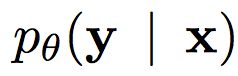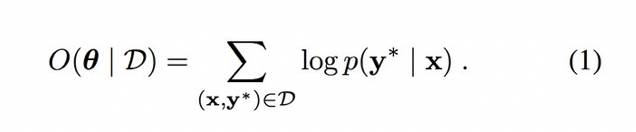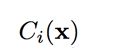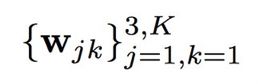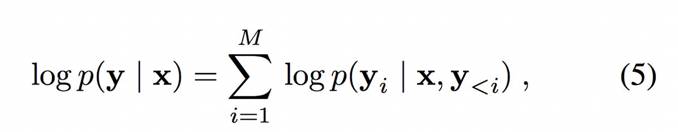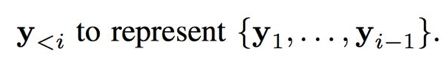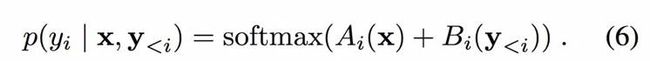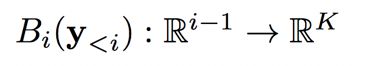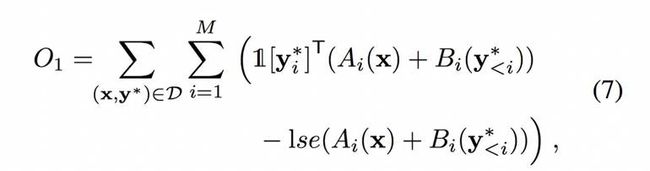谷歌像素递归超分辨率研究:怎么消灭低分辨率图像马赛克?
最近,谷歌发布了一种把低分辨率图像复原为高分辨率图像的方法,参见机器之心文章《》。与最先进的方法相比,这篇论文提出了一种端到端的框架来完成超分辨率任务。它由两个卷积神经网络组成,一个是描述低分辨率图像骨架的优先网络(prior network),一个是用于优化细节特征的调节网络(conditioning network)。这种方法强调了细节特征恢复上的提升,并以概率范式(probabilistic paradigm)的形式提升了其理论。机器之心在本文中对相关研究《Pixel Recursive Super Resolution》的核心算法进行了分析解读,具体将从抽样策略、模型架构和方法分析方面进行叙述。
-
论文地址:https://arxiv.org/pdf/1702.00783.pdf
-
相关报道:https://news.ycombinator.com/item?id=13583476
引言&相关工作
超分辨率问题(Super Resolution Problem)的含义在于恢复图像的分辨率。可用的解决方案能够修复和补充细节补丁来重建高分辨率图像。然而,对于原始图像中不存在的缺失特征,则需要恢复模型来生成它们。因此,最佳的超分辨率恢复模型必须考虑对象、视点、照明和遮挡的复杂变化。它还应该能够画出锐利的边缘,并决定图像不同部分中的纹理、形状和图案呈现类型,因此产生逼真的高分辨率图像是非常困难的。
超分辨率问题在计算机视觉研究中具有悠久的历史。有多种可行的方法来恢复高分辨率图像。其中插值方法易于实现且广泛使用,它基本采用的是对所有合理的细节特征值取均值的策略。然而这类方法的缺点也很明显,因为线性模型不能正确表示输入信息和输出结果之间复杂的依赖关系,所以得到的图像往往是模糊的。
为了获得生动合理的图像细节,研究者已经提出了详细的去模糊(de-blurr)方法。该方法类似于词典构造(dictionary construction,一种相当简单而基本的方法),更进一步是可以在 CNN 中提取多个抽象(CNN 层中存在的特征)的滤波器核(filter kernel)的学习层,然后通过测量被插值的低分辨率图像和高分辨率图像间的像素损失来调整网络权重。基本上这种基于多层过滤器的方法的特征层越多,其表现就越好。因此,该 SRResNet 通过从许多 ResNet 模块中学习来实现预期的性能。这篇论文应用了类似的条件网络设计来更好地处理高频特征。
除了设计高频特征模拟外,下面提出的超分辨率网络模型称为 PixelCNN。PixelCNN 旨在生成低分辨率和高分辨率图像之间的先验知识(prior knowledge)。与另一种生成模型 GAN 相比,当训练样本缺乏分布的多样性时,它们都将受到影响。但超参数更改时,PixelCNN 有更高的稳健性。而 GAN 相当脆弱,只需要足够的重复学习就能愚弄一个不稳定的鉴别器,这样的策略是相当棘手的,于是谷歌超分辨率网络萌芽了。参考下图:
图 3:我们提出的超分辨率网络包含了一个调节网络(conditioning network)和一个优先网络(prior network)。其中调节网络是一个 CNN,其接收低分辨率图像作为输入,然后输出 logits——预测了每个高分辨率(HR)图像像素的条件对数概率(conditional log-probability)。而优先网络则是一个 PixelCNN,其基于之前的随机预测进行预测(用虚线表示)。该模型的概率分布的计算是在来自优先网络和调节网络的两个 logits 集之和上作为 softmax operator 而实现的。
端到端模型由两个网络组成:1. 使用 PixelCNN 的优先网络 2. 使用 ResNet 的 Res 块的调节网络。
方法和实验
在后面的章节中,该论文介绍了像素递归超分辨率(pixel recursive super resolution)框架的优势和像素独立超分辨率(pixel independent super resolution)的潜在问题,并在相应数据集上对这些理论进行了验证,比较了自定义度量。
为了说明部署递归超分辨率方法的必要性,本文首先阐述了像素独立超分辨率方法的理论>下一节将演示这样的理论会在条件图像建模中失败。不理想的实验结果促使谷歌的这个递归模型产生。
基本工作流程显示为:
为了模拟超分辨率问题,其概率目标(probabilistic goal)是学习一个参数模型:
其中 x 和 y 分别表示低分辨率和高分辨率图像。一旦我们获得像素值的调节概率,就可以用高分辨率重建整个图像。我们可以在数据集中应用上述设置,用 y*表示真实的高分辨率图像,从而能在数学上表示成目标函数。优化目标是使条件对数似然度目标(conditional log-likelihood objective)最大化,如下:
关键因素是构建最合适的输出像素值分布。这样我们才能够用锐利的细节得到最生动的高分辨率图像。
像素独立的超分辨率
简单的方式是假设每个预测像素值 y 有条件地独立于其他值,因此总概率 p(y | x)是每个独立估计值的乘积。
假设一幅给定的 RGB 图像具有三个颜色通道,并且每个通道拥有 M 个像素。两边同时取对数得到:
如果我们假设估计的输出值 y 连续,则公式(2)可以在高斯分布模型下重构为:
其中 y_i 表示通过卷积神经网络模型得到的非线性映射输出
,表示第 i 个输出像素的估计平均值。
表示方差,一般来说方差是已知的,而不是通过学习获得的,因此唯一需要学习的是均值和估计值之间的 L2 范数。然后,最大化对数似然(在(1)中表示)可以转化为 y 和 C 之间的 MSE(均方误差)最小化。最后,CNN 能够学习一组高斯参数以获得最佳平均值 C。
对于连续值,我们使用高斯模型,对于离散值,我们使用多项分布来模拟分布(数据集注明为 D),那么预测概率可以描述为:
因此我们的目标是学习以从预测模型中获得最优的 softmax 权值,
是三个通道下 K 个可能的离散像素值的 softmax 权值。
然而,该论文称,上述独立模型无法处理多模式(multi-modality)的情况,因此在某些特定任务中它的性能不如多模态能力方法,例如着色、超分辨率。其次它遵循 MNIST corner dataset 的实验演示(数字仅在左上角或右下角定位对象时相同)。
图 2:上图:图片表示了试验数据集(toy dataset)中输入输出对的一种创建方式****。下图:在这个数据集上训练的几个算法的预测示例。像素独立的 L2 回归和交叉熵模型没有表现出多模态预测。PixelCNN 输出是随机的,且多个样本时出现在每个角的概率各为 50%。
参考 MNIST 实验图,不同方法下的数字生成结果是不同的。像素交叉熵方法可以捕获脆性图像,但无法捕获随机双模态,因此数字对象出现在两个角落。类似的情况发生在 L2 回归方法上。最终在一个高分辨率输出图像中给出两个模糊数字。只有 PixelCNN 可以捕获位置信息和清晰的图像信息,这进一步说明了在所提出的模型中使用 PixelCNN 的优越性。
像素递归超分辨率
像素独立超分辨率方法被指出有局限性之后,它的解释被逐渐给出。新理论仍旨将给定样本 x 的对数似然度最大化。递归模型部分假定输出像素之间存在条件依赖关系。最后,为了近似这种联合分布,该递归方法使用链式法则来分解其条件分布:
其中每个输出有条件地依赖于输入和先前的输出像素:
那么嵌入 CNN 的像素递归超分辨率框架(参考以前的架构)可以说明如下:
输入 x,让
表示调节网络,得到一个对数值组成的向量,这些值是第 i 个输出像素的 K 个可能值的对数。
类似的,让
表示先前网络,得到由第 i 个输出像素的对数值组成的向量。
该方法联合优化两个网络,通过随机梯度上升(stochastic gradient ascend)法更新并获得最大对数似然。也就是说,优化 (6) 中模型预测值与离散的真实值标签之间的交叉熵损失
然后其成本函数为:
其中 lse(·)是 softmax 分母的对数和的指数运算符(log-sum-exp operator),1 [k] 表示一个 K 维 one-hot 指示符向量的第 k 维度设置为 1。
然而,当在实验中使用成本函数时,训练的模型往往忽略调节网络。因此,范式包括一个新的损失项,用于衡量调节网络中预测值和真实值之间的交叉熵,表示为:
从而得到新公式:
除了定义训练的范式,为了控制样本分布的密度,我们引入额外的温度参数(temperature parameter),从而得到了贪婪解码机制(greedy decoding mechanism):总是选择概率最大的像素值和合适的 softmax 中的样本。因此,分布 P 被调整为:
随着所有理论准备工作的完成,本文进入实施阶段。实验在 TensorFlow 框架下完成,使用 8 个带有 SGD 更新的 GPU。对于调节网络,我们建立了前馈卷积神经网络。它使用从一系列 ResNet 块得到的 8×8 RGB 图像和转置卷积层,同时每层保持 32 个通道。最后一层使用 1×1 卷积将信道增加到 256×3,并且使用所得到结果、通过 softmax 算子预测超过 256 个可能子像素值的多项分布。
对于现有网络,通常为像素 CNN,实验使用了每层有 32 个通道的 20 个选通 PixelCNN 层。
结果和评估
为了验证所提框架的性能,本文选择了两类对象:人脸和卧室场景。所有训练图像均来自 CelebA 数据集和 LSUN 卧室数据集。为了满足网络输入的要求,作者还对每个数据集进行了必要的预处理:裁剪 CelebA 数据集的名人脸和 LSUN 卧室数据集的中心图像。此外他们还通过双三次插值(bicubic interpolation)将两个数据集得到的图像大小调整为 32×32,进而为 8×8,构成训练和评估阶段的输出和输入对。
训练后,将递归模型与两个基准网络进行比较:像素独立的 L2 回归(「回归」)和最近邻搜索(「NN」)。视觉效果如下图所示:
观测不同方法之间的结果,能看出 NN 方法可以给出清晰的图像,但是与真实情况的差距相当大,回归模型给出了一个粗略的草图,像素递归超分辨率方法的效果似乎处于两个基准方法之间。它捕获了一些详细的信息,但没有比其他方法好很多。
另外不同的温度参数下,结果略有不同如下图所示:
为了测量性能,我们使用 pSNR 和 MS-SSIM(表 1)量化了训练模型对真实情况的预测精度,除传统测量之外,结果还涉及人类识别研究。
表 1:顶部:在裁切过的 CelebA 测试数据集上,从 8×8 放大到 32×32 后的测试结果。底部:LSUN 卧室。pSNR、SSIM 和 MS-SSIM 测量了样本和 ground truth 之间的图像相似度。Consistency(一致性)表示输入低分辨率图像和下采样样本之间在 [0,1] 尺度上的均方误差(MSE)。% Fooled 表示了在一个众包研究中,算法样本骗过一个人类的常见程度;50% 表示造成了完美的混淆。
从结果表中可以看出,递归模型在 pSNR 和 SSIM 测量中表现不佳。虽然文章还引用了另外两个测量来进行验证。然而,目前在添加合成信息时似乎缺乏强烈的说服力,或者可能需要进一步的工作来测试验证。从逃过人们眼睛的百分比来看,该模型比其它方法更优越,因此可以说生成的图像更加逼真。
总之,像素递归超分辨率方法提出了一个创新的框架来平衡粗略骨架与细节捕获。但是我个人认为,结果不能有力地说明该模型在复原低分辨率图像方面真正有效。虽然不同的分辨率设置使方法难以比较,但它确实能够为人类的判断提供良好表现。因此在未来可能具有良好的工业应用。