HTML5 画布变换

画布变换

Canvas中，默认的坐标系统是以画布的左上角为坐标原点(0, 0)，水平向右为X轴，垂直向下为Y轴，以像素为单位。Canvas在坐标系统上的每个点，都与图形上的一个像素点相对应。如图 4‑30 所示：

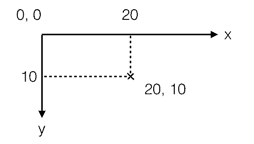图4-30 Canvas的默认坐标系

如果改变Canvas坐标系统的原点，图形也会随之发生改变。针对这一特点，可以通过变换坐标系统来间接操作图形，实现对图形的移动、缩放、旋转。

Canvas的API提供了三种变换坐标系原点的方法：

translate()方法

translate(tx, ty)方法将canvas坐标系的坐标原点向上、下、左、右进行平移。参数tx表示将坐标原点向X轴平移的距离，大于0时向右移动，小于0时向左移动，等于0表示不平移；参数ty表示将坐标原点向Y轴平移的距离，大于0时向下移动，小于0时向上移动，等于0表示不平移。

1. context.fillStyle = "#f00";
2. context.fillRect(0,0,100,100);
4. context.fillStyle = "#0f0";
5. context.translate(100,100);
6. context.fillRect(0,0,100,100);

上述代码，先在canvas中绘制一个红色的矩形，再将Canvas坐标系的坐标原点沿X轴向右平移100px，沿Y轴向下平移100px，然后再绘制一个绿色的矩形。运行效果如图 4‑31 所示：

图4-31 translate()方法坐标系平移

虽然调用fillRect()方法时，两个矩形的位置都是(0, 0)，但从图可以看出，第一个矩形在原来的坐标原点绘制，第二个矩形相对原来的坐标原点向右、向下分别移动了100px，绘制位置为(100, 100)。因为在绘制第二个矩形之前，坐标原点发生了平移。

scale()方法

scale(sx, sy)方法将对canvas坐标系的X轴或Y轴进行缩放。参数sx表示X轴的缩放比例，大于1时放大，小于1时缩小；参数sy表示Y轴的缩放比例，大于1时放大，小于1时缩小。默认情况下，sx 和 sy参数的值均为1，即不进行缩放。

下述代码，将Canvas坐标系的X轴放大1.4倍，Y轴放大1.2倍。

1. context.fillStyle = "#f00";
2. context.fillRect(0, 0, 100, 100);
3. context.fillStyle = "#0f0";
4. context.translate(40, 40);    // 进行平移，防止原来的图形被遮住
5. context.scale(1.4, 1.2);
6. context.fillRect(0, 0, 100, 100);

运行效果如图 4‑32 所示：

图4-32 scale()方法坐标系缩放

使用scale(sx, sy)方法，还可以实现一些实用的效果，如给sx 或 sy赋一个负值，可以实现画布上下文在水平方向或垂直方向上发生翻转，创造出镜像变换的效果。

rotate()方法

rotate(angle)方法将canvas坐标系的坐标原点进行旋转。参数angle表示坐标轴旋转的角度，大于0时顺时针旋转，小于0时逆时针旋转，角度以弧度表示。

下述代码，将canvas坐标系的坐标原点逆时针旋转Math.PI/4。

1. context.fillStyle = "#f00";
2. context.fillRect(50, 50, 100, 100);
4. context.fillStyle = "#0f0";
5. context.rotate(-Math.PI/4);
6. context.fillRect(50, 50, 100, 100);

运行效果如图 4‑33 所示：

图4-33 rotate()方法坐标系旋转

从上图可以看出，默认情况下，rotate()方法的旋转中心是canvas的坐标原点。但是，有时候我们需要绕绕图形自己的中心进行旋转。

如果想要绕图形自己的中心进行旋转，就需要先把坐标原点平移到图形的中心，再进行旋转。坐标原点平移发生后，原图形的坐标也会发生变化。

还是以本例进行说明，canvas的宽度和高度都是200，矩形位于画布的中央，其宽度和高度都是100，故矩形中心点的坐标为(100, 100)，就需要把坐标原点平移到(100, 100)。坐标原点平移后，该矩形的左上角坐标就会跟着发生变化，变为 (-50, -50)。代码如下：

1. context.fillStyle = "#f00";
2. context.fillRect(50, 50, 100, 100);
4. context.fillStyle = "#0f0";
5. context.translate(100, 100);
6. context.rotate(-Math.PI/4);
7. context.fillRect(-50, -50, 100, 100);

这里在rotate()之前调用translate(100, 100)，其目的是将旋转中心从默认点(0，0)移动到矩形的中心点(100, 100)，此时，后面的rotate()就是绕这个点进行旋转。运行效果如图 4‑34 所示：

图4-34 rotate()方法坐标系旋转

说明：

从上面的几个例子可以看到，坐标系的变换，不管是移动、缩放、还是旋转，都只会影响执行变换操作之后的绘制的图形，之前已经绘制的图形不受坐标系变换的影响。

关于作者

歪脖先生，十五年以上软件开发经验，酷爱Web开发，精通 HTML、CSS、JavaScript、jQuery、JSON、Python、Less、Bootstrap等，著有《HTML宝典》、《揭秘CSS》、《Less简明教程》、《JSON教程》、《Bootstrap2用户指南》，并全部在 GitHub 上开源。

版权声明：本文出自 歪脖网 的《HTML宝典》，欢迎在线阅读，并提出宝贵意见。