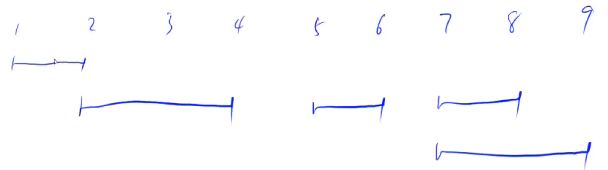AcWing题解——803. 区间合并
题目
题目链接
AcWing OJ：https://www.acwing.com/problem/content/805/。
我的OJ：http://47.110.135.197/problem.php?id=5240。
题目描述
给定 n 个区间 [li, ri]，要求合并所有有交集的区间。 注意如果在端点处相交，也算有交集。
输出合并完成后的区间个数。
例如：[1, 3] 和 [2, 6] 可以合并为一个区间 [1, 6]。
输入
第一行包含整数 n。
接下来 n 行，每行包含两个整数 l 和 r。
输出
共一行，包含一个整数，表示合并区间完成后的区间个数。
样例输入
5
1 2
2 4
5 6
7 8
7 9样例输出
3数据范围
1 ≤ n ≤ 100000,
−10^9 ≤ li ≤ ri ≤10^9。
分析
本题基本和一本通的区间合并一样。只是输出改成了合并后有几个区间。
数学知识
区间一共有两个坐标，即起点坐标和终点坐标。其中起点坐标记为 ST，终点坐标记为 ED。
假设我们有任意两个区间 A 和 B，则这两个区间可以有三种可能关系。
相交
区间 A 和区间 B 有交集，如图所示。
则有这样的数学关系：
。
不相交
区间 A 和区间 B 没有交集，如图所示。
则有这样的数学关系：
。
包含
区间 A 包含区间 B ，如图所示。
则有这样的数学关系：
。
题目分析
本题给定了 n 个区间，要求我们判断这 n 个区间是否可以合并为一个区间。假设有两个区间 A 和 B，这两个区间能合并成一个区间，那么这两个区间的关系只能是上面的相交或者包含。如果区间 A 和区间 B 不相交，则必然不能合并。那么问题就变成如何保证区间 A 在区间 B 的前面，即 
？很简单，将所有区间进行排序，先按照左端点（起点）大小，再按右端点（终点）大小，进行排序即可。
样例数据分析
首先将样例数据排序，变为如下数据：
1 2
2 4
5 6
7 8
7 9我们用下图来表示当前区间状态：
如上图所示，我们可以很清晰的看到，可以合并成 3 个区间，如下图所示。
也就是 [1, 4]、[5, 6] 和 [7, 9] 这三个区间。
区间合并的过程图示可以参考我前面的一个题解，https://blog.csdn.net/justidle/article/details/104553695。
数据范围分析
从题目中可以知道，n 的最大值为 100000，坐标范围是 [-10^9, 10^9]，所以使用 int 表示足够。
对区间的描述，可以使用 STL 的 pair，也可以使用自定义的 struct。
算法思路
1、读入所有数据并保存。
2、将所有区间进行排序。
3、遍历两个相邻区间，看能否合并。如果可以合并，则合并区间，继续遍历直到最后一个区间。如果不可以合并，区间数增加一，继续合并以后的区间。
4、输出最终的区间数。
AC 参考代码
//https://www.acwing.com/problem/content/805/
//区间合并
#include
using namespace std;
//区间定义
struct NODE {
int x;
int y;
};
const int MAXN = 1e5+4;
NODE a[MAXN] = {};
bool mycmp(const NODE &a, const NODE &b) {
if (a.x!=b.x) {
return a.x> n;
int i;
for (i=0; i> a[i].x >> a[i].y;
}
//排序
sort(a, a+n, mycmp);
//遍历
NODE curr = a[0];
int ans = 1;
for (i=1; i curr.y) {
//没有交集
ans++;
curr = a[i];
} else {
//包含或者相交关系
curr.y = max(curr.y, a[i].y);
}
}
cout << ans << endl;
return 0;
}