C/C++生成固定范围随机数的问题
在C/C++中,rand函数可以产生[0, 32767]之间的伪随机整数,且服从均匀分布,意思就是说产生[0, 32768)之间任意一个整数的概率为1/32768.
但是绝大多数,我们想得到在某个范围(比如0-100)之间的随机数。我们同样希望在这个范围产生的随机数也能够服从均匀分布,也就是说产生每个数的概率相等。在网络上我们经常会看到这样的例子:
x = rand()%100; //产生[0, 100)之间的随机整数可能我们会不经意的认为,我们产生的随机数也在这个区间服从均匀分布,即我们所产生的[0, 100)中的每个数的概率是一样的。真的是这样吗?当然不是!你可能会感觉有点小小诧异,但是你只要稍稍想象一下,把[0, 32768)按照100的模分割成327份100再加上最后剩下的68,很明显可以感觉出来,在区间[0, 68)和[68, 100)之间生产的随机数的概率肯定不太一样。这样说也许你很不服气,那么就通过数学知识来严格证明一下。
为了证明方便,这里我假设区间是连续的了。那么问题就转换成:
已知X~U[0, 32768),求Y=X%100服从的分布和概率密度。
所以生成[0,68)之间的数的概率为328/32768*68,生成[68,100)之间的数的概率为327/32768*32
对于离散量来说,产生0到67之间的整数的概率是一样的,所以,产生0到67之间的整数概率为:
产生68到99之间的整数概率是一样的,所以,产生68到99之间的整数概率为 :
有没有大吃一惊?或许你觉得没什么的,毕竟这两者之间概率都差不多,可是有时候,这种差不多思想可能会付出惨重的代价。理论上也证明了,下面看看在程序中是如何体现的吧!以下是一段C/C++代码:
#include "time.h"
#include
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
srand((unsigned)time(NULL));
int num[100] = {0};
for (int i = 0; i < 100000000; ++i)
{
int x = rand()%100;
++num[x];
}
for (int i = 0; i < 100; ++i)
{
cout << i << ": " << (double)num[i]/100000000 << endl;
}
getchar();
return 0;
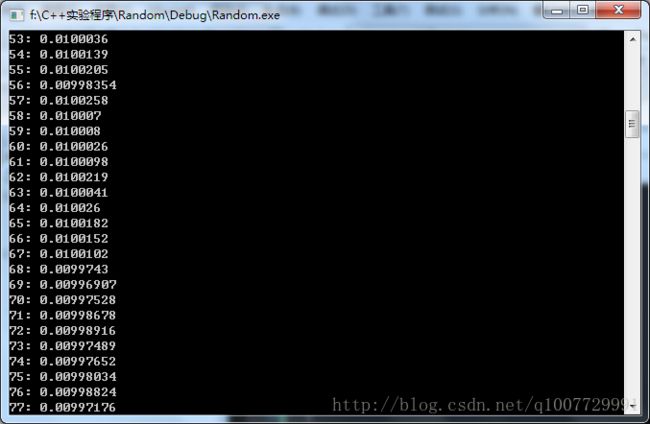
} 以下是在我的机器上运行的结果:
67与68之间形成一道十分明显的分水岭。
说了这么多废话,那要如何改进这个问题呢?其实在MSDN中都已经为我们做好,其中有一个小Demo是这样写的:
void RangedRandDemo( int range_min, int range_max, int n )
{
// Generate random numbers in thehalf-closed interval
// [range_min, range_max). In other words,
// range_min <= random number 这个函数可以生成[range_min,range_max)之间的随机数,而且生成的数的概率也是完全一样的。还在犹豫什么呢?赶紧试试吧!
第一次写博客,希望小伙伴们多指正哦!