机械手基础知识（3）之基于图像的视觉伺服与基于位置的视觉伺服

**

基于图像的视觉伺服与基于位置的视觉伺服

**

有关于机械手位姿问题的理解，可以去看我关于机械手正逆运动学分析的文章

首先说，基于图像的视觉伺服与基于位置的视觉伺服主要表现形式在于图像雅可比矩阵的构建机器表现形式。
其实，关于视觉伺服的一些知识，还是有必要了解的。不然文章和方法看了好多，最后还不知道人家用的是基于图像的方法，还是基于位置的方法，这样你会在圈里转，单纯通过数学的方法理解人家给出的雅可比矩阵，我相信在座的各位没几个有那个本事，所以如果是新手，还是建议看完这个。彻底理解这两个概念在去看论文，看代码。

1. 基础知识—视觉伺服的基本思想

------基于视觉的伺服控制方法的目的是最小化一个图像误差，该误差可以定义为：
--------------------------------- $e(t)=s(m(t),a)-s^{\ast }$ --------------------------- (1)
------式(1)为视觉伺服控制方法的通用形式。其中$m(t)$是一系列的图像特征，如图像点特征、形状特征、位姿特征或频域特征等。 $s(m(t),a)$表示通过特征$m(t)$与一些额外的系统参数构成的映射函数。将提取的特征$m(t)$映射至目标特征$s^{\ast }$的空间中，并与$s^{\ast }$进行比较，当两者差为零时，即系统误差$e(t)$为零，系统迗到稳定的收敛位置。
------视觉伺服方法的不同主要体现在设计不同的目标图像特征$s$。其中最经典的方法包括基于图像的视觉伺服以及基于位置的视觉伺服。基于图像的视觉伺服方法通过从图像中获取的特征点直接控制机械臂的运动，而基于位置的伺服方法首先通过图像特征点计算目标的位姿，再根据机械臂与目标物体的相对位姿规划运动方案。一旦确定了图像特征$s$的选择，即可确定控制器的设计形式。最筒单的控制方法是设计一个速度控制器来控制机械臂的移动。为了得到图像特征$s$随时间的变化率与摄像机运动速度的关系，设摄像机在摄像机坐标系下的瞬时速度为${\mathbf{v}}_c=(v_c,{\omega }_c)$，其中$v_c$为在摄像机坐标系下的瞬时线速度，${\omega }_c$为摄像机坐标系下的瞬时角速度。则图像特征随时间的变化率$\dot{s}$与摄像机速度${\mathbf{v}}_c$的关系可以表示为：
------------------------------------$\dot{s}={\mathbf{L}}_s{\mathbf{v}}_{{}_c}$ ---------------------------- (2)

------其中${\mathbf{L}}_s\in {\mathbb{R}}^{k\times 6}$为图像雅克比矩阵。将式(2)代入(1)可得：
-----------------------------------$\dot{e}={\mathbf{L}}_e{\mathbf{v}}_c$ ---------------------------- (3)

------其中${\mathbf{L}}_e={\mathbf{L}}_s$,考虑将${\mathbf{v}}_c$作为机械臂速度控制的输入，并保证图像误差的指数型下降，则可以通过对公式(3)中的雅克比矩阵求逆得到：
---------------------------------${\mathbf{v}}_c=-\lambda {\mathbf{L}}_e^{+}\mathbf{e}$--------------------(4)
------其中${\mathbf{L}}_e^{+}\in {\mathbb{R}}^{6\times k}$是${\mathbf{L}}_e$的伪逆，即当矩阵${\mathbf{L}}_e$为非方阵或奇异时，${\mathbf{L}}_e^{+}=({\mathbf{L}}_e^T{\mathbf{L}}_e{)}^{-1}{\mathbf{L}}_e^T$。在实际的视觉伺服系统中，在控制阶段的每一时刻获得精确的${\mathbf{L}}_e$或者${\mathbf{L}}_e^{+}$是十分困难的。因此需要对图像雅克比矩阵进行估计。因此实际的视觉伺服控制方程应改写为：
---------------------------------${\mathbf{v}}_c=-\lambda {\hat{\mathbf{L}}}_e^{+}\mathbf{e}$--------------------(5)
式(5)为视觉伺服控制的基本公式，在此公式的基础上，仅需要考虑三个问题来设计视觉伺服控制的方程：(1)如何选择图像特征$s$。(1)基于图像特征$s$的雅克比矩阵${\mathbf{L}}_s$如何推导；(3)${\hat{\mathbf{L}}}_e^{+}\mathbf{e}$如何估计

好了，这些都是小意思，下面开始讲重点了。

2. 基于图像的视觉伺服

------基于图像的视觉伺服，其误差信号直接用图像特征来定义图象平面坐标（非任务空间坐标）的函数。其基本原理是由该误差信号计算出控制量，并将其变换到机器人运动空间中去，从而驱动机械手向目标运动，完成伺服任务。对于抓取静止目标的任务，该误差仅是机械手图像特征的函数；对于运动目标，误差还是运动目标图像特征的函数。该方法无需估计目标在笛卡儿坐标系中的位姿，减少了计算时延，并可克服摄像机标定误差及关节位置传感器误差对定位精度的影响。然而，为了将图像特征参数的变化同机器人位姿变化联系起来，该方法必须计算图像雅可比矩阵（Image Jacobian Matrix）及其逆矩阵。基于图像的视觉伺服本质上是把伺服任务放在图像特征参数空间中进行描述和控制。
------基于图像的视觉伺服系统的定位精度对摄像机标定误差不敏感。与基于位置的视觉伺服相比， 具有较少的计算量。 文献通过仿真与实验表明， 对于 eye in hand 构型的机器人视觉伺服系统，在存在图像量化误差、摄像机标定误差和图像噪声的情况下，基于图像的伺服方式比基于位置的伺服方式有更好的定位与跟踪效果。

------传统的基于图像的视觉飼服方式使用一系列特征点作为图像控制特征来定义$s$。对图像的测量$m(t)$通常是对应特征点对在图像上的像素距离，而系统参数$a$为摄像机的内参数。基于这祥的设定，可定义在摄像机坐标系下的空间点$\mathbf{X}=\left\{X,Y,Z\right\}$，它在摄像机二维成像平面上所映射的点为$\mathbf{x}=\left\{x,y\right\}$。则可以得到：

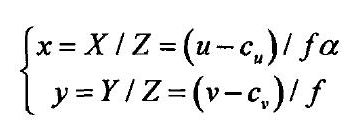
-----------------------------------------------------------------------------------------(6)
------其中$m=(u,v)$表示在图像坐标系下以像素为单位的点，$a=\left\{c_u,c_v,f,\alpha \right\}$为摄像机的内参数。$c_u$和$c_u$分别表示图像坐标系下光心点的$x$轴方向与$y$轴方向的坐标，$f$表示摄像机的焦距，$\alpha$是摄像机像素长宽比因子。令$s=\mathbf{x}=(x,y)$，即以图像坐标系下特征点的坐标作为图像控制特征。对式(6)进行求导有：

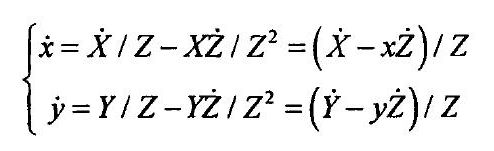
--------------------------------------------------------------------------------------------------(7)
-------将三维空间点的速度与摄像机的速度联系起来有：

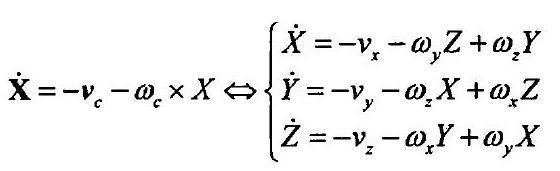
----------------------------------------------------------------------------------------------------------(8)
将式(8)代入式(7)可整理得到：

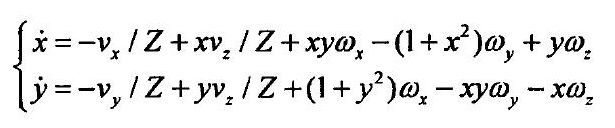
-----------------------------------------------------------------------------------------------------------(9)
基于上式的控制方程可写为：
------------------------------------------$\dot{\mathbf{x}}={\mathbf{L}}_{\mathbf{x}}{\mathbf{v}}_{\mathbf{c}}$----------------------------------------------------------(10)
其中关于图像特征$\mathbf{x}$的图像雅克比矩阵为：

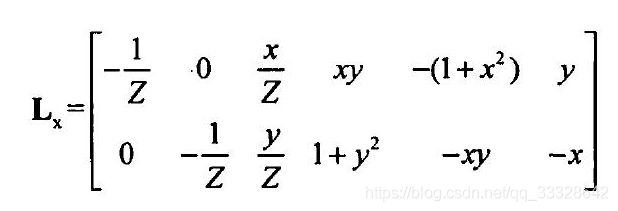
-----------------------------------------------------------------------------------(11)
------在图像雅克比矩阵中，Z的值是特征点在摄像机坐标系下的深度。因此，任何使用基于图像特征点的视觉伺服控制方法均需要对Ｚ进行估计。另一方面，$x$和$y$的计算涉及到了摄像机的内参数，因此不能直接将式(11)代入式(4)形成控制方程，而需要对$\dot{\mathbf{x}}$进行估计获得$\widehat{{\mathbf{L}}_{\mathbf{x}}}$
------为了控制机械臂的六个自由度，至少需要三个特征点组成秩为６的图像雅克比矩阵。例如使用特征向量$\mathbf{x}=\left(x_1,x_2,x_3\right)$，则可获得图像雅克比矩阵：

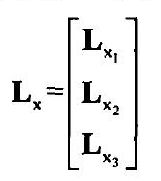
------------------------------------------------------------------------(12)
------但在这种情况下，当控制点特征运动到特定位置时图像雅克比矩阵会出现奇异性问题。另外，对于仅依靠３个图像特征点的控制，在这个运动空间中存在４个全局最小值，并且难以相互区分。因此在实际应用中常考虑采用特征点的数目大于３。
------选择好控制特征后，另一个核心问题是如何估计控制方程中的${\hat{\mathbf{L}}}_e^{+}$，最理想的情况是令${\hat{\mathbf{L}}}_e^{+}={\mathbf{L}}_e^{+}$，根据式(11)所得结果，需要在迭代控制过程中的每一步估计当前特征点深度的值Ｚ。但在每次迭代时估计Ｚ的值是十分耗时的方式，因此在设计控制方程时可以选择近似的图像雅克比矩阵。
------常用的雅克比矩阵估计的选择有：(1)${\hat{\mathbf{L}}}_e^{+}={\mathbf{L}}_{e^{\ast }}^{+}$其中${\mathbf{L}}_{e^{\ast }}^{+}$是当机械臂运动到基准位置时${\mathbf{L}}_e^{}$的值，即$e=e^{\ast }=0$；${\hat{\mathbf{L}}}_e^{+}=1/2{({\mathbf{L}}_{\mathbf{e}}+{\mathbf{L}}_{{\mathbf{e}}^{\ast }})}^{+}$，虽然这种方法提供了更好的运动轨迹，但由于方程中包含了${\mathbf{L}}_{\mathbf{e}}$因此需要在每步迭代过程中估计目标特征点的深度信息。

3. 基于位置的视觉伺服

------基于位置的视觉伺服，其反馈信号在三维任务空间中以直角坐标形式定义。基本原理是通过对图像特征的提取，并结合已知的目标几何模型及摄像机模型，三维笛卡尔坐标系中对目标位姿进行估计，然后由机械手当前位姿与目标位姿之差，进行轨迹规划并计算出控制量，驱动机械手向目标运动，最终实现定位、抓取功能。目前，多数视觉伺服系统采用基于位置的控制方式
------基于位置的视觉伺服控制系统的定位精度在很大程度上依赖于目标位姿的估计精度，但位姿计算与手眼系统参数标定有关，因此要保证这一估计过程的准确度是十分困难的。在某些情况下，基于位置的控制对标定参数误差十分敏感。

------基于位置的视觉伺服方法利用摄像机与物体的相对位姿作为控制特征$s$。因此控制特征$s$可以参数化的表示为相机相对于目标物体的相对位姿。由于对位姿的估计需要目标物体的三维模型以及相机的内参数，因此基于位置的视觉伺服中的系统参数$a$包含这两个部分。为表述方便，令当前相机坐标系为${\mathbf{F}}_{\mathbf{c}}$，期望的相机坐标系为${\mathbf{F}}_{{\mathbf{c}}^{\ast }}$以及与目标物体坐标系为${\mathbf{F}}_{\mathbf{o}}$。并采用标准的坐标系相关表示法对变换矩阵进行定义。令${}_{}^c{\text{t}}_o$与${}_{}^{c^{\ast }}{\text{t}}_o$分别表示相对于当前摄像机坐标系与期望的摄像机坐标系下，观测到的目标物体坐标系的平动向量。同时，令$\mathbf{R}={}_{}^{{\mathbf{c}}^{\ast }}{\text{R}}_{\mathbf{c}}$表示相机坐标系与基坐标系之间的旋转矩阵。
------在此基准下，可定义$\mathbf{s}=\left(\mathbf{t},\theta \mathbf{u}\right)$其中$\mathbf{t}$是平移向量，$\theta \mathbf{u}$是旋转角的参数化表示。若将$\mathbf{t}$定义为相机坐标系对于物体坐标系之间的距离，则$\mathbf{s}=\left({}_{}^{\mathbf{c}}{\text{t}}_{\mathbf{o}},\theta \mathbf{u}\right)$，${\mathbf{s}}^{\ast }=\left({}_{}^{{\mathbf{c}}^{\ast }}{\text{t}}_{\mathbf{o}},0\right)$，$\mathbf{e}={(}_{}^{\mathbf{c}}{\text{t}}_0{-}_{}^{{\mathbf{c}}^{\ast }}{\text{t}}_0,\theta \mathbf{u})$。关于误差$e$的图像雅克比矩阵可以表示为：

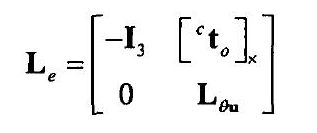
-----------------------------------------------------------------------------------------(13)
其中，${\mathbf{I}}_3$为３ｘ３单位矩阵则通过罗德里格斯公式推导得到:

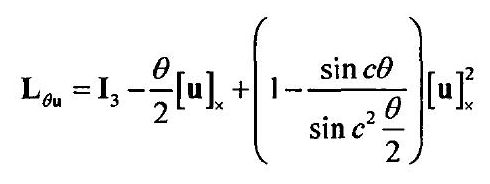
--------------------------------------------------------------------------------------------------(14)
------其中，$sinc$函数的定义为；$xsincx＝sinx$ 且$sinc0=1$。根据式(4)的形式可得基于位置视觉伺服的控制方程为：

由于图像雅克比矩阵为一个秩为６的方阵，可以直接计算图像雅克比矩阵的逆：

-----------------------------------------------------------------------------------------------------------(15)
由于${\mathbf{L}}_{\theta \mathbf{u}}^{-1}=\theta \mathbf{u}$，因此可以推得线速度与角速度的离散表达形式

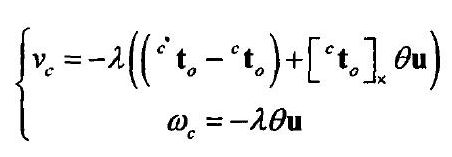
------由此可见，视觉伺服技术的核心思想是通过选定一组特定的图像特征，并推导选定的图像特征与摄像机运动速度之间的关系，即图像雅克比矩阵，到图像特征达到基准的状态时，摄像机的运动速度也同时收敛至零，这时机械臂运动到指定的目标位置。基于图像特征点的视觉伺服方法虽然不需要估计目标物体的位姿，仅通过特征点的匹配即可控制相机的移动，但过于依赖特征点的获取，对于低纹理的目标难以适用。基于位置的视觉伺服方法重点在于目标物体位姿识别的一致性，若对不同的图像特征下的目标物体识别出同样的位姿，则会导致基于位置的视觉伺服的失败。

参考文献

[1]Chaumette F , Hutchinson S . Visual servo control, Part I: Basic approaches[J]. IEEE Robotics & Automation Magazine, 2006, 13.