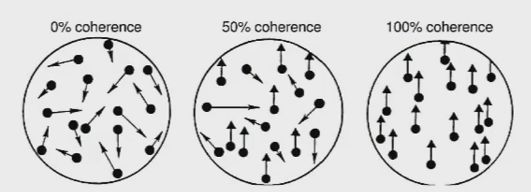
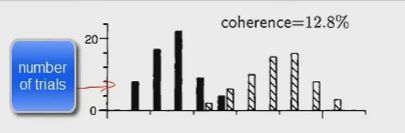
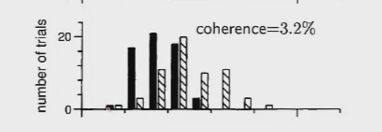
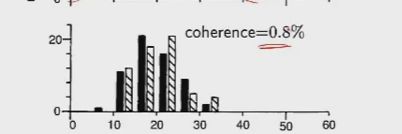
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- ArcGIS栅格计算器常见公式(赋值、0和空值的转换、补充栅格空值)
研学随笔
arcgis经验分享
我们在使用ArcGIS时通常经常用到栅格计算器,今天主要给大家介绍我日常中经常用到的几个公式,供大家参考学习。将特定值(-9999)赋值为0,例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值(如0)Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值,其他保留原值SetNull("raster"==
- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- 每日一题——第九十题
互联网打工人no1
C语言程序设计每日一练c语言
题目:判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串,对每个可能得
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
- 398顺境,逆境
戴骁勇
2018.11.27周二雾霾最近儿子进入了一段顺境期,今天表现尤其不错。今天的数学测试成绩喜人,没有出现以往的计算错误,整个卷面书写工整,附加题也在规定时间内完成且做对。为迎接体育测试的锻炼有了质的飞跃。坐位体前屈成绩突飞猛进,估测成绩能达到12cm,这和上次测试的零分来比,简直是逆袭。儿子还在不断锻炼和提升,唯恐到时候掉链子。跑步姿势在我的调教下,逐渐正规起来,速度随之也有了提升。今晚测试的50
- 在一台Ubuntu计算机上构建Hyperledger Fabric网络
落叶无声9
区块链超级账本Hyperledgerfabric区块链ubuntu构建hyperledgerfabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台,为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时,我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件,部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
- GitHub上克隆项目
bigbig猩猩
github
从GitHub上克隆项目是一个简单且直接的过程,它允许你将远程仓库中的项目复制到你的本地计算机上,以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南,帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前,你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统,用于跟踪和管理代码变更。你可以从Git的官方网站(https://git-scm.
- Day1笔记-Python简介&标识符和关键字&输入输出
~在杰难逃~
Pythonpython开发语言大数据数据分析数据挖掘
大家好,从今天开始呢,杰哥开展一个新的专栏,当然,数据分析部分也会不定时更新的,这个新的专栏主要是讲解一些Python的基础语法和知识,帮助0基础的小伙伴入门和学习Python,感兴趣的小伙伴可以开始认真学习啦!一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码,再通过语言处理程序执行向计算机发送指令,让计算机完成对应的工作,编程
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题)
寻找你83497
k均值聚类算法考试例题
?算法:第一步:选K个初始聚类中心,z1(1),z2(1),…,zK(1),其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定,例如可选开始的K个.k均值聚类:---------一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;模糊的c均值聚类算法:--------一种模糊聚类算法,是.K均值聚类算法是先随机选取K个对象作为初始的聚类
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- Shell、Bash、Zsh这都是啥啊
小白码上飞
bashlinux开发语言
Zsh和Bash都是我们常用的Shell,那先搞明白啥是shell吧。Shell作为一个单词,他是“壳”的意思,蛋壳坚果壳。之所以叫壳,是为了和计算机的“核”来区分,用它表示“为使用者提供的操作界面”。所以这个命名其实很形象,翻译成中文,直译过来叫“壳层”。个人认为这个叫法很奇怪,意译貌似也没有什么好的词汇来匹配。就还是叫shell吧。维基百科给的定义是:Incomputing,ashellisa
- ExpRe[25] bash外的其它shell:zsh和fish
tritone
ExpRebashlinuxubuntushell
文章目录zsh基础配置实用特性插件`autojump`语法高亮自动补全fish优点缺点时效性本篇撰写时间为2021.12.15,由于计算机技术日新月异,博客中所有内容都有时效和版本限制,具体做法不一定总行得通,链接可能改动失效,各种软件的用法可能有修改。但是其中透露的思想往往是值得学习的。本篇前置:ExpRe[10]Ubuntu[2]准备神秘软件、备份恢复软件https://www.cnblogs
- 简单了解 JVM
记得开心一点啊
jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称,意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统(如:JVM、VMwave、VirtualBox)。JVM和其他两个虚拟机
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- 语文主题教学学习笔记之87
东哥杂谈
“语文主题教学”学习笔记之八十七(0125)今天继续学习小学语文主题教学的实践样态。板块三:教学中体现“书艺”味道。作为四大名著之一的《水浒传》,堪称我国文学宝库之经典。对从《水浒传》中摘选的单元,教师就要了解其原生态,即评书体特点。这也要求教师要了解一些常用的评书行话术语,然后在教学时适时地加入一些,让学生体味其文本中原有的特色。学生也要尽可能地通过朗读的方式,而不单是分析讲解的方式进行学习。细
- Python神器!WEB自动化测试集成工具 DrissionPage
亚丁号
python开发语言
一、前言用requests做数据采集面对要登录的网站时,要分析数据包、JS源码,构造复杂的请求,往往还要应付验证码、JS混淆、签名参数等反爬手段,门槛较高。若数据是由JS计算生成的,还须重现计算过程,体验不好,开发效率不高。使用浏览器,可以很大程度上绕过这些坑,但浏览器运行效率不高。因此,这个库设计初衷,是将它们合而为一,能够在不同须要时切换相应模式,并提供一种人性化的使用方法,提高开发和运行效率
- 计算机木马详细编写思路
小熊同学哦
php开发语言木马木马思路
导语:计算机木马(ComputerTrojan)是一种恶意软件,通过欺骗用户从而获取系统控制权限,给黑客打开系统后门的一种手段。虽然木马的存在给用户和系统带来严重的安全风险,但是了解它的工作原理与编写思路,对于我们提高防范意识、构建更健壮的网络安全体系具有重要意义。本篇博客将深入剖析计算机木马的详细编写思路,以及如何复杂化挑战,以期提高读者对计算机木马的认识和对抗能力。计算机木马的基本原理计算机木
- 4 大低成本娱乐方式: 小说, 音乐, 视频, 电子游戏
穷人小水滴
娱乐音视频低成本小说游戏
穷人如何获得快乐?小说,音乐,视频,游戏,本文简单盘点一下这4大低成本(安全)娱乐方式.这里是穷人小水滴,专注于穷人友好型低成本技术.(本文为58号作品.)目录1娱乐方式1.1小说(网络小说)1.2音乐1.3视频(b站)1.4游戏(电子游戏/计算机软件)2低成本:一只手机即可3总结与展望1娱乐方式这几种,也可以说是艺术的具体形式.更专业的说,(娱乐)是劳动力再生产的重要组成部分.使人放松,获得快乐
- 计算机网络八股总结
Petrichorzncu
八股总结计算机网络笔记
这里写目录标题网络模型划分(五层和七层)及每一层的功能五层网络模型七层网络模型(OSI模型)==三次握手和四次挥手具体过程及原因==三次握手四次挥手TCP/IP协议组成==UDP协议与TCP/IP协议的区别==Http协议相关知识网络地址,子网掩码等相关计算网络模型划分(五层和七层)及每一层的功能五层网络模型应用层:负责处理网络应用程序,如电子邮件、文件传输和网页浏览。主要协议包括HTTP、FTP
- matlab delsat = setdiff(1:69,unique(Eph(30,:))); 语句含义
黄卷青灯77
matlab开发语言setdiff
这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下:delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量,包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
- #千锋逆战班 郭燕 学习的一天开启
郭千岁呗
在千锋"逆战"学习云计算第17天加油努力会有好结果复习昨天知识中国加油!武汉加油!千峰加油!我自己加油!
- 《转介绍方法论》学习笔记
小可乐的妈妈
一、高效转介绍的流程:价值观---执行----方案一)转介绍发生的背景:1、对象:谁向谁转介绍?全员营销,人人参与。①员工的激励政策、客户的转介绍诱因制作客户画像:a信任;支付能力;意愿度;便利度(根据家长具备四个特征的个数分为四类)B性格分类C职业分类D年龄性别②执行:套路,策略,方法,流程2、诱因:为什么要转介绍?认同信任;多方共赢;传递美好;零风险承诺打动人心,超越期待。选择做教育,就是选择
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 计算机毕业设计PHP仓储综合管理系统(源码+程序+VUE+lw+部署)
java毕设程序源码王哥
php课程设计vue.js
该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流项目运行环境配置:phpStudy+Vscode+Mysql5.7+HBuilderX+Navicat11+Vue+Express。项目技术:原生PHP++Vue等等组成,B/S模式+Vscode管理+前后端分离等等。环境需要1.运行环境:最好是小皮phpstudy最新版,我们在这个版本上开发的。其他版本理论上也可以。2.开发
- 经纬恒润二面&三七互娱一面&元象二面
Redstone Monstrosity
面试前端
1.请尽可能详细地说明,进程和线程的区别,分别有哪些应用场景?进程间如何通信?线程间如何通信?你的回答中不要写出示例代码。进程和线程是操作系统中的两个基本概念,它们在计算机系统中扮演着不同的角色,并且在不同的应用场景中发挥作用。进程和线程的区别定义:进程:进程是操作系统进行资源分配和调度的基本单位。每个进程都有独立的内存空间和系统资源。线程:线程是进程内的一个执行单元,是操作系统进行调度的最小单位
- AI大模型的架构演进与最新发展
季风泯灭的季节
AI大模型应用技术二人工智能架构
随着深度学习的发展,AI大模型(LargeLanguageModels,LLMs)在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进,包括从Transformer的提出到GPT、BERT、T5等模型的历史演变,并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍:Transformer的核心原理Transformer架构的背景在Transfo
- Spring4.1新特性——综述
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- Schema与数据类型优化
annan211
数据结构mysql
目前商城的数据库设计真是一塌糊涂,表堆叠让人不忍直视,无脑的架构师,说了也不听。
在数据库设计之初,就应该仔细揣摩可能会有哪些查询,有没有更复杂的查询,而不是仅仅突出
很表面的业务需求,这样做会让你的数据库性能成倍提高,当然,丑陋的架构师是不会这样去考虑问题的。
选择优化的数据类型
1 更小的通常更好
更小的数据类型通常更快,因为他们占用更少的磁盘、内存和cpu缓存,
- 第一节 HTML概要学习
chenke
htmlWebcss
第一节 HTML概要学习
1. 什么是HTML
HTML是英文Hyper Text Mark-up Language(超文本标记语言)的缩写,它规定了自己的语法规则,用来表示比“文本”更丰富的意义,比如图片,表格,链接等。浏览器(IE,FireFox等)软件知道HTML语言的语法,可以用来查看HTML文档。目前互联网上的绝大部分网页都是使用HTML编写的。
打开记事本 输入一下内
- MyEclipse里部分习惯的更改
Array_06
eclipse
继续补充中----------------------
1.更改自己合适快捷键windows-->prefences-->java-->editor-->Content Assist-->
Activation triggers for java的右侧“.”就可以改变常用的快捷键
选中 Text
- 近一个月的面试总结
cugfy
面试
本文是在学习中的总结,欢迎转载但请注明出处:http://blog.csdn.net/pistolove/article/details/46753275
前言
打算换个工作,近一个月面试了不少的公司,下面将一些面试经验和思考分享给大家。另外校招也快要开始了,为在校的学生提供一些经验供参考,希望都能找到满意的工作。
- HTML5一个小迷宫游戏
357029540
html5
通过《HTML5游戏开发》摘抄了一个小迷宫游戏,感觉还不错,可以画画,写字,把摘抄的代码放上来分享下,喜欢的同学可以拿来玩玩!
<html>
<head>
<title>创建运行迷宫</title>
<script type="text/javascript"
- 10步教你上传githib数据
张亚雄
git
官方的教学还有其他博客里教的都是给懂的人说得,对已我们这样对我大菜鸟只能这么来锻炼,下面先不玩什么深奥的,先暂时用着10步干净利索。等玩顺溜了再用其他的方法。
操作过程(查看本目录下有哪些文件NO.1)ls
(跳转到子目录NO.2)cd+空格+目录
(继续NO.3)ls
(匹配到子目录NO.4)cd+ 目录首写字母+tab键+(首写字母“直到你所用文件根就不再按TAB键了”)
(查看文件
- MongoDB常用操作命令大全
adminjun
mongodb操作命令
成功启动MongoDB后,再打开一个命令行窗口输入mongo,就可以进行数据库的一些操作。输入help可以看到基本操作命令,只是MongoDB没有创建数据库的命令,但有类似的命令 如:如果你想创建一个“myTest”的数据库,先运行use myTest命令,之后就做一些操作(如:db.createCollection('user')),这样就可以创建一个名叫“myTest”的数据库。
一
- bat调用jar包并传入多个参数
aijuans
下面的主程序是通过eclipse写的:
1.在Main函数接收bat文件传递的参数(String[] args)
如: String ip =args[0]; String user=args[1]; &nbs
- Java中对类的主动引用和被动引用
ayaoxinchao
java主动引用对类的引用被动引用类初始化
在Java代码中,有些类看上去初始化了,但其实没有。例如定义一定长度某一类型的数组,看上去数组中所有的元素已经被初始化,实际上一个都没有。对于类的初始化,虚拟机规范严格规定了只有对该类进行主动引用时,才会触发。而除此之外的所有引用方式称之为对类的被动引用,不会触发类的初始化。虚拟机规范严格地规定了有且仅有四种情况是对类的主动引用,即必须立即对类进行初始化。四种情况如下:1.遇到ne
- 导出数据库 提示 outfile disabled
BigBird2012
mysql
在windows控制台下,登陆mysql,备份数据库:
mysql>mysqldump -u root -p test test > D:\test.sql
使用命令 mysqldump 格式如下: mysqldump -u root -p *** DBNAME > E:\\test.sql。
注意:执行该命令的时候不要进入mysql的控制台再使用,这样会报
- Javascript 中的 && 和 ||
bijian1013
JavaScript&&||
准备两个对象用于下面的讨论
var alice = {
name: "alice",
toString: function () {
return this.name;
}
}
var smith = {
name: "smith",
- [Zookeeper学习笔记之四]Zookeeper Client Library会话重建
bit1129
zookeeper
为了说明问题,先来看个简单的示例代码:
package com.tom.zookeeper.book;
import com.tom.Host;
import org.apache.zookeeper.WatchedEvent;
import org.apache.zookeeper.ZooKeeper;
import org.apache.zookeeper.Wat
- 【Scala十一】Scala核心五:case模式匹配
bit1129
scala
package spark.examples.scala.grammars.caseclasses
object CaseClass_Test00 {
def simpleMatch(arg: Any) = arg match {
case v: Int => "This is an Int"
case v: (Int, String)
- 运维的一些面试题
yuxianhua
linux
1、Linux挂载Winodws共享文件夹
mount -t cifs //1.1.1.254/ok /var/tmp/share/ -o username=administrator,password=yourpass
或
mount -t cifs -o username=xxx,password=xxxx //1.1.1.1/a /win
- Java lang包-Boolean
BrokenDreams
boolean
Boolean类是Java中基本类型boolean的包装类。这个类比较简单,直接看源代码吧。
public final class Boolean implements java.io.Serializable,
- 读《研磨设计模式》-代码笔记-命令模式-Command
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.Collection;
import java.util.List;
/**
* GOF 在《设计模式》一书中阐述命令模式的意图:“将一个请求封装
- matlab下GPU编程笔记
cherishLC
matlab
不多说,直接上代码
gpuDevice % 查看系统中的gpu,,其中的DeviceSupported会给出matlab支持的GPU个数。
g=gpuDevice(1); %会清空 GPU 1中的所有数据,,将GPU1 设为当前GPU
reset(g) %也可以清空GPU中数据。
a=1;
a=gpuArray(a); %将a从CPU移到GPU中
onGP
- SVN安装过程
crabdave
SVN
SVN安装过程
subversion-1.6.12
./configure --prefix=/usr/local/subversion --with-apxs=/usr/local/apache2/bin/apxs --with-apr=/usr/local/apr --with-apr-util=/usr/local/apr --with-openssl=/
- sql 行列转换
daizj
sql行列转换行转列列转行
行转列的思想是通过case when 来实现
列转行的思想是通过union all 来实现
下面具体例子:
假设有张学生成绩表(tb)如下:
Name Subject Result
张三 语文 74
张三 数学 83
张三 物理 93
李四 语文 74
李四 数学 84
李四 物理 94
*/
/*
想变成
姓名 &
- MySQL--主从配置
dcj3sjt126com
mysql
linux下的mysql主从配置: 说明:由于MySQL不同版本之间的(二进制日志)binlog格式可能会不一样,因此最好的搭配组合是Master的MySQL版本和Slave的版本相同或者更低, Master的版本肯定不能高于Slave版本。(版本向下兼容)
mysql1 : 192.168.100.1 //master mysq
- 关于yii 数据库添加新字段之后model类的修改
dcj3sjt126com
Model
rules:
array('新字段','safe','on'=>'search')
1、array('新字段', 'safe')//这个如果是要用户输入的话,要加一下,
2、array('新字段', 'numerical'),//如果是数字的话
3、array('新字段', 'length', 'max'=>100),//如果是文本
1、2、3适当的最少要加一条,新字段才会被
- sublime text3 中文乱码解决
dyy_gusi
Sublime Text
sublime text3中文乱码解决
原因:缺少转换为UTF-8的插件
目的:安装ConvertToUTF8插件包
第一步:安装能自动安装插件的插件,百度“Codecs33”,然后按照步骤可以得到以下一段代码:
import urllib.request,os,hashlib; h = 'eb2297e1a458f27d836c04bb0cbaf282' + 'd0e7a30980927
- 概念了解:CGI,FastCGI,PHP-CGI与PHP-FPM
geeksun
PHP
CGI
CGI全称是“公共网关接口”(Common Gateway Interface),HTTP服务器与你的或其它机器上的程序进行“交谈”的一种工具,其程序须运行在网络服务器上。
CGI可以用任何一种语言编写,只要这种语言具有标准输入、输出和环境变量。如php,perl,tcl等。 FastCGI
FastCGI像是一个常驻(long-live)型的CGI,它可以一直执行着,只要激活后,不
- Git push 报错 "error: failed to push some refs to " 解决
hongtoushizi
git
Git push 报错 "error: failed to push some refs to " .
此问题出现的原因是:由于远程仓库中代码版本与本地不一致冲突导致的。
由于我在第一次git pull --rebase 代码后,准备push的时候,有别人往线上又提交了代码。所以出现此问题。
解决方案:
1: git pull
2:
- 第四章 Lua模块开发
jinnianshilongnian
nginxlua
在实际开发中,不可能把所有代码写到一个大而全的lua文件中,需要进行分模块开发;而且模块化是高性能Lua应用的关键。使用require第一次导入模块后,所有Nginx 进程全局共享模块的数据和代码,每个Worker进程需要时会得到此模块的一个副本(Copy-On-Write),即模块可以认为是每Worker进程共享而不是每Nginx Server共享;另外注意之前我们使用init_by_lua中初
- java.lang.reflect.Proxy
liyonghui160com
1.简介
Proxy 提供用于创建动态代理类和实例的静态方法
(1)动态代理类的属性
代理类是公共的、最终的,而不是抽象的
未指定代理类的非限定名称。但是,以字符串 "$Proxy" 开头的类名空间应该为代理类保留
代理类扩展 java.lang.reflect.Proxy
代理类会按同一顺序准确地实现其创建时指定的接口
- Java中getResourceAsStream的用法
pda158
java
1.Java中的getResourceAsStream有以下几种: 1. Class.getResourceAsStream(String path) : path 不以’/'开头时默认是从此类所在的包下取资源,以’/'开头则是从ClassPath根下获取。其只是通过path构造一个绝对路径,最终还是由ClassLoader获取资源。 2. Class.getClassLoader.get
- spring 包官方下载地址(非maven)
sinnk
spring
SPRING官方网站改版后,建议都是通过 Maven和Gradle下载,对不使用Maven和Gradle开发项目的,下载就非常麻烦,下给出Spring Framework jar官方直接下载路径:
http://repo.springsource.org/libs-release-local/org/springframework/spring/
s
- Oracle学习笔记(7) 开发PLSQL子程序和包
vipbooks
oraclesql编程
哈哈,清明节放假回去了一下,真是太好了,回家的感觉真好啊!现在又开始出差之旅了,又好久没有来了,今天继续Oracle的学习!
这是第七章的学习笔记,学习完第六章的动态SQL之后,开始要学习子程序和包的使用了……,希望大家能多给俺一些支持啊!
编程时使用的工具是PLSQL