R3空间曲线坐标系变换及向量分析
文章目录
- 1. 特殊算式表达
- 1.1爱因斯坦求和约定
- 1.2 Levi-Civita符号(用于叉乘)
- 2. 曲线坐标基向量对应直角坐标的函数表达
- 2.1 柱坐标
- 2.2 球坐标
- 3. 直角与曲线坐标系下的线元,面元,体元基本表达
- 3.1 直角坐标系
- 3.1.1 线元和弧长
- 3.1.2 面元
- 3.1.3体元
- 4. 直角坐标系到曲线坐标系的变换
- 4.1 通用变换方法
- 4.2 柱坐标各方向变换系数
- 4.3 球坐标各方向变换系数
- 5. 总结——曲线坐标系下的线元,面元,体元表达形式
- 5.1 柱坐标
- 5.2 球坐标
- 6. 曲线坐标系下梯度,散度,旋度的表达
- 6.1 梯度表示
- 6.2 散度
- 6.3 旋度表示
数学物理方法的前几节课讲了怎么在 R 3 R^3 R3空间中进行向量分析,其中涉及到了很多与微积分有关的知识,所以特意写这一篇。
1. 特殊算式表达
数学物理方法这几节课给我印象最深的就是它简化了点乘和叉乘运算的表达形式,主要有以下两种简化方法:爱因斯坦求和约定和Levi-Civita符号。
1.1爱因斯坦求和约定
爱因斯坦求和约定可以将向量的表达形式简化,也可以针对向量点乘,或者说是标量积。
Kronecher delta符号
δ i j = { 0 , i ≠ j 1 , i = j \delta_{ij}=\begin{cases}0,&i\neq j \\1,&i=j\end{cases} δij={0,1,i=ji=j
该符号的定义是因为正交坐标系三个基向量 e 1 , e 2 , e 3 \bold e_1,\bold e_2,\bold e_3 e1,e2,e3中相互垂直的向量标量积为0,相同的基向量的标量积为1。
简化三维向量表达
假设我们有一向量 A = A 1 e 1 + A 2 e 2 + A 3 e 3 \bold A=A_1\bold e_1+A_2\bold e_2+A_3\bold e_3 A=A1e1+A2e2+A3e3,爱因斯坦求和约定可以将向量 A \bold A A表达为 A = A i e i = A 1 e 1 + A 2 e 2 + A 3 e 3 \bold A=A_i\bold e_i=A_1\bold e_1+A_2\bold e_2+A_3\bold e_3 A=Aiei=A1e1+A2e2+A3e3
注意,爱因斯坦求和约定中下标都是一样的,这里都是i。
简化向量标量积
假设我们有两个向量 A = A 1 e 1 + A 2 e 2 + A 3 e 3 \bold A=A_1\bold e_1+A_2\bold e_2+A_3\bold e_3 A=A1e1+A2e2+A3e3, B = B 1 e 1 + B 2 e 2 + B 3 e 3 \bold B=B_1\bold e_1+B_2\bold e_2+B_3\bold e_3 B=B1e1+B2e2+B3e3做标量积。
由以上的向量简化形式,我们可以继续推导: A ⋅ B = A i e i ⋅ B j e j = A i B j e i ⋅ e j = A i B j δ i j = A i B i \bold A\cdot\bold B=A_i\bold e_i\cdot B_j\bold e_j=A_iB_j\bold e_i\cdot\bold e_j=A_iB_j\delta_{ij}=A_iB_i A⋅B=Aiei⋅Bjej=AiBjei⋅ej=AiBjδij=AiBi
这与我们的标量积一般形式: A ⋅ B = A 1 B 1 + A 2 B 2 + A 3 B 3 \bold A\cdot\bold B=A_1B_1+A_2B_2+A_3B_3 A⋅B=A1B1+A2B2+A3B3是相一致的。
1.2 Levi-Civita符号(用于叉乘)
向量的叉乘或向量积可以通过Levi-Civita符号进行简化。
Levi-Civita符号简化三阶行列式
ε i j k = { 1 , Even Permutation of indexes − 1 , Odd Permutation of indexes 0 , 2 of indexes are equal \varepsilon_{ijk}=\begin{cases}1,&\text{Even Permutation of indexes}\\ -1,&\text{Odd Permutation of indexes}\\ 0,& \text{2 of indexes are equal}\end{cases} εijk=⎩⎪⎨⎪⎧1,−1,0,Even Permutation of indexesOdd Permutation of indexes2 of indexes are equal
也就是当下标经过偶数次置换(比如123,231,312)之后, ε i j k = 1 \varepsilon_{ijk}=1 εijk=1;当下标经过奇数次置换之后(比如132, 321, 213)之后, ε i j k = − 1 \varepsilon_{ijk}=-1 εijk=−1。
现有两个向量做向量积,其表达式为:
A × B = ∣ e 1 e 2 e 3 A 1 A 2 A 3 B 1 B 2 B 3 ∣ = e 1 ( A 2 B 3 − A 3 B 2 ) + e 2 ( A 3 B 1 − A 1 B 3 ) + e 3 ( A 1 B 2 − A 2 B 1 ) \bold A\times\bold B=\begin{vmatrix}\bold e_1&\bold e_2&\bold e_3\\ A_1&A_2&A_3 \\ B_1&B_2&B_3\end{vmatrix}=\bold e_1(A_2B_3-A_3B_2)+\bold e_2(A_3B_1-A_1B_3)+\bold e_3(A_1B_2-A_2B_1) A×B=∣∣∣∣∣∣e1A1B1e2A2B2e3A3B3∣∣∣∣∣∣=e1(A2B3−A3B2)+e2(A3B1−A1B3)+e3(A1B2−A2B1)
A × B = ε i j k e i A j B k \bold A\times\bold B=\varepsilon_{ijk}\bold e_i A_jB_k A×B=εijkeiAjBk
以上简化的思路就是先确定基向量的下标( e 1 , e 2 , e 3 \bold e_1,\bold e_2,\bold e_3 e1,e2,e3)。并且因为ijk为哑标,所以ijk的顺序是无所谓的,所以有以下的等式:
ε i j k e i A j B k = ε j i k e j A i B k = ε k j i e k A j B i . . . \varepsilon_{ijk}\bold e_i A_jB_k=\varepsilon_{jik}\bold e_j A_iB_k=\varepsilon_{kji}\bold e_k A_jB_i\ ... εijkeiAjBk=εjikejAiBk=εkjiekAjBi ...
2. 曲线坐标基向量对应直角坐标的函数表达
介绍完了向量乘法的两种表达形式的简化,在正式推导坐标之间的变换之前,我们还需要把球坐标和柱坐标的基向量与直角坐标系下的坐标相对应,也就是找到各组基之间的函数关系。曲线坐标系中基向量常见的表达形式是 u 1 , u 2 , u 3 u_1, u_2, u_3 u1,u2,u3
2.1 柱坐标
表达柱坐标系的三个方向的字母有所不同,本文采用 r , θ , z r,\ \theta,\ z r, θ, z来描述柱坐标。
柱坐标与直角坐标系转换的函数为:
{ x ( r , θ , z ) = r cos θ y ( r , θ , z ) = r sin θ z ( r , θ , z ) = z \begin{cases}x(r,\theta,z)=r\cos\theta\\ y(r,\theta,z)=r\sin\theta\\ z(r,\theta,z)=z\end{cases} ⎩⎪⎨⎪⎧x(r,θ,z)=rcosθy(r,θ,z)=rsinθz(r,θ,z)=z
柱坐标到直角坐标系的逆变换为:
{ r ( x , y , z ) = x 2 + y 2 θ ( x , y , z ) = tan − 1 y x z ( x , y , z ) = z \begin{cases}r(x,y,z)=\sqrt{x^2+y^2}\\ \theta(x,y,z)=\tan^{-1}\frac{y}{x}\\ z(x,y,z)=z\end{cases} ⎩⎪⎨⎪⎧r(x,y,z)=x2+y2θ(x,y,z)=tan−1xyz(x,y,z)=z
2.2 球坐标
表达球坐标的三个方向的字母有所不同,本文采用 ρ , ϕ , θ \rho,\ \phi,\ \theta ρ, ϕ, θ来描述柱坐标。
柱坐标与直角坐标系转换的函数为:
{ x ( ρ , ϕ , θ ) = ρ sin ϕ cos θ y ( ρ , ϕ , θ ) = ρ sin ϕ sin θ z ( ρ , ϕ , θ ) = ρ cos ϕ \begin{cases}x(\rho,\phi, \theta)=\rho\sin\phi\cos\theta\\ y(\rho,\phi, \theta)=\rho\sin\phi\sin\theta\\ z(\rho,\phi, \theta)=\rho\cos\phi\end{cases} ⎩⎪⎨⎪⎧x(ρ,ϕ,θ)=ρsinϕcosθy(ρ,ϕ,θ)=ρsinϕsinθz(ρ,ϕ,θ)=ρcosϕ
球坐标的逆变换就不再赘述。
3. 直角与曲线坐标系下的线元,面元,体元基本表达
3.1 直角坐标系
3.1.1 线元和弧长
线元用 d r 2 dr^2 dr2来表示,线元描述的是两点的线段长度的平方。直角坐标系下的表达形式是:
d r 2 = d r ⋅ d r = d x i d x i = d x 1 2 + d x 2 2 + d x 3 2 dr^2=d\bold r\cdot d\bold r=dx_idx_i=dx^2_1+dx^2_2+dx^2_3 dr2=dr⋅dr=dxidxi=dx12+dx22+dx32
弧长的微分形式为(三个方向分别对应一种微分表达):
{ d s 1 = d x d s 2 = d y d s 3 = d z \begin{cases}ds_1=dx\\ ds_2=dy\\ds_3=dz\end{cases} ⎩⎪⎨⎪⎧ds1=dxds2=dyds3=dz
3.1.2 面元
面元有三种,即分别在三个方向上(x,y,z)进行投影:
{ d σ 12 = d x d y , Projection on x-y plane d σ 23 = d y d z , Projection on y-z plane d σ 13 = d x d z , Projection on x-z plane \begin{cases}d\sigma_{12}=dxdy,&\text{Projection on x-y plane}\\ d\sigma_{23}=dydz,&\text{Projection on y-z plane}\\d\sigma_{13}=dxdz,&\text{Projection on x-z plane}\end{cases} ⎩⎪⎨⎪⎧dσ12=dxdy,dσ23=dydz,dσ13=dxdz,Projection on x-y planeProjection on y-z planeProjection on x-z plane
3.1.3体元
面元有三种,即分别在三个方向上进行投影:
d V = d s 1 d s 2 d s 3 = d x d y d z dV=ds_1ds_2ds_3=dxdydz dV=ds1ds2ds3=dxdydz
4. 直角坐标系到曲线坐标系的变换
本节介绍如何从直角坐标下的三种元变换到曲线坐标,多公式预警!
4.1 通用变换方法
通用的方法是设曲线坐标系的三个方向为 u 1 , u 2 , u 3 u_1,u_2,u_3 u1,u2,u3,直角坐标系的三个坐标重写为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,与xyz一一对应,与 u i u_i ui的对应关系是:
{ x 1 = x 1 ( u 1 , u 2 , u 3 ) x 2 = x 2 ( u 1 , u 2 , u 3 ) x 3 = x 3 ( u 1 , u 2 , u 3 ) \begin{cases}x_1=x^1(u_1,u_2,u_3)\\x_2=x^2(u_1,u_2,u_3)\\x_3=x^3(u_1,u_2,u_3)\end{cases} ⎩⎪⎨⎪⎧x1=x1(u1,u2,u3)x2=x2(u1,u2,u3)x3=x3(u1,u2,u3)
注意这里的上标并不代表次幂,只是一个记号。
线元就变成了:
d r 2 = d x i d x i = d x 1 2 + d x 2 2 + d x 3 2 = ∂ x i ∂ u j d u j ∂ x i ∂ u k d u k dr^2=dx_idx_i=dx^2_1+dx^2_2+dx^2_3=\frac{\partial x^i}{\partial u_j}du_j\frac{\partial x^i}{\partial u_k}du_k dr2=dxidxi=dx12+dx22+dx32=∂uj∂xiduj∂uk∂xiduk
这里的 d x i = ∂ x i ∂ u 1 d u 1 + ∂ x i ∂ u 2 d u 2 + ∂ x i ∂ u 3 d u 3 dx_i=\frac{\partial x^i}{\partial u_1}du_1+\frac{\partial x^i}{\partial u_2}du_2+\frac{\partial x^i}{\partial u_3}du_3 dxi=∂u1∂xidu1+∂u2∂xidu2+∂u3∂xidu3
上面的表达式包含爱因斯坦求和,其步骤是先把i确定下来(从1到3),再对jk求和。
令 g i j = ∂ x i ∂ u j ∂ x i ∂ u k g_{ij}=\frac{\partial x^i}{\partial u_j}\frac{\partial x^i}{\partial u_k} gij=∂uj∂xi∂uk∂xi
也就得到: d r 2 = g i j d u i d u j dr^2=g_{ij}du_idu_j dr2=gijduiduj
又因为正交曲线坐标系中的 g i j = { g i i i = j 0 i ≠ j g_{ij}=\begin{cases}g_{ii}&i=j\\0&i\neq j\end{cases} gij={gii0i=ji=j,这样就可以得到曲线坐标系下线元的形式: d r 2 = g 11 ( d u 1 ) 2 + g 22 ( d u 2 ) 2 + g 33 ( d u 3 ) 2 dr^2=g_{11}(du_1)^2+g_{22}(du_2)^2+g_{33}(du_3)^2 dr2=g11(du1)2+g22(du2)2+g33(du3)2
则每一个弧长微分为:
{ d s 1 = g 11 d u 1 = h 1 d u 1 d s 2 = g 22 d u 2 = h 2 d u 2 d s 3 = g 33 d u 3 = h 3 d u 3 \begin{cases}ds_1=\sqrt{g_{11}}du_1=h_1du_1\\ ds_2=\sqrt{g_{22}}du_2=h_2du_2\\ ds_3=\sqrt{g_{33}}du_3=h_3du_3\end{cases} ⎩⎪⎨⎪⎧ds1=g11du1=h1du1ds2=g22du2=h2du2ds3=g33du3=h3du3
下一步就是针对具体的某个曲线坐标系求它对应的变换系数h就可以了。
面元为:
{ d σ 12 = h 1 h 2 d u 1 d u 2 d σ 23 = h 2 h 3 d u 2 d u 3 d σ 13 = h 1 h 3 d u 1 d u 3 , \begin{cases}d\sigma_{12}=h_1h_2du_1du_2\\ d\sigma_{23}=h_2h_3du_2du_3\\d\sigma_{13}=h_1h_3du_1du_3,\end{cases} ⎩⎪⎨⎪⎧dσ12=h1h2du1du2dσ23=h2h3du2du3dσ13=h1h3du1du3,
体元为:
d V = d s 1 d s 2 d s 3 = h 1 h 2 h 3 d u 1 d u 2 d u 3 dV=ds_1ds_2ds_3=h_1h_2h_3du_1du_2du_3 dV=ds1ds2ds3=h1h2h3du1du2du3
4.2 柱坐标各方向变换系数
本章第二节已经说明了直角坐标和柱坐标的转换函数了。
按4.1的公式: d r 2 = d r ⋅ d r = ∂ x i ∂ u j d u j ∂ x i ∂ u k d u k dr^2=d\bold r\cdot d\bold r=\frac{\partial x^i}{\partial u_j}du_j\frac{\partial x^i}{\partial u_k}du_k dr2=dr⋅dr=∂uj∂xiduj∂uk∂xiduk,我们就可以得到:(本质上用的是多变量的链式法则)
d r 2 = ( ∂ x ∂ r d r + ∂ x ∂ θ d θ ) 2 + ( ∂ y ∂ r d r + ∂ y ∂ θ d θ ) 2 + ( ∂ z ∂ z d z ) 2 (1) dr^2=(\frac{\partial x}{\partial r}dr+\frac{\partial x}{\partial \theta}d\theta)^2+(\frac{\partial y}{\partial r}dr+\frac{\partial y}{\partial \theta}d\theta)^2+(\frac{\partial z}{\partial z}dz)^2\tag{1} dr2=(∂r∂xdr+∂θ∂xdθ)2+(∂r∂ydr+∂θ∂ydθ)2+(∂z∂zdz)2(1)
∂ x ∂ r = cos θ ; ∂ x ∂ θ = − r sin θ ; ∂ y ∂ r = sin θ ; ∂ y ∂ θ = r cos θ (2) \frac{\partial x}{\partial r}=\cos\theta;\frac{\partial x}{\partial \theta}=-r\sin\theta;\frac{\partial y}{\partial r}=\sin\theta;\frac{\partial y}{\partial \theta}=r\cos\theta\tag{2} ∂r∂x=cosθ;∂θ∂x=−rsinθ;∂r∂y=sinθ;∂θ∂y=rcosθ(2)
展开公式1并把公式2带入公式1,可以得到:
{ g r r = 1 g θ θ = r 2 g z z = 1 , { h r = 1 h θ = r h z = 1 \begin{cases}g_{rr}=1\\ g_{\theta\theta}=r^2\\ g_{zz}=1\end{cases},\ \begin{cases}h_{r}=1\\ h_{\theta}=r\\ h_{z}=1\end{cases} ⎩⎪⎨⎪⎧grr=1gθθ=r2gzz=1, ⎩⎪⎨⎪⎧hr=1hθ=rhz=1
4.3 球坐标各方向变换系数
最后是直角坐标和球坐标的转换了。
按4.1的公式: d r 2 = d r ⋅ d r = ∂ x i ∂ u j d u j ∂ x i ∂ u k d u k dr^2=d\bold r\cdot d\bold r=\frac{\partial x^i}{\partial u_j}du_j\frac{\partial x^i}{\partial u_k}du_k dr2=dr⋅dr=∂uj∂xiduj∂uk∂xiduk,我们就可以得到:
d r 2 = ( ∂ x ∂ ρ d ρ + ∂ x ∂ ϕ d ϕ + ∂ x ∂ θ d θ ) 2 + ( ∂ y ∂ ρ d ρ + ∂ y ∂ ϕ d ϕ + ∂ y ∂ θ d θ ) 2 + ( ∂ z ∂ ρ d ρ + ∂ z ∂ ϕ d ϕ ) 2 (3) dr^2=(\frac{\partial x}{\partial \rho}d\rho+\frac{\partial x}{\partial \phi}d\phi+\frac{\partial x}{\partial \theta}d\theta)^2+(\frac{\partial y}{\partial \rho}d\rho+\frac{\partial y}{\partial \phi}d\phi+\frac{\partial y}{\partial \theta}d\theta)^2+(\frac{\partial z}{\partial \rho}d\rho+\frac{\partial z}{\partial \phi}d\phi)^2\ \tag{3} dr2=(∂ρ∂xdρ+∂ϕ∂xdϕ+∂θ∂xdθ)2+(∂ρ∂ydρ+∂ϕ∂ydϕ+∂θ∂ydθ)2+(∂ρ∂zdρ+∂ϕ∂zdϕ)2 (3)
∂ x ∂ ρ = sin ϕ cos θ ; ∂ x ∂ ϕ = − ρ cos ϕ cos θ ; ∂ x ∂ θ = − ρ sin ϕ sin θ ; \frac{\partial x}{\partial \rho}=\sin\phi\cos\theta;\frac{\partial x}{\partial \phi}=-\rho\cos\phi\cos\theta;\frac{\partial x}{\partial \theta}=-\rho\sin\phi\sin\theta; ∂ρ∂x=sinϕcosθ;∂ϕ∂x=−ρcosϕcosθ;∂θ∂x=−ρsinϕsinθ; ∂ y ∂ ρ = sin ϕ sin θ ; ∂ y ∂ ϕ = ρ cos ϕ sin θ ; ∂ y ∂ θ = ρ sin ϕ cos θ \frac{\partial y}{\partial \rho}=\sin\phi\sin\theta;\frac{\partial y}{\partial \phi}=\rho\cos\phi\sin\theta;\frac{\partial y}{\partial \theta}=\rho\sin\phi\cos\theta ∂ρ∂y=sinϕsinθ;∂ϕ∂y=ρcosϕsinθ;∂θ∂y=ρsinϕcosθ ∂ z ∂ ρ = cos ϕ ; ∂ z ∂ ϕ = − ρ sin ϕ (4) \frac{\partial z}{\partial \rho}=\cos\phi;\frac{\partial z}{\partial \phi}=-\rho\sin\phi\tag{4} ∂ρ∂z=cosϕ;∂ϕ∂z=−ρsinϕ(4)
展开公式3并把公式4带入公式3,可以得到:
{ h ρ = 1 h ϕ = ρ h θ = ρ sin ϕ \begin{cases}h_{\rho}=1\\ h_{\phi}=\rho\\ h_{\theta}=\rho\sin\phi\end{cases} ⎩⎪⎨⎪⎧hρ=1hϕ=ρhθ=ρsinϕ
5. 总结——曲线坐标系下的线元,面元,体元表达形式
5.1 柱坐标
线元
{ d s r = d r d s θ = r d θ d s z = d z \begin{cases}ds_r=dr\\ds_\theta=rd\theta\\ ds_z=dz\end{cases} ⎩⎪⎨⎪⎧dsr=drdsθ=rdθdsz=dz
面元
{ d σ r θ = d s r d s θ = r d r d θ d σ θ z = d s θ d s z = r d θ d z d σ r z = d s r d s z = d r d z \begin{cases}d\sigma_{r\theta}=ds_rds_\theta =rdrd\theta\\d\sigma_{\theta z}=ds_\theta ds_z =rd\theta dz\\ d\sigma_{rz}=ds_rds_z=drdz\end{cases} ⎩⎪⎨⎪⎧dσrθ=dsrdsθ=rdrdθdσθz=dsθdsz=rdθdzdσrz=dsrdsz=drdz
体元
d V = d s r d s θ d s z = r d r d θ d z dV=ds_rds_\theta ds_z=rdrd\theta dz dV=dsrdsθdsz=rdrdθdz
5.2 球坐标
线元
{ d s ρ = d ρ d s ϕ = ρ d ϕ d s θ = ρ sin θ d θ \begin{cases}ds_\rho=d\rho\\ ds_\phi=\rho d\phi\\ ds_\theta=\rho\sin\theta d\theta \end{cases} ⎩⎪⎨⎪⎧dsρ=dρdsϕ=ρdϕdsθ=ρsinθdθ
面元
{ d σ ρ ϕ = d s ρ d s ϕ = ρ d ρ d ϕ d σ ϕ θ = ρ 2 sin θ d ϕ d θ d σ ρ θ = ρ sin θ d ρ d θ \begin{cases}d\sigma_{\rho\phi}=ds_\rho ds_\phi =\rho d\rho d\phi\\ d\sigma_{\phi\theta}=\rho^2\sin\theta d\phi d\theta \\ d\sigma_{\rho\theta}=\rho\sin\theta d\rho d\theta\end{cases} ⎩⎪⎨⎪⎧dσρϕ=dsρdsϕ=ρdρdϕdσϕθ=ρ2sinθdϕdθdσρθ=ρsinθdρdθ
体元
d V = d s ρ d s ϕ d s θ = ρ 2 sin ϕ d ρ d ϕ d θ dV=ds_\rho ds_\phi ds_\theta=\rho^2\sin\phi d \rho d \phi d\theta dV=dsρdsϕdsθ=ρ2sinϕdρdϕdθ
6. 曲线坐标系下梯度,散度,旋度的表达
以上是曲线坐标系中最基本的几个表达式。本节在上文内容的基础上引出柱坐标和球坐标以及曲线坐标系下梯度,散度,旋度的表达形式。
6.1 梯度表示
直角坐标系中某一标量场 f ( x , y , z ) f(x,y,z) f(x,y,z)的梯度表达是为 ∇ f = ∂ f ∂ x e i + ∂ f ∂ y e j + ∂ f ∂ z e k \nabla f=\frac{\partial f}{\partial x}\bold e_i+\frac{\partial f}{\partial y}\bold e_j+\frac{\partial f}{\partial z}\bold e_k ∇f=∂x∂fei+∂y∂fej+∂z∂fek,梯度有一个性质是: ∇ f ⋅ d r = d f \nabla f\cdot d\bold r=df ∇f⋅dr=df
如果是任意正交曲线坐标系下的标量场 f ( u 1 , u 2 , u 3 ) f(u_1,u_2,u_3) f(u1,u2,u3)的话,它的微分形式本身可以表达为 d f = ∂ f ∂ u i e u i df=\frac{\partial f}{\partial u_i}\bold e_{u_i} df=∂ui∂feui,另外一种与梯度相关的微分表达等式是:
d f = ∇ f i d s i = ∇ f i h i d u i df=\nabla f_i ds_i =\nabla f_i h_idu_i df=∇fidsi=∇fihidui
∂ f ∂ u i = ∇ f i h i d u i → ∇ f i = 1 h i ∂ f ∂ u i \frac{\partial f}{\partial u_i}=\nabla f_i h_idu_i\ \to \ \nabla f_i=\frac{1}{h_i}\frac{\partial f}{\partial u_i} ∂ui∂f=∇fihidui → ∇fi=hi1∂ui∂f
完整的梯度表达形式就是:
∇ f = 1 h 1 ∂ f ∂ u 1 e u 1 + 1 h 2 ∂ f ∂ u 2 e u 2 + 1 h 3 ∂ f ∂ u 3 e u 3 \nabla f=\frac{1}{h_1}\frac{\partial f}{\partial u_1}\bold e_{u_1}+\frac{1}{h_2}\frac{\partial f}{\partial u_2}\bold e_{u_2}+\frac{1}{h_3}\frac{\partial f}{\partial u_3}\bold e_{u_3} ∇f=h11∂u1∂feu1+h21∂u2∂feu2+h31∂u3∂feu3
曲线坐标系下的哈密顿算子 ∇ \nabla ∇的表达形式为:
∇ = 1 h 1 ∂ ∂ u 1 e u 1 + 1 h 2 ∂ ∂ u 2 e u 2 + 1 h 3 ∂ ∂ u 3 e u 3 \nabla =\frac{1}{h_1}\frac{\partial }{\partial u_1}\bold e_{u_1}+\frac{1}{h_2}\frac{\partial }{\partial u_2}\bold e_{u_2}+\frac{1}{h_3}\frac{\partial }{\partial u_3}\bold e_{u_3} ∇=h11∂u1∂eu1+h21∂u2∂eu2+h31∂u3∂eu3
6.2 散度
假设曲线坐标系下有一向量场 A \bold A A,其散度的定义为:
div A = lim Δ V → 0 1 Δ V ∯ S A ⋅ d σ \text{div}\bold A=\lim_{\Delta V\to 0}\frac{1}{\Delta V}\oiint_S\bold A\cdot d \bold\sigma divA=ΔV→0limΔV1∬SA⋅dσ
如下图,随意选取一个基向量的方向,比如说是 e 1 \bold e_1 e1,表达出通过平面ABCD和A’B’C’D’的通量差即可。
通量差为:
∂ ∂ u 1 ( A 1 h 2 h 3 ) d u 1 d u 2 d u 3 \frac{\partial }{\partial u_1}(A_1h_2h_3)du_1du_2du_3 ∂u1∂(A1h2h3)du1du2du3
之后除以体积元 d V = h 1 h 2 h 3 u 1 u 2 u 3 dV=h_1h_2h_3u_1u_2u_3 dV=h1h2h3u1u2u3即可得到 e 1 \bold e_1 e1方向的散度表达式: 1 h 1 h 2 h 3 ∂ ∂ u 1 ( A 1 h 2 h 3 ) \frac{1}{h_1h_2h_3}\frac{\partial }{\partial u_1}(A_1h_2h_3) h1h2h31∂u1∂(A1h2h3)
整体的散度表达式为:
∇ ⋅ A = 1 h 1 h 2 h 3 [ ∂ ∂ u 1 ( A 1 h 2 h 3 ) + ∂ ∂ u 2 ( A 2 h 3 h 1 ) + ∂ ∂ u 3 ( A 3 h 1 h 2 ) ] \nabla\cdot\bold A= \frac{1}{h_1h_2h_3}\begin{bmatrix}\frac{\partial }{\partial u_1}(A_1h_2h_3)+\frac{\partial }{\partial u_2}(A_2h_3h_1)+\frac{\partial }{\partial u_3}(A_3h_1h_2)\end{bmatrix} ∇⋅A=h1h2h31[∂u1∂(A1h2h3)+∂u2∂(A2h3h1)+∂u3∂(A3h1h2)]
当 h 1 = h 2 = h 3 = 1 h_1=h_2=h_3=1 h1=h2=h3=1的时候,上述表达式与直角坐标系的散度表达式相同。
6.3 旋度表示
旋度的定义
与散度的定义类似,旋度的定义也是通过极限来定义的。假设空间中有一向量场 A \bold A A,其旋度为:
curl A ≡ ∇ × A = lim Δ σ → 0 1 Δ σ ∮ C A ⋅ d l \text{curl}\bold A\equiv\nabla\times\bold A=\lim_{\Delta \sigma\to 0}\frac{1}{\Delta\sigma}\oint_C \bold A\cdot d\bold l curlA≡∇×A=Δσ→0limΔσ1∮CA⋅dl
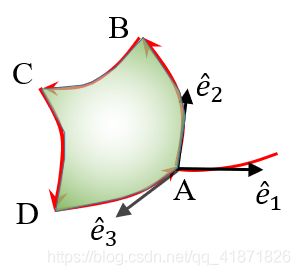
推导思路:
如上图,由于是曲线包围的是曲面,所以先计算一个方向上通过这一闭合曲线ABCD的线积分,除以该方向的面元就可以得到该方向的旋度分量,之后再考虑其他剩余方向。
可以参考下图:

任意正交曲线坐标系下的旋度公式:(行列式形式)
∇ × A = 1 h 1 h 2 h 3 ∣ e u 1 h 1 e u 1 h 2 e u 1 h 3 ∂ ∂ u 1 ∂ ∂ u 2 ∂ ∂ u 3 h 1 A 1 h 2 A 2 h 3 A 3 ∣ \nabla\times\bold A=\frac{1}{h_1h_2h_3}\begin{vmatrix}\bold e_{u_1}h_1&\bold e_{u_1}h_2&\bold e_{u_1}h_3\\ \\ \frac{\partial}{\partial u_1}&\frac{\partial}{\partial u_2}&\frac{\partial}{\partial u_3}\\ \\ h_1A_1&h_2A_2&h_3A_3 \end{vmatrix} ∇×A=h1h2h31∣∣∣∣∣∣∣∣∣∣eu1h1∂u1∂h1A1eu1h2∂u2∂h2A2eu1h3∂u3∂h3A3∣∣∣∣∣∣∣∣∣∣
球坐标和柱坐标下的散度和旋度表达式只需带入相应的参数 h h h即可。
