R语言与属性数据分析

1. 属性数据的描述性分析

1）属性数据形式的转化

* 将数据框中的分类数据（统计好的）转换成频数表
	# input data
	Reason<-c("操作","设备","工具","工艺","材料")
	Count<-c(22,526,292,89,47)
	data0<-data.frame(Reason,Count);data0
	# change to the table
	ftable<-table(rep(Reason,Count));data1
	names(Count)<-Reason;Count

* 将数据框中的分类数据（未统计好的）转换成频数表
	ftable<-table(data$classvar);ftable

* 频数表转换成频率表
	ftable/sum(ftable)
	prop.table(ftable)

* 列联表和概率列联表
	ctable<-table(data);ctable
	prop.table(ctable)

* 将频率表转化为数据集
	Indicator<-c(1:5) // c('A','B','C')
	data<-rep(Indicator,ftable);data

2）属性数据的描述性统计图

	barplot(Count,main='条形图')
	pie(Count,radius = 1,main='饼图')
	library(qcc)
	pareto.chart(Count, ylab = "频数",ylab2 = "累计百分比(%)",main='帕累托图')

3）属性数据的基本统计量

* 描述中心位置的统计量
	median()
	quantile( , probs = c(0.25,0.75))
	getmode()
	# the mode function
	getmode<-function(x){
	  tab<-table(x)
	  tab.max<-max(tab)
	  if (all(tab == tab.max)) {mod<-NA}
	  else if(is.numeric(x)) {mod<-as.numeric(names(tab)[tab == tab.max])}
	  else {mod<-names(tab)[tab == tab.max]}
	  names(mod)<-'mode'
	  return(mod)
	}

* 描述离散程度的统计量(离异比率、GS指数、熵)
	var.ratio<-function(x){
	  tab<-table(x)
	  mod<-getmode(x)
	  ratio=1-tab[names(tab)==mod]/sum(tab)
	  names(ratio)<-'variation ratio'
	  return(ratio)
	}
	GS.index<-function(x){
	  tab<-table(x)
	  p<-prop.table(tab)
	  index<-1-sum(p^2)
	  names(index)<-'GS index'
	  return(index)
	}
	entropy<-function(x){
	  #x is the raw data
	  tab<-table(x)
	  p<-prop.table(tab)
	  entropy<- (-1)*sum(p*log(p))
	  names(entropy)<-'entropy'
	  return(entropy)
	}

2. 单一属性分类数据

1）分类数据的概率检验

* 不含参数的Chi2检验
	chisq.test(table, correct = TURE/FALSE, p = p0, rescale.p = TRUE/FALSE)
* 不含参数的LRT检验
	library(RVAideMemoire)
	G.test(table,p=p0)
# 等概率检验时，p0 = rep(1/length(x2), length(x2))
---------------------------------------------------------------

* 参数的极大似然估计(MLE) (用数值方法解)
* 含一个参数
	fn_likelihood<-function(p){
	  ... #log-likelihood function
	}
	result<-optimize(f=fn_likelihood, interval=c(0,1), maximum = TRUE);result
	# optimize函数得到maximum和objective两个值
	p_hat<-result$maximum  # the MLE for p
	p<-c(...)
	
* 含多个参数
	fn_likelihood<-function(x){
	  p<-x[1]
	  q<-x[2]
	  ... #log-likelihood function
	}
	result<-optim(par = c(0.1,0.1),fn_likelihood,control = list(fnscale = -1));result
	p_hat<-result$par[1]  # the MLE for p
	q_hat<-result$par[2]  # the MLE for q
---------------------------------------------------------------

* 含参数的Chi2检验
	Chistat<-chisq.test(x, correct = FALSE, p = p, rescale.p = FALSE)$statistic
* 含参数的LRT检验
	LRTstat<-G.test(x,p = p)$statistic
---------------------------------------------------------------

* 统计决策
	# critical value
	qchisq(p=0.95, df=r-m-1,lower.tail = TRUE)
	# p value
	pchisq(Chistat,df=r-m-1,lower.tail = FALSE)
	pchisq(LRTstat,df=r-m-1,lower.tail = FALSE)

3. 四格表

1）四格表的独立性检验

* U检验（单边）
	U.stat=sqrt(n)*(n11*n22-n12*n21)/sqrt(n1_*n2_*n_1*n_2) #未修正
	U.stat=sqrt(n)*(n11*n22-n12*n21 ± n/2)/sqrt(n1_*n2_*n_1*n_2) #修正
	pvalue=pnorm(U.stat, mean = 0, sd = 1, lower.tail = FALSE)
* Chi2检验（双边）
	Chi.stat=n*(n11*n22-n12*n21)^2/(n1_*n2_*n_1*n_2) #未修正
	Chi.stat=n*(abs(n11*n22-n12*n21)-n/2)^2/(n1_*n2_*n_1*n_2) #修正
	pvalue=pchisq(Chi.stat, df=1, ncp=0, lower.tail = FALSE)
* LRT检验
	LRT.stat1=-2*(n11*log(n1_*n_1/n11/n)+n12*log(n1_*n_2/n12/n)+n21*log(n2_*n_1/n21/n)+n22*log(n2_*n_2/n22/n))
	pvalue=pchisq(LRT.stat, df=1, ncp=0, lower.tail = FALSE)

* Fisher精确检验
	table<-matrix(c(n11,n12,n21,n22),byrow=TRUE,nrow=2,ncol=2)
	fisher.test(x=table,alternative = "greater"/"less"/"two.sided")
* U近似精确检验
	U.stat=sqrt(n-1)*(n11*n22-n12*n21)/sqrt(n1_*n2_*n_1*n_2) #未修正
	U.stat=sqrt(n)*(n11*n22-n12*n21 ± n/2)/sqrt(n1_*n2_*n_1*n_2) #修正
* Mantel Haenszel Chi2近似精确检验
	Chi.stat=(n-1)*(n11*n22-n12*n21)^2/(n1_*n2_*n_1*n_2) #未修正
	Chi.stat=(n-1)*(abs(n11*n22-n12*n21)-n/2)^2/(n1_*n2_*n_1*n_2) #修正

* OR优比检验
	U.stat <-log(n11*n22/(n12*n21))/sqrt(1/n11+1/n12+1/n21+1/n22)
	Chi.stat <- log(n11*n22/(n12*n21))^2/(1/n11+1/n12+1/n21+1/n22)

2）四格表的边缘齐性（对称性）检验

* McNemar Chi2检验
	Chi.stat=(n12-n21)^2/(n12+n21)
* LRT检验
	LRT.stat=-2*(n12*log((n12+n21)/2/n12)+n21*log((n12+n21)/2/n21))

chisq.test 和 G.test 函数不适用于四格表的分析，但可以用在分类数据和列联表的检验中;
可用于四格表检验的自带函数只有fisher.test

4. 二维列联表

1）二维列联表的独立性检验

	table<-matrix(c(...),byrow=TRUE,nrow=r,ncol=c)
	chisq.test(table, correct = TURE/FALSE)
	library(RVAideMemoire)
	G.test(table)

2）二维列联表的相合性度量和检验

一定是单边检验

# Calculate Kendall_tau, gamma and Somers d
	# x is a table(matrix)
	assocoef<-function(x){
	  Gcount<-function(x){#this function is used to calculate G
	    r<-dim(x)[1];c<-dim(x)[2];G<-0
	    for (i in 1:(r-1)){
	      for (j in 1:(c-1)){
	        G<-G+x[i,j]*sum(x[(i+1):r,(j+1):c])
	      }
	    }
	    return(G)
	  }
	  Hcount<-function(x){#this function is used to calculate H
	    r<-dim(x)[1];c<-dim(x)[2];H<-0
	    for (i in 1:(r-1)){
	      for (j in 2:c){
	        H<-H+x[i,j]*sum(x[(i+1):r,1:(j-1)])
	      }
	    }
	    return(H)
	  }
	  TAcount<-function(x){#this function is used to calculate TA
	    r<-dim(x)[1];TA<-0
	    for (i in 1:r){
	      TA<-TA+sum(x[i,])*(sum(x[i,])-1)/2
	    }
	    return(TA)
	  }
	  TBcount<-function(x){#this function is used to calculate TB
	    c<-dim(x)[2];TB<-0
	    for (j in 1:c){
	      TB<-TB+sum(x[,j])*(sum(x[,j])-1)/2
	    }
	    return(TB)
	  }
	  G<-Gcount(x);H<-Hcount(x);TA<-TAcount(x);TB<-TBcount(x);n<-sum(x)
	  tau<-(G-H)/sqrt((n*(n-1)/2-TA)*(n*(n-1)/2-TB))
	  gamma<-(G-H)/(G+H)
	  dCR<-(G-H)/(n*(n-1)/2-TA)
	  dRC<-(G-H)/(n*(n-1)/2-TB)
	  return(list(G=G,H=H,tau=tau,gamma=gamma,dCR=dCR,dRC=dRC))
	}
assocoef(table)
tau
gamma
dCR
dRC

# Association test statistic based on z=G-H （use the approximate variance for z）
	assotest<-function(x){
	  G<-assocoef(x)$G; H<-assocoef(x)$H;n<-sum(x);z<-G-H
	  z.var<-(n^3-sum((rowSums(x))^3))*(n^3-sum((colSums(x))^3))/9/n^3
	  U<-z/sqrt(z.var)
	  chisqstat<-U^2
	  return(list(U=U,chisqstat=chisqstat,z=z,z.var=z.var))
	}
assotest(table)

3）方表的一致性度量和检验

单边检验

# kappa and agreement test statistic	
	kappatest<-function(x){
	  n<-sum(x)
	  q1<-sum(diag(x))/n
	  q2<-sum(rowSums(x)*colSums(x))/n^2
	  kappa<-(q1-q2)/(1-q2)
	  var.kappa<-(q2+q2^2-sum(rowSums(x)*colSums(x)*(rowSums(x)+colSums(x)))/n^3)/(n-1)/(1-q2)^2
	  U<-kappa/sqrt(var.kappa)
	  return(list(kappa=kappa,var.kappa=var.kappa,U=U))
	}

kappatest(table)

5. 三维列联表

1）三维列联表的独立性检验

• indtset3d 函数定义
  • type = mutual.ind：完全独立性检验
  • type = joint.ind.A | B | C：分块独立性检验
  • type = cond.ind.A | B | C：条件独立性检验

indtest3d<-function(x,type="mutual.ind"){
  #this function is for independence test for 3-dimension r*c*t contingency table
  #x is an array including frequencies of r*c*t contingency table for row A,column B,stratum C.
  #output includes Pearson chi-square test and likelihood ratio test
  r<-dim(x)[1];c<-dim(x)[2];t<-dim(x)[3];n<-sum(x)
  m<-array(0,dim=c(r,c,t))
  Pearson.chisq<-likelihood.ratio.base<-0
  if (type=="mutual.ind"){#for mutual independence (A,B,C)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[i,,])*sum(x[,j,])*sum(x[,,k])/n^2
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-r*c*t-r-c-t+2
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  }
  if (type=="joint.ind.A"){#for joint independence (A,BC)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[i,,])*sum(x[,j,k])/n
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-(r-1)*(c*t-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  if (type=="joint.ind.B"){#for joint independence (B,AC)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[,j,])*sum(x[i,,k])/n
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-(c-1)*(r*t-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  if (type=="joint.ind.C"){#for joint independence (C,AB)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[,,k])*sum(x[i,j,])/n
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-(t-1)*(r*c-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  if (type=="cond.ind.A"){#for conditional independence (AB,AC)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[i,j,])*sum(x[i,,k])/sum(x[i,,])
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-r*(c-1)*(t-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  if (type=="cond.ind.B"){#for conditional independence (BA,BC)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[i,j,])*sum(x[,j,k])/sum(x[,j,])
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-c*(r-1)*(t-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  if (type=="cond.ind.C"){#for conditional independence (CA,CB)
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m[i,j,k]<-sum(x[i,,k])*sum(x[,j,k])/sum(x[,,k])
          Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
          likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
        }
      }
    }
    df<-t*(r-1)*(c-1)
    p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
    likelihood.ratio<- (-2)*likelihood.ratio.base
    p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)
  } 
  return(list(Pearson.chisq=Pearson.chisq,likelihood.ratio=likelihood.ratio,
              df=df,p.Pearson=p.Pearson,p.likelihood=p.likelihood))
}

2）三维列联表的相合性检验

对 r x 2 x 2的三维列联表：

• Cochran-Mantel Haenszel 检验（条件相合性检验）
  先做分层相合性检验（四格表的Mantel Haenszel Chi2检验），再做条件相合检验
• Breslow-Day 检验（检验分层后各层四格表的相合程度是否相同）

BreslowDaytest<-function(x){
  #x is an array including frequencies of r*2*2 contingency table for row A,column B,stratum C.
  r<-dim(x)[1]
  theta<-NULL;a<-NULL
  for (i in 1:r){
    theta[i]<-x[i,1,1]*x[i,2,2]/x[i,1,2]/x[i,2,1]
    a[i]<-1/x[i,1,1]+1/x[i,1,2]+1/x[i,2,1]+1/x[i,2,2]
  }
  eta<-log(theta)
  etabar<-sum(eta/a)/sum(1/a)
  chisq.stat<-sum((eta-etabar)^2/a)
  df=r-1
  p.chisq<-pchisq(chisq.stat,df=df,lower.tail = FALSE)
  return(list(chisq.stat=chisq.stat,df=df,p.chisq=p.chisq))
}

3）三维列联表的相关性检验

• 饱和模型（三个属性全部相关，两两之间、三者之间都有交互作用）
• 两两相关模型 / 齐次相关模型
  所有独立性模型都被拒绝后，可以考虑两两相关模型

homogetest<-function(x){
  #this function is to test homogeneous association model (AB,AC,BC) 
  #x is an array including frequencies of r*c*t contingency table for row A,column B,stratum C.
  #output includes expected frequencies, Pearson chi-square test and likelihood ratio test
  r<-dim(x)[1];c<-dim(x)[2];t<-dim(x)[3]
  m0<-m1<-array(1,dim=c(r,c,t)) #initial value
  m2<-m3<-array(0,dim=c(r,c,t))
  
  b<-0 #denote number of replications
  while (mean(abs(m3-m0))>=10^(-6)){#begin replication
    m0<-m1 #update initial value
    for (k in 1:t){
      for (i in 1:r){
        for (j in 1:c){
          m1[i,j,k]<- m0[i,j,k]/sum(m0[i,j,])*sum(x[i,j,])
        }
      }
    }
    for (j in 1:c){
      for (i in 1:r){
        for (k in 1:t){
          m2[i,j,k]<- m1[i,j,k]/sum(m1[i,,k])*sum(x[i,,k])
        }
      }
    }
    for (i in 1:r){
      for (j in 1:c){
        for (k in 1:t){
          m3[i,j,k]<- m2[i,j,k]/sum(m2[,j,k])*sum(x[,j,k])
        }
      }
    }
    b<-b+1
    m1<-m3
  }
  m<-m3 #expected frequencies for homogeneous association model (AB,AC,BC) 
  Pearson.chisq<-likelihood.ratio.base<-0
  for (i in 1:r){
    for (j in 1:c){
      for (k in 1:t){
        Pearson.chisq<-Pearson.chisq+(x[i,j,k]-m[i,j,k])^2/m[i,j,k]
        likelihood.ratio.base<- likelihood.ratio.base+x[i,j,k]*log(m[i,j,k]/x[i,j,k])
      }
    }
  }
  df<-(r-1)*(c-1)*(t-1)
  p.Pearson<-pchisq(Pearson.chisq,df=df,lower.tail = FALSE)
  likelihood.ratio<- (-2)*likelihood.ratio.base
  p.likelihood<-pchisq(likelihood.ratio,df=df,lower.tail = FALSE)

  return(list(m=m,replication.no=b,Pearson.chisq=Pearson.chisq,likelihood.ratio=likelihood.ratio,
              df=df,p.Pearson=p.Pearson,p.likelihood=p.likelihood))
}

6. Logistic回归模型

1）二分类Logistic回归案例

数据读入和预处理

# 读入原始数据
cuse<- read.table("cuse.txt", header=TRUE)
cuse
summary(cuse)

# 读入赋值和重组变换后的数据
cuseraw<- read.table("cuseraw.txt", header=TRUE)
cuseraw
summary(cuseraw)

attach(cuseraw)

# 频数分布表
Onefactor1<- table(rep(noMore,count),rep(using,count));Onefactor1  # noMore & using
Onefactor2<- table(rep(age,count),rep(using,count));Onefactor2     # age & using
twofactor<- table(rep(noMore,count),rep(age,count),rep(using,count));twofactor  # noMore age & using

detach(cuseraw)

# 频数表重组后定义dataframe数据集
cuse.onefactor1<- data.frame(list(wantsMore=c("yes","no"), using=c(219,288),notUsing=c(753,347)));cuse.onefactor1
cuse.onefactor2<- data.frame(list(age=c("<25","25-29","30-39","40-49"),using=c(72,105,237,93),notUsing=c(325,299,375,101)));cuse.onefactor2
cuse.twofactor<- data.frame(list(age=c("<25","<25","25-29","25-29","30-39","30-39","40-49","40-49"),wantsMore=c("yes","no","yes","no","yes","no","yes","no"), 
                                 using=c(58,14,68,37,79,158,14,79),notUsing=c(265,60,215,84,230,145,43,58)));cuse.twofactor

Logistic模型建立和分析

① glm(formula, family=binomial(link=logit), data, weights, subset, …);
② the response can be a matrix where the first column is the number of “successes” and the second column is the number of “failures”;

attach(cuse.onefactor1)

## 零模型
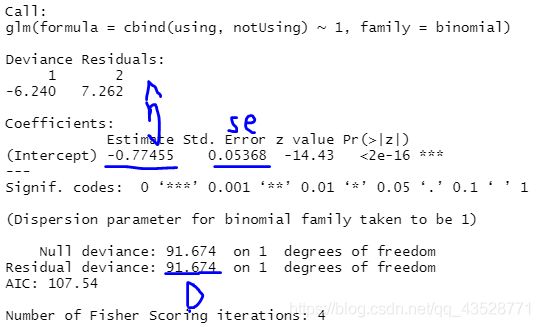
fit.null1<- glm(cbind(using, notUsing) ~ 1, family = binomial)
summary(fit.null1)

## 单因素模型
# R sorts the levels of a factor in alphabetical order, and the first level of a factor is choosen as the reference cell.
noMore <- wantsMore == "no"  # 定义示性变量
fit.desire.no<- glm(cbind(using, notUsing) ~ noMore, family = binomial)
summary(fit.desire.no)

# 单因素模型的方差分析表
anova(fit.null1,fit.desire.no)

detach(cuse.onefactor1)

结果分析

• 拟合优度的检验：D大于临界值 → 拟合模型不充分
  本例中，零模型拟合不充分(D0)，单因素模型拟合充分且就是饱和模型(D1)
• 嵌套模型的检验：D(H0) - D(H1)大于临界值 → H1模型增加的效应显著
  本例中，效应noMore是显著的

零模型	单因素模型