Pytorch学习笔记

此文为学习"莫烦Python"的Pytorch笔记

2.2 Variable变量

神经网络中的参数都是变量的形式,参数的更新是以Variable为基础的;Variable 需要从torch.autograd导入.;误差传播是根据Variable搭建的图来进行计算的,require_grad=True才计算变量节点的梯度.tensor无法反向传播,Variable才可以反向传播.
import torch
from torch.autograd import Variable # torch 中 Variable 模块

# 先生鸡蛋
tensor = torch.FloatTensor([[1,2],[3,4]])
# 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor, requires_grad=True)

print(tensor)
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable)

t_out = torch.mean(tensor*tensor)       # x^2
v_out = torch.mean(variable*variable)   # x^2
print(t_out)
print(v_out)    # 7.5

v_out.backward()    # 模拟 v_out 的误差反向传递

# 下面两步看不懂没关系, 只要知道 Variable 是计算图的一部分, 可以用来传递误差就好.
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2

print(variable.grad)    # 初始 Variable 的梯度
'''
 0.5000  1.0000
 1.5000  2.0000
'''

因为v_out是从variable计算而来,所以通过v_out.backward()进行反向传播的时候也会计算到variable的梯度.
下面是variable包含的其他内容

print(variable)     #  Variable 形式
"""
Variable containing:
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data)    # tensor 形式
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data.numpy())    # numpy 形式
"""
[[ 1.  2.]
 [ 3.  4.]]
"""

什么是激励函数?

通过激励函数可以使一些线性函数可以解决非线性问题
y=Wx -> y=AF(Wx)
其中的AF可以是relu函数,sigmoid函数,tanh函数
当神经网络的体量比较大的时候,激活函数的选取很重要,不合适的选择可能导致梯度爆炸等问题.

• 在少量层的结构中,我们可以尝试很多种的激励函数,在CNN中,推荐的是relu,在RNN中,推荐tanh和relu

3.1 Regression回归

造数据的代码中,使用torch.unsqueeze将一维的数据变成二维的数据,因为torch中只会处理二维数据.

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# # 画图
# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()

x, y = Variable(x),Variable(y)


class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构

• Net的class继承了torch的神经网络模块;每一个神经网络的模块都会包括__init__ 和 forward 两个函数;__init__存储搭建层所需要的信息,forward是神经网络前向传播的过程.
• __init__中需要继承Net的模块, 即super(Net, self).init();self.hiddend定义隐藏层,包含的信息为有多少个输入(n_features),有多少输出(n_hidden);self.predict定义输出层
• forward()中输入x,经过hidden layer之后输出n_hidden个数,然后再用relu激活函数激活(嵌套隐藏层输出的信息),这里的predict层没有使用激励函数是因为通常归回问题的值域范围很灵活,用了激励函数的话会限制输出值的范围
  搭建了神经网络之后,就需要优化训练网络

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

• torch.optim子模块用于训练神经网络,最常用的有SGD(随机梯度下降)优化器来优化神经网络参数;其中需要传入神经网络的参数,即net.parameters,还需要给定学习率lr(一般小于1)
• loss_func是torch中计算误差的函数,这里使用MSELoss(均方差)
• t为训练步数,此处设置为100步;loss_func中的prediction为预测值,y为真实值(位置不能反)
• 接下来三步就是优化神经网络参数:首先使用optimizer.zero_grad()将神经网络参数的梯度全部降为0(因为每次计算梯度以后都会被保留);然后使用loss.backward()进行这一次的反向传递,计算出节点的梯度;optimizer.step()就以0.5的LR优化参数.

3.2 Classification分类

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# make fake data
n_data = torch.ones(100, 2)
x0 = torch.normal(2*n_data, 1)      # class0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100)               # class0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1)     # class1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100)                # class1 y data (tensor), shape=(100, 1)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # shape (200, 2) FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor)    # shape (200,) LongTensor = 64-bit integer

# The code below is deprecated in Pytorch 0.4. Now, autograd directly supports tensors
# x, y = Variable(x), Variable(y)

# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()


class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
        self.out = torch.nn.Linear(n_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.out(x)
        return x

net = Net(n_feature=2, n_hidden=10, n_output=2)     # define the network
print(net)  # net architecture

optimizer = torch.optim.SGD(net.parameters(), lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()  # the target label is NOT an one-hotted

plt.ion()   # something about plotting

for t in range(100):
    out = net(x)                 # input x and predict based on x
    loss = loss_func(out, y)     # must be (1. nn output, 2. target), the target label is NOT one-hotted

    optimizer.zero_grad()   # clear gradients for next train
    loss.backward()         # backpropagation, compute gradients
    optimizer.step()        # apply gradients

    if t % 2 == 0:
        # plot and show learning process
        plt.cla()
        prediction = torch.max(out, 1)[1]
        pred_y = prediction.data.numpy()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()

注意与之前的差别,这里net = Net(n_feature=2, n_hidden=10, n_output=2)是输入两个特征,而之前是输入一个特征.
这里是多分类,所以使用CrossEntropyLoss()
经过net()输出的向量还不是概率值,可以通过**F.softmax()**转化为多分类的概率(相当于再套一层激活函数)

3.3 快速搭建法

import torch
import torch.nn.functional as F


# replace following class code with an easy sequential network
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
        self.predict = torch.nn.Linear(n_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

net1 = Net(1, 10, 1)

# easy and fast way to build your network
net2 = torch.nn.Sequential(
    torch.nn.Linear(1, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 1)
)


print(net1)     # net1 architecture

使用torch.nn.Sequential()可以快速搭建神经网络
如前所加的linear的神经层,可以使用torch.nn.Linear(1,10),指两个输入,隐藏层有十个神经元.
激励函数使用**torch.nn.ReLU()**添加即可

3.4 保存提取

import torch
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# fake data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # noisy y data (tensor), shape=(100, 1)

# The code below is deprecated in Pytorch 0.4. Now, autograd directly supports tensors
# x, y = Variable(x, requires_grad=False), Variable(y, requires_grad=False)


def save():
    # save net1
    net1 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )
    optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)
    loss_func = torch.nn.MSELoss()

    for t in range(100):
        prediction = net1(x)
        loss = loss_func(prediction, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # plot result
    plt.figure(1, figsize=(10, 3))
    plt.subplot(131)
    plt.title('Net1')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

    # 2 ways to save the net
    torch.save(net1, 'net.pkl')  # save entire net
    torch.save(net1.state_dict(), 'net_params.pkl')   # save only the parameters


def restore_net():
    # restore entire net1 to net2
    net2 = torch.load('net.pkl')
    prediction = net2(x)

    # plot result
    plt.subplot(132)
    plt.title('Net2')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)


def restore_params():
    # restore only the parameters in net1 to net3
    net3 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )

    # copy net1's parameters into net3
    net3.load_state_dict(torch.load('net_params.pkl'))
    prediction = net3(x)

    # plot result
    plt.subplot(133)
    plt.title('Net3')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
    plt.show()

# save net1
save()

# restore entire net (may slow)
restore_net()

# restore only the net parameters
restore_params()

在save()函数中,首先搭建神经网络,训练好之后,就可以使用torch.save()保存神经网络,传入的参数是net1时保存的是整个神经网络,传入net1.state_dict()时保存的是模型的参数.此外还需要传入文件名,是".pkl"格式.

**restore_net()**是提取的第一种方法,直接使用torch.load()就可以读入模型.

restore_params()对应于存的是参数的情况,这种方法读模型时需要先按照模型本身的方式建立神经网络,然后使用.load_state_dict()读取之前保存的参数文件.

3.5 批数据处理

神经网络中的训练形式不只是把所有的训练一起完成,当数据量非常大时就可以使用批训练以提高训练速度和效率.

import torch
import torch.utils.data as Data

torch.manual_seed(1)    # reproducible

BATCH_SIZE = 5
# BATCH_SIZE = 8

x = torch.linspace(1, 10, 10)       # this is x data (torch tensor)
y = torch.linspace(10, 1, 10)       # this is y data (torch tensor)

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
    dataset=torch_dataset,      # torch TensorDataset format
    batch_size=BATCH_SIZE,      # mini batch size
    shuffle=True,               # random shuffle for training
    num_workers=2,              # subprocesses for loading data
)


def show_batch():
    for epoch in range(3):   # train entire dataset 3 times
        for step, (batch_x, batch_y) in enumerate(loader):  # for each training step
            # train your data...
            print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
                  batch_x.numpy(), '| batch y: ', batch_y.numpy())


if __name__ == '__main__':
    show_batch()

从torch.utils.data中导入Data模块,
BATCH_SIZE定义每一批抽取的数据量.
Data.TensorDataset()定义一个数据集,传入参数data_tensor和target_tensor分别为数据张量和标签张量
Data.DataLoader()实现训练的分批
epoch指将整体的数据训练的次数.
在每一个epoch中,step表示训练的是第几部分.
当BATCH_SIZE选得比较大时,后面的step可能数据不够,那就会返回剩下的数据.

优化器 Optimizer

随着数据量增大,神经网络变复杂,计算量也会变得非常大.需要一些方法来加速神经网络的训练
最基础的方法是Stochastic Gradient Descent(SGD)
还有很多其它很快的加速方法．

３.６优化器 Optimizer

优化器的作用就是优化神经网络的参数

"""
View more, visit my tutorial page: https://morvanzhou.github.io/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou

Dependencies:
torch: 0.4
matplotlib
"""
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()

# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)


# default network
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

if __name__ == '__main__':
    # different nets
    net_SGD         = Net()
    net_Momentum    = Net()
    net_RMSprop     = Net()
    net_Adam        = Net()
    nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

    # different optimizers
    opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
    opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
    opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
    opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
    optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

    loss_func = torch.nn.MSELoss()
    losses_his = [[], [], [], []]   # record loss

    # training
    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        for step, (b_x, b_y) in enumerate(loader):          # for each training step
            for net, opt, l_his in zip(nets, optimizers, losses_his):
                output = net(b_x)              # get output for every net
                loss = loss_func(output, b_y)  # compute loss for every net
                opt.zero_grad()                # clear gradients for next train
                loss.backward()                # backpropagation, compute gradients
                opt.step()                     # apply gradients
                l_his.append(loss.data.numpy())     # loss recoder

    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his in enumerate(losses_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('Steps')
    plt.ylabel('Loss')
    plt.ylim((0, 0.2))
    plt.show()

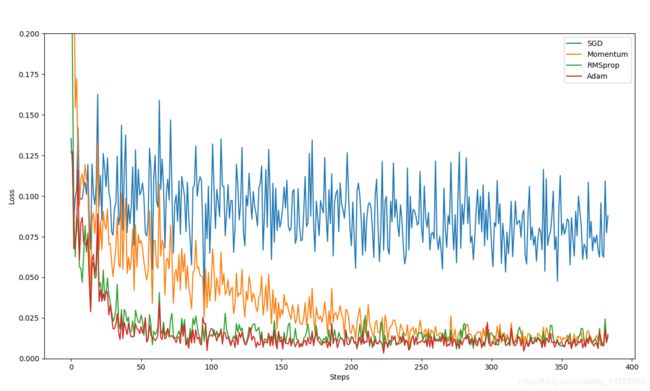
可以看到SGD相对还是比较慢的,可以尝试其它的算法,对应查其参数.

4.1 CNN 卷积神经网络

"""
View more, visit my tutorial page: https://morvanzhou.github.io/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou

Dependencies:
torch: 0.4
torchvision
matplotlib
"""
# library
# standard library
import os

# third-party library
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 1               # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 50
LR = 0.001              # learning rate
DOWNLOAD_MNIST = False


# Mnist digits dataset
if not(os.path.exists('./mnist/')) or not os.listdir('./mnist/'):
    # not mnist dir or mnist is empyt dir
    DOWNLOAD_MNIST = True

train_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,                                     # this is training data
    transform=torchvision.transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                                                    # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,
)

# plot one example
print(train_data.train_data.size())                 # (60000, 28, 28)
print(train_data.train_labels.size())               # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()

# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

# pick 2000 samples to speed up testing
test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255.   # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)
test_y = test_data.test_labels[:2000]


class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(         # input shape (1, 28, 28)
            nn.Conv2d(
                in_channels=1,              # input height
                out_channels=16,            # n_filters
                kernel_size=5,              # filter size
                stride=1,                   # filter movement/step
                padding=2,                  # if want same width and length of this image after Conv2d, padding=(kernel_size-1)/2 if stride=1
            ),                              # output shape (16, 28, 28)
            nn.ReLU(),                      # activation
            nn.MaxPool2d(kernel_size=2),    # choose max value in 2x2 area, output shape (16, 14, 14)
        )
        self.conv2 = nn.Sequential(         # input shape (16, 14, 14)
            nn.Conv2d(16, 32, 5, 1, 2),     # output shape (32, 14, 14)
            nn.ReLU(),                      # activation
            nn.MaxPool2d(2),                # output shape (32, 7, 7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)   # fully connected layer, output 10 classes

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)           # flatten the output of conv2 to (batch_size, 32 * 7 * 7)
        output = self.out(x)
        return output, x    # return x for visualization


cnn = CNN()
print(cnn)  # net architecture

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss()                       # the target label is not one-hotted

# following function (plot_with_labels) is for visualization, can be ignored if not interested
from matplotlib import cm
try: from sklearn.manifold import TSNE; HAS_SK = True
except: HAS_SK = False; print('Please install sklearn for layer visualization')
def plot_with_labels(lowDWeights, labels):
    plt.cla()
    X, Y = lowDWeights[:, 0], lowDWeights[:, 1]
    for x, y, s in zip(X, Y, labels):
        c = cm.rainbow(int(255 * s / 9)); plt.text(x, y, s, backgroundcolor=c, fontsize=9)
    plt.xlim(X.min(), X.max()); plt.ylim(Y.min(), Y.max()); plt.title('Visualize last layer'); plt.show(); plt.pause(0.01)

plt.ion()
# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):   # gives batch data, normalize x when iterate train_loader

        output = cnn(b_x)[0]               # cnn output
        loss = loss_func(output, b_y)   # cross entropy loss
        optimizer.zero_grad()           # clear gradients for this training step
        loss.backward()                 # backpropagation, compute gradients
        optimizer.step()                # apply gradients

        if step % 50 == 0:
            test_output, last_layer = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y.data.numpy()).astype(int).sum()) / float(test_y.size(0))
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
            if HAS_SK:
                # Visualization of trained flatten layer (T-SNE)
                tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
                plot_only = 500
                low_dim_embs = tsne.fit_transform(last_layer.data.numpy()[:plot_only, :])
                labels = test_y.numpy()[:plot_only]
                plot_with_labels(low_dim_embs, labels)
plt.ioff()

# print 10 predictions from test data
test_output, _ = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

torchvision中包含一些数据库

• 建立CNN网络的类中,self.conv1定义第一个卷积层,一般一个卷积网络的一层就包括nn.Conv2d()一个过滤器,一个激活函数,一个池化层.
  nn.Conv2d()中的in_channels参数表示图片的通道数,out_channels是输出filter的个数;kernel_size定义filter的宽和高;stride表示filter跳跃的步长;padding看边缘填充的层数.
  nn.MaxPool2d()建立池化层,kernel_size定义池化层的大小
  self.out中定义一个线性输出层,nn.Linear()中的10代表输出的10个label;一开始图片的维度为12828,经过第一层之后变成了162828(因为使用了padding,所以长和宽没有变),经过第一层的池化层,长和宽减少一半,变成161414,再通过第二层的池化,长和宽又减少一半,最后变为3277.
  在forward()函数中,x的尺寸会考虑batch,维度为(batch,32,7,7)通过view()来改变x的维度成batch327*7,使其输入到输出层

4.2 RNN 循环神经网络 分类

import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt


# torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 1               # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28          # rnn time step / image height
INPUT_SIZE = 28         # rnn input size / image width
LR = 0.01               # learning rate
DOWNLOAD_MNIST = True   # set to True if haven't download the data


# Mnist digital dataset
train_data = dsets.MNIST(
    root='./mnist/',
    train=True,                         # this is training data
    transform=transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                                        # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,            # download it if you don't have it
)

# plot one example
print(train_data.train_data.size())     # (60000, 28, 28)
print(train_data.train_labels.size())   # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()

# Data Loader for easy mini-batch return in training
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

# convert test data into Variable, pick 2000 samples to speed up testing
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255.   # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000]    # covert to numpy array


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.LSTM(         # if use nn.RNN(), it hardly learns
            input_size=INPUT_SIZE,
            hidden_size=64,         # rnn hidden unit
            num_layers=1,           # number of rnn layer
            batch_first=True,       # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
        )

        self.out = nn.Linear(64, 10)

    def forward(self, x):
        # x shape (batch, time_step, input_size)
        # r_out shape (batch, time_step, output_size)
        # h_n shape (n_layers, batch, hidden_size)
        # h_c shape (n_layers, batch, hidden_size)
        r_out, (h_n, h_c) = self.rnn(x, None)   # None represents zero initial hidden state

        # choose r_out at the last time step
        out = self.out(r_out[:, -1, :])
        return out


rnn = RNN()
print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss()                       # the target label is not one-hotted

# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):        # gives batch data
        b_x = b_x.view(-1, 28, 28)              # reshape x to (batch, time_step, input_size)

        output = rnn(b_x)                               # rnn output
        loss = loss_func(output, b_y)                   # cross entropy loss
        optimizer.zero_grad()                           # clear gradients for this training step
        loss.backward()                                 # backpropagation, compute gradients
        optimizer.step()                                # apply gradients

        if step % 50 == 0:
            test_output = rnn(test_x)                   # (samples, time_step, input_size)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)

# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')

同样在最开始先定义一些超参数，如BATCH_SIZE批训练的数量，TIME_STEP和INPUT_SIZE都为28，因为每次读取图片的一行，总共读取28行。
使用nn.LSTM可以创建LSTM网络，·batch_first表示是batch成为第一个维度。

 r_out, (h_n, h_c) = self.rnn(x, None)

在定义的forward函数中，传入的数据的shape(batch,time_step,input_size)，完成每一个step的input。
r_out中会存储从第一步到最后一步的outout。
h_n, h_c表示返回的hidden_state,可以看作每学习一次，神经网络所学到的理解，下一个step再学习的时候，除了下一次的input就还需要传入这一次的hidden state。这里有两个hidden state，一个是分线程的，一个是主线程的。None表示首先的hidden state有没有。
最后的输出要选择最后一个output，self.out(r_out[:,-1,:])

4.3 RNN 循环神经网络(回归)

"""
View more, visit my tutorial page: https://morvanzhou.github.io/tutorials/
My Youtube Channel: https://www.youtube.com/user/MorvanZhou

Dependencies:
torch: 0.4
matplotlib
numpy
"""
import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# Hyper Parameters
TIME_STEP = 10      # rnn time step
INPUT_SIZE = 1      # rnn input size
LR = 0.02           # learning rate

# show data
steps = np.linspace(0, np.pi*2, 100, dtype=np.float32)  # float32 for converting torch FloatTensor
x_np = np.sin(steps)
y_np = np.cos(steps)
plt.plot(steps, y_np, 'r-', label='target (cos)')
plt.plot(steps, x_np, 'b-', label='input (sin)')
plt.legend(loc='best')
plt.show()


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.RNN(
            input_size=INPUT_SIZE,
            hidden_size=32,     # rnn hidden unit
            num_layers=1,       # number of rnn layer
            batch_first=True,   # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h_state):
        # x (batch, time_step, input_size)
        # h_state (n_layers, batch, hidden_size)
        # r_out (batch, time_step, hidden_size)
        r_out, h_state = self.rnn(x, h_state)

        outs = []    # save all predictions
        for time_step in range(r_out.size(1)):    # calculate output for each time step
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state

        # instead, for simplicity, you can replace above codes by follows
        # r_out = r_out.view(-1, 32)
        # outs = self.out(r_out)
        # outs = outs.view(-1, TIME_STEP, 1)
        # return outs, h_state
        
        # or even simpler, since nn.Linear can accept inputs of any dimension 
        # and returns outputs with same dimension except for the last
        # outs = self.out(r_out)
        # return outs

rnn = RNN()
print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.MSELoss()

h_state = None      # for initial hidden state

plt.figure(1, figsize=(12, 5))
plt.ion()           # continuously plot

for step in range(100):
    start, end = step * np.pi, (step+1)*np.pi   # time range
    # use sin predicts cos
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32, endpoint=False)  # float32 for converting torch FloatTensor
    x_np = np.sin(steps)
    y_np = np.cos(steps)

    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])    # shape (batch, time_step, input_size)
    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])

    prediction, h_state = rnn(x, h_state)   # rnn output
    # !! next step is important !!
    h_state = h_state.data        # repack the hidden state, break the connection from last iteration

    loss = loss_func(prediction, y)         # calculate loss
    optimizer.zero_grad()                   # clear gradients for this training step
    loss.backward()                         # backpropagation, compute gradients
    optimizer.step()                        # apply gradients

    # plotting
    plt.plot(steps, y_np.flatten(), 'r-')
    plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
    plt.draw(); plt.pause(0.05)

plt.ioff()
plt.show()