强化学习基础 | (16) 深度确定性策略梯度(DDPG)

原文地址

在A3C中，我们讨论了使用多线程的方法来解决Actor-Critic难收敛的问题，今天我们不使用多线程，而是使用和DDQN类似的方法：即经验回放和双网络的方法来改进Actor-Critic难收敛的问题，这个算法就是深度确定性策略梯度(Deep Deterministic Policy Gradient，以下简称DDPG)。

本篇主要参考了DDPG的论文和ICML 2016的deep RL tutorial。

1. 从随机策略到确定性策略

从DDPG这个名字看，它是由D（Deep）+D（Deterministic ）+ PG(Policy Gradient)组成。PG(Policy Gradient)我们在策略梯度(Policy Gradient)里已经讨论过。那什么是确定性策略梯度(Deterministic Policy Gradient，以下简称DPG)呢？

确定性策略是和随机策略相对而言的，对于某一些动作集合来说，它可能是连续值，或者非常高维的离散值，这样动作的空间维度极大。如果我们使用随机策略，即像DQN一样研究它所有的可能动作的概率，并计算各个可能的动作的价值的话，那需要的样本量是非常大才可行的。于是有人就想出使用确定性策略来简化这个问题。

作为随机策略，在相同的策略，在同一个状态处，采用的动作是基于一个概率分布的，即是不确定的。而确定性策略则决定简单点，虽然在同一个状态处，采用的动作概率不同，但是最大概率只有一个，如果我们只取最大概率的动作，去掉这个概率分布，那么就简单多了。即作为确定性策略，相同的策略，在同一个状态处，动作是唯一确定的，即策略变成

2. 从DPG到DDPG

在看确定性策略梯度DPG前，我们看看基于Q值的随机性策略梯度的梯度计算公式：

其中状态的采样空间为${\rho }^{\pi }$,${\Delta }_{\theta }\log {\pi }_{\theta }(s,a)$是分值函数，可见随机性策略梯度需要在整个动作的空间${\pi }_{\theta }$进行采样。

而DPG基于Q值的确定性策略梯度的梯度计算公式是：

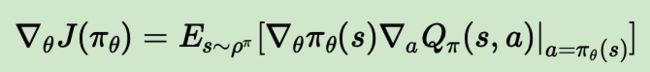
跟随机策略梯度的式子相比，少了对动作的积分，多了回报Q函数对动作的导数。

而从DPG到DDPG的过程，完全可以类比DQN到DDQN的过程。除了老生常谈的经验回放以外，我们有了双网络，即当前网络和目标网络的概念。而由于现在我们本来就有Actor网络和Critic两个网络，那么双网络后就变成了4个网络，分别是：Actor当前网络，Actor目标网络，Critic当前网络，Critic目标网络。2个Actor网络的结构相同，2个Critic网络的结构相同。那么这4个网络的功能各自是什么呢？

3. DDPG的原理

DDPG有4个网络，在了解这4个网络的功能之前，我们先复习DDQN的两个网络：当前Q网络和目标Q网络的作用。可以复习Double DQN (DDQN)。

DDQN的当前Q网络负责对当前状态S使用ϵ−贪婪法选择动作A，执行动作A,获得新状态S’和奖励R,将样本放入经验回放池，对经验回放池中采样的下一状态S’使用贪婪法选择动作A’，供目标Q网络计算目标Q值(把选择动作和计算Q值解耦)，当目标Q网络计算出目标Q值后，当前Q网络会进行网络参数的更新，并定期把最新网络参数复制到目标Q网络（延时更新）。

DDQN的目标Q网络则负责基于经验回放池计算目标Q值,提供给当前Q网络用，目标Q网络会定期从当前Q网络复制最新网络参数。

现在我们回到DDPG，作为DDPG，Critic当前网络，Critic目标网络和DDQN的当前Q网络，目标Q网络的功能定位基本类似，但是我们有自己的Actor策略网络，因此不需要ϵ−贪婪法这样的选择方法，这部分DDQN的功能到了DDPG可以在Actor当前网络完成。而对经验回放池中采样的下一状态S’使用贪婪法选择动作A’，这部分工作由于用来估计目标Q值，因此可以放到Actor目标网络完成。

基于经验回放池和目标Actor网络提供的S’,A’计算目标Q值的一部分，这部分由于是评估，因此还是放到Critic目标网络完成。而Critic目标网络计算出目标Q值一部分后，Critic当前网络会计算目标Q值，并进行网络参数的更新，并定期将网络参数复制到Critic目标网络。

此外，Actor当前网络也会基于Critic目标网络计算出的目标Q值，进行网络参数的更新，并定期将网络参数复制到Actor目标网络。

有了上面的思路，我们总结下DDPG 4个网络的功能定位：

1）Actor当前网络：负责策略网络参数$\theta$的迭代更新，负责根据当前状态S选择当前动作A，用于和环境交互生成S’,R。
2）Actor目标网络：负责根据经验回放池中采样的下一状态S’,选择最优下一动作A’。网络参数${\theta }^{\prime }$定期从$\theta$复制。
3）Critic当前网络：负责价值网络参数w的迭代更新，负责计算负责计算当前Q值Q(S,A,w)。目标Q值$y_i=R+\gamma Q^{\prime }(S^{\prime },A^{\prime },w^{\prime })$
4）Critic目标网络：负责计算目标Q值中的$Q^{\prime }(S^{\prime },A^{\prime },w^{\prime })$部分。网络参数w’定期从w复制。

DDPG除了这4个网络结构，还用到了经验回放，这部分用于计算目标Q值，和DQN没有什么区别，这里就不展开了。

此外，DDPG从当前网络到目标网络的复制和我们之前讲到了DQN不一样。回想DQN，我们是直接把将当前Q网络的参数复制到目标Q网络，即w’=w, DDPG这里没有使用这种硬更新，而是使用了软更新，即每次参数只更新一点点，即

其中$\tau$是更新系数，一般取的比较小，比如0.1或者0.01这样的值。

同时，为了学习过程可以增加一些随机性，增加学习的覆盖，DDPG对选择出来的动作A会增加一定的噪声$\mathcal{N}$,即最终和环境交互的动作A的表达式是：

最后，我们来看看DDPG的损失函数。对于Critic当前网络，其损失函数和DQN是类似的，都是均方误差，即：

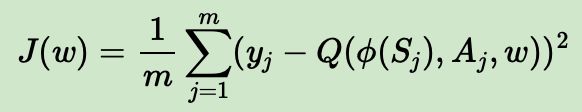
而对于 Actor当前网络，其损失函数就和之前讲的PG，A3C不同了，这里由于是确定性策略，原论文定义的损失梯度是：

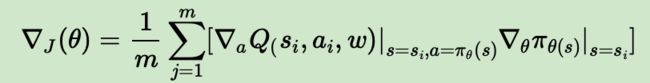
这个可以对应上我们第二节的确定性策略梯度，看起来比较麻烦，但是其实理解起来很简单。假如对同一个状态，我们输出了两个不同的动作$a_1$和$a_2$，从Critic当前网络得到了两个反馈的Q值，分别是$Q_1,Q_2$,假设$Q_1>Q_2$, 即采取动作$a_1$可以得到更多的奖励，那么策略梯度的思想是什么呢，就是增加$a_1$的概率，降低$a_2$的概率，也就是说，Actor想要尽可能的得到更大的Q值。所以我们的Actor的损失可以简单的理解为得到的反馈Q值越大损失越小，得到的反馈Q值越小损失越大，因此只要对状态估计网络返回的Q值取个负号即可，即：

4. DDPG算法流程

这里我们总结下DDPG的算法流程

输入：Actor当前网络，Actor目标网络，Critic当前网络，Critic目标网络,参数分别为$\theta ,{\theta }^{\prime },w,w^{\prime }$,衰减因子$\gamma$,软更新系数$\tau$,批量梯度下降的样本数m,目标Q网络参数更新频率C。最大迭代次数T。随机噪音函数$\mathcal{N}$

输出：最优Actor当前网络参数$\theta$,Critic当前网络参数$w$

1）随机初始化$\theta ,w$, w’=w,${\theta }^{\prime }=\theta$。清空经验回放的集合D
2）for i from 1 to T，进行迭代。
a）初始化S为当前状态序列的第一个状态, 拿到其特征向量$\varphi (S)$
b）在Actor当前网络基于状态S得到动作$A={\pi }_{\theta }(\varphi (S))+\mathcal{N}$
c）执行动作A,得到新状态S’,奖励R,是否终止状态$is\_end$
d）将$\{\varphi (S),A,R,\varphi (S^{\prime }),is\_end\}$这个五元组存入经验回放集合D
e）S = S’
f）从经验回放集合D中采样m个样本$\{\varphi (S_j),A_j,R_j,\varphi (S_j^{\prime }),is\_en{d}_j\},j=1,2,...,m$,计算当前目标Q值$y_j$:

g）使用均方差损失函数$\frac{1}{m}{\sum }_{j=1}^m(y_j-Q(\varphi (S_j),A_j,w){)}^2$,通过神经网络的梯度反向传播来更新Critic当前网络的所有参数w
h）使用$J(\theta )=-\frac{1}{m}{\sum }_{j=1}^{m}Q(s_i,a_i,\theta )$, 通过神经网络的梯度反向传播来更新Actor当前网络的所有参数$\theta$
i）如果T%C=1,则更新Critic目标网络和Actor目标网络参数：

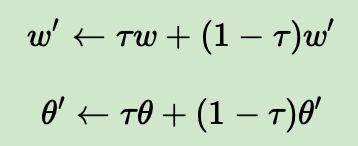
j）如果S’是终止状态，当前轮迭代完毕，否则转到步骤b)
以上就是DDPG算法的主流程，要注意的是上面2.f中的${\pi }_{{\theta }^{\prime }}(\varphi (S_j^{\prime }))$是通过Actor目标网络得到，而$Q^{\prime }(\varphi (S_j^{\prime }),{\pi }_{{\theta }^{\prime }}(\varphi (S_j^{\prime })),w^{\prime })$.

5. DDPG实例

这里我们给出DDPG第一个算法实例，代码主要参考自莫烦的Github代码。增加了测试模型效果的部分，优化了少量参数。

完整代码

这里我们没有用之前的CartPole游戏，因为它不是连续动作。我们使用了Pendulum-v0这个游戏。目的是用最小的力矩使棒子竖起来，这个游戏的详细介绍参见这里。输入状态是角度的sin，cos值，以及角速度。一共三个值。动作是一个连续的力矩值。

两个Actor网络和两个Critic网络的定义参见：

def _build_a(self, s, scope, trainable):
        with tf.variable_scope(scope):
            net = tf.layers.dense(s, 30, activation=tf.nn.relu, name='l1', trainable=trainable)
            a = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, name='a', trainable=trainable)
            return tf.multiply(a, self.a_bound, name='scaled_a')

    def _build_c(self, s, a, scope, trainable):
        with tf.variable_scope(scope):
            n_l1 = 30
            w1_s = tf.get_variable('w1_s', [self.s_dim, n_l1], trainable=trainable)
            w1_a = tf.get_variable('w1_a', [self.a_dim, n_l1], trainable=trainable)
            b1 = tf.get_variable('b1', [1, n_l1], trainable=trainable)
            net = tf.nn.relu(tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1)
            return tf.layers.dense(net, 1, trainable=trainable)  # Q(s,a)

Actor当前网络和Critic当前网络损失函数的定义参见：

td_error = tf.losses.mean_squared_error(labels=q_target, predictions=q)
self.ctrain = tf.train.AdamOptimizer(LR_C).minimize(td_error,var_list=self.ce_params)

a_loss = - tf.reduce_mean(q)    # maximize the q
self.atrain = tf.train.AdamOptimizer(LR_A).minimize(a_loss,var_list=self.ae_params)

Actor目标网络和Critic目标网络参数软更新，Actor当前网络和Critic当前网络反向传播更新部分的代码如下：

def learn(self):
        # soft target replacement
        self.sess.run(self.soft_replace)

        indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE)
        bt = self.memory[indices, :]
        bs = bt[:, :self.s_dim]
        ba = bt[:, self.s_dim: self.s_dim + self.a_dim]
        br = bt[:, -self.s_dim - 1: -self.s_dim]
        bs_ = bt[:, -self.s_dim:]

        self.sess.run(self.atrain, {self.S: bs})
        self.sess.run(self.ctrain, {self.S: bs, self.a: ba, self.R: br, self.S_: bs_})

其余的可以对照算法和代码一起学习，应该比较容易理解。

6. DDPG总结

DDPG参考了DDQN的算法思想吗，通过双网络和经验回放，加一些其他的优化，比较好的解决了Actor-Critic难收敛的问题。因此在实际产品中尤其是自动化相关的产品中用的比较多，是一个比较成熟的Actor-Critic算法。

到此，我们的Policy Based RL系列也讨论完了，而在更早我们讨论了Value Based RL系列，至此，我们还剩下Model Based RL没有讨论。后续我们讨论Model Based RL的相关算法。