MATLAB中的视角处理
view命令用来控制三维图形的观察点和视角,它的使用格式如下:
调用格式 说明
view(az,el) 给三维空间图形设置观察点的方位角az与仰角el
view([az,el]) 同上
view([x,y,z]) 将点(x,y,z)设置为视点
view(2) 设置默认的二维形式视点,其中az = 0,el = 90,即从z轴上方观看
view(3) 设置默认的三维形式视点,其中az = -37.5, ell = 30
view(T) 根据转换矩阵T设置视点,其中T为4*4阶的矩阵,如同用命令viewmtx生成的透视转换矩阵一样(注意:在2014版本中,这条命令好像没了)
[az,el]=view 返回当前的方位角az与仰角el
T = view 返回当前的4*4阶的转换矩阵T
方位角az与仰角el为这样两个旋转角度:作一通过视点与z轴的平面,则该平面与x-y平面有一交线,该交线与y轴的反方向的、换逆时针方向(从z轴的方向观察)计算的、单位为度的夹角,就是观察点的方位角az;若角度为负值,则按顺时针方向计算。在通过视点与z轴的平面上,用一直线连接视点与坐标原点,该直线与x-y平面的夹角就是观察点的仰角el;若仰角为负值,则观察点转换到曲面下面:
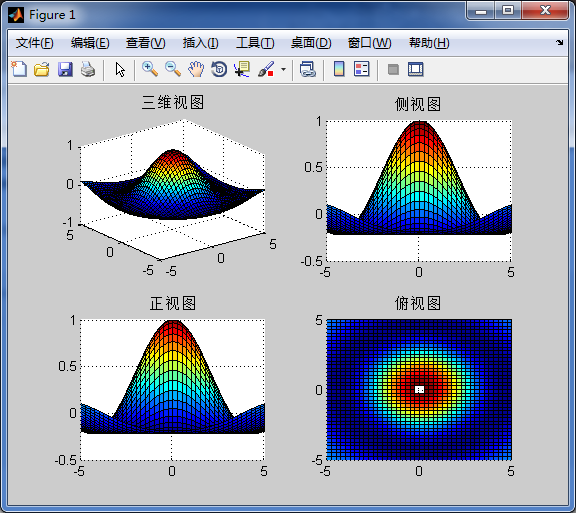
例:在同一窗口中绘制下面函数的各种视图
>> [X,Y] = meshgrid(-5:0.25:5);
>> Z = sin(sqrt(X.^2+Y.^2))./sqrt(X.^2+Y.^2);
>> subplot(2,2,1)
>> surf(X,Y,Z),title('三维视图')
>> subplot(2,2,2)
>> surf(X,Y,Z),view(90,0)
>> title('侧视图')
>> subplot(2,2,3)
>> surf(X,Y,Z),view(0,0)
>> title('正视图')
>> subplot(2,2,4)
>> surf(X,Y,Z),view(0,90)
>> title('俯视图')
>> 
在描述view命令的使用格式时提到了viewmtx命令,该命令用来计算一个4*4阶的正交的或透视的转换矩阵,该矩阵将一个四维向量转换到一个二维的视平面上。
viewmtx命令的使用格式如下:
调用格式 说明
T = viewmtx(az,el) 返回一与视点的方位角az与仰角el(单位都为度)对应的正交矩阵,但不改变当前视点
T = viewmtx(az,el,phi) 返回一透视的转换矩阵。其中参量phi是单位为度的透视角度,为标准化立方体(单位为度)的对像视角角度与透视扭曲程序
T = viewmtx(az,el,phi,xc) 返回一在标准化的图形立方体中的点xc为目标点的透视矩阵(就像相机正对着点xc一样),目标点xc为视角的中心点。用户可以
用一三维向量xc = [xc, yc ,zc]指定该中心点,每一分量都在区间[0,1]上,默认值为xc = [0 0 0]
其中phi的取值及说明见下表:
phi的取值 说明
0° 正交投影
10° 类似于远距离投影
25° 类似于普通投影
60° 类似于广角投影
利用这个命令,用户可以通过使用其返回的矩阵。
