计算机视觉--张氏相机标定法测定手机相机参数
实验拍摄设备
iPhone xr 64G
张氏相机标定法原理
我们相机拍摄照片是将3维世界中的图像通过相机的转化为2维的图像。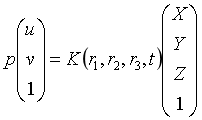
其中u,v是相机中的坐标,X,Y,Z是世界坐标,r是表示旋转的矩阵。这是世界坐标到像平面坐标的公式。
传统的方法需要我们制作一个精度极高的标定板,碍于技术限制,这种传统的方法在自己做实验时并不适用,因为我们不能制作出精度如此高的标定板。张正友提出的方法是打印出如博文一开始的棋盘图,因为棋盘黑白相间,且距离我们自己可控,所以在通过角点的检测就能找到这些角点在图像中的坐标。而对与世界坐标的认定,我们将这个棋盘看成是XOY这个平面,所以我们只需要设定一个世界坐标的原点,就会得知每个棋盘角点在世界坐标的坐标信息。
import cv2
import glob
import numpy as np
cbraw = 11
cbcol = 7
prepare object points, like (0,0,0), (1,0,0), (2,0,0) …,(6,5,0)
objp = np.zeros((cbraw*cbcol,3), np.float32)
objp[:,:2] = np.mgrid[0:cbraw,0:cbcol].T.reshape(-1,2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
#glob是个文件名管理工具
images = glob.glob("*.jpg")
for fname in images:
#对每张图片,识别出角点,记录世界物体坐标和图像坐标
img = cv2.imread(fname) #source image
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转灰度
#寻找角点,存入corners,ret是找到角点的flag
ret, corners = cv2.findChessboardCorners(gray,(11,7),None)
#criteria:角点精准化迭代过程的终止条件
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#执行亚像素级角点检测
corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
objpoints.append(objp)
imgpoints.append(corners2)
#在棋盘上绘制角点,只是可视化工具
img = cv2.drawChessboardCorners(gray,(6,4),corners2,ret)
cv2.imshow('img',img)
#cv2.waitKey(1000)
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
img = cv2.imread(‘9.jpg’)
h,w = img.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
#纠正畸变
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
#这步只是输出纠正畸变以后的图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite(‘calibresult.png’,dst)
#打印我们要求的两个矩阵参数
print “newcameramtx:\n”,newcameramtx
print “dist:\n”,dist
#计算误差
tot_error = 0
for i in xrange(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
tot_error += error
print "total error: ", tot_error/len(objpoints)
实验结果:

其中newcameramtx是上文提到的K这个矩阵的值,dist是畸变系数,这里的五个系数可以用来消除径向畸变和切向畸变。total error是重投影误差,可以用来检测畸变参数的误差。