深入浅出递归思想
引言
作为一名程序员,算法是不可或缺的。每个人对算法的敏感度不一样,就想每个人对数学的敏感度一样,有些人逻辑能力就是很强。有一说一,博主个人觉得自己的数学学的不咋滴,但是像我这样笨笨的人,我可以多复习,多推演嘛。今天我想写的是关于递归的理解和使用,我会介绍一下递归的规则,然后用简单和比较难的例子进行学习。
技术点:
1、递归是函数对自身的调用,调用分为直接调用和间接调用,直接调用是指在函数体中调用自身,间接调用是调用别的函数,而这些别的函数又调用函数本身。它主要是把大问题变成小问题,使得代码更加简洁。理解递归需要有一定的抽象能力。
何时使用递归
在什么情况下使用递归呢?博主在判断某个需求是否要用递归实现主要分为以下几个步骤:
a、根据需求画图,把流程用图形的形式展现出来,会帮助你理解
b、觉得它是一个递归,那就尝试建立它的数学函数模型
c、用代码进行实现数学函数模型
d、代码推导,与需求是否一致
在知道步骤之后,我们必须要知道递归的几个原则,在这之前,我们有必要知道递归在代码中的骨架是如何的:
method(){
if(条件满足)
return;//结束递归(建立在基准情况之上)
else
method()//继续递归(不断推进)
}a、基准情况:函数出口,也就是说此时的函数的值可以直接算出,不需要通过递归求得。或者理解为最后一次递归操作。
b、不断推进:意思就是说每次进行一次递归,那么下次需要的递归会逐渐靠近基准情况,注意这个逐渐靠近是建立在能到达基准情况的,比如说下面这段递归代码:
package com.bw;
/**
* @author brickworker
* 关于类RecursiveTest的描述:递归展示类
*/
public class RecursiveTest {
public static int run(int k){
if(k == 0)
return 0;
else
return run(k/3+1) +k-1;
}
}
我们通过上述代码理解一下递归规则,首先因为if(k == 0)结束函数调用,说明它具备基准情况。然后我们看下它的不断推进,发现当run(1)执行后又要去求得run(1),使得代码变成了无限循环。难倒你说不靠近基准情况嘛?其实是靠近的,比如说run(10)就要先求的run(4),但是它没有建立在对于run(0)可达的基础之上,所以说这个递归是不合法的。
斐波那契数列
斐波那契数列应该算是递归的经典了,我们就从这个经典作为第一个简单的例子帮大家如何处理递归,写出递归代码:
斐波那契数列是指1,1,2,3,5,8,13,21…的一个数列,它的规律就是某一个数就是前面两个数的只和,博主对于这个数列画图如下:
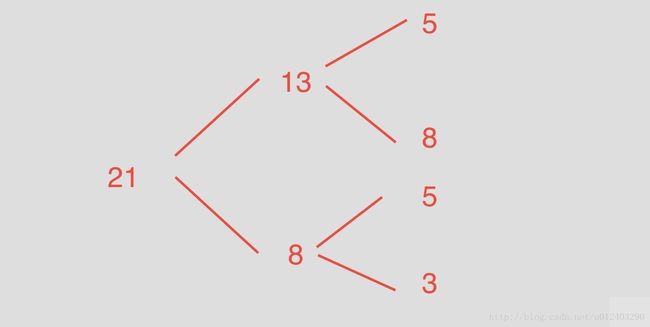
仔细观察上面的图,我觉得它们之间存在一种递归的关系,尝试建立它的数学函数模型,假设21为f(n),那么13就是f(n-1),8就是f(n-2)。那么就可以总结出它们的规律就是f(n) = f(n-1)+f(n-2)在n>=2的情况下。
那么我们马上就可以写出它的代码形式了:
package com.bw;
/**
* @author brickworker
* 关于类RecursiveTest的描述:递归展示类
*/
public class RecursiveTest {
public static int fbnq(int n){
if( n== 2 || n==1)
return 1;
else
return fbnq(n-1)+fbnq(n-2);
}
public static void main(String[] args) {
System.out.println(fbnq(8));
}
}
//输出结果:21最后,我们需要用写出的代码进行验证需求,如果满足需求,递归就完成了从思考,画图,抽象,编写的步骤。其实最后的验证显得非常的不专业和不标准,虽然说特殊不能代表一般,但是我们在现实生活中相信大家很多时候都是用几组数据测试一下吧。
全排列问题
如果说斐波那契数列是递归入门,那么给定一个字符串,输出它的全排列就显得比较困难了。
全排列:
假如输入字符串为qwe,那么输出就是要qwe,qew,wqe,weq,eqw,ewq六种情况。拿到这个问题,之后我们要开始寻找规律了,总共有3个坑位,有3个字母来占坑。那么我们可以抓住坑位来进行分析,画出的图如下:
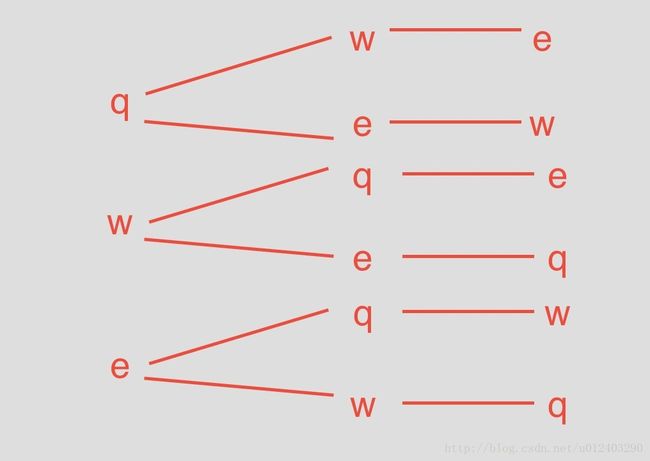
分析题目我们就知道输出的字符长度和输入肯定是一样的,接着从图中可以看出,对所有的字符进行了3次分配,那么我们先考虑第一个坑位,在第一个坑位分配的时候,需要从给出的字符串中任意选择一个字符填入,既然是全排列,所以坑位对于字符的要求肯定是都要有的,所以在这一步可以考虑用for循环添加字符。接下来我们考虑第二个坑位,这个坑位要填入的字符是除却第一个坑位已经用掉的字符所剩下的字符数组中选择一个填入,因为是要求全排列,所以也必然用for循环解决。那么基准情形就是最后一次执行就是还剩下一个字符的时候,直接就放在最后一位。那么,分析到这里我们大致可以推算出这个数学函数模型应该是这样的:
f(char[], int),其中char[]数组表示组合的结果,int值表示处理第几个坑位,同时我们还知道肯定存在一个for循环去处理这个char[]数组,而且需要去除已经使用的字符。不知道博主如此解释,能看懂不?
下面就是博主写的代码,每一句我都写了注释:
package com.bw;
/**
* @author brickworker
* 关于类RecursiveTest的描述:递归展示类
*/
public class RecursiveTest {
public static void permutation(char[] ch, int n){//ch表示重新排列后的字符数组,n表示处理第几个坑位
if(n == ch.length)//基准情形
System.out.println(String.valueOf(ch));
else{
for (int i = n; i < ch.length; i++) {//把n赋值给i用于前面说到的除却已使用的字符
//以下操作其实是进行了字符交换
char temp = ch[n];//把要处理的位置的数据拿出来,防止覆盖
ch[n] = ch[i]; //对第n个坑位进行赋值
ch[i] = temp;//赋值结束之后需要把前面存储的数据赋值给替换的
permutation(ch, n+1);//继续下个坑位赋值]
//因为上面的交换导致ch数组顺序出错,递归以后需要矫正,不然遍历会出错
temp = ch[i];
ch[i] = ch[n];
ch[n] = temp;
}
}
}
public static void main(String[] args) {
permutation("abc".toCharArray(), 0);
}
// 执行结果:
// acb
// bac
// bca
// cba
// cab
}
对于上面的函数代码,已经是非常简便的了,可能中间那块交换的代码比较不好理解,我这里再解释一下,为什么要交换?因为char[]就是你输入的字符串,也是要输出的字符串,所以当对某一个坑位进行赋值的时候,不能覆盖这个坑位原有的字符,所以要把这个要处理的坑位原本的值用temp存储起来。再者为什么迭代后又需要交换回来呢?也是由于因为char[]即是输入也是输出,再循环的过程中,你改变了循环对象本身,如果不改变回来,那么后面的循环就是错误的,操作的不再是原来的数组了。
再者,为什么说上述代码是最简版了,博主考虑了2种处理方法:
1、建立一个char[] temp来接收入参的char[]数组。但是这个方式要注意,即使你char[] temp = ch是不能解决问题的,你只是改变了引用罢了,修改了数组顺序ch也是会变动的。你必须要new一个出来才行,同时代码量很多。
2、处理函数入参,改成f(char[] ch, String result, int n),多一个result来存储结果也可以解决这个问题。大家可以试一试,但是代码就显得一点都不优雅,你觉得呢?
总结
递归其实是非常奇妙的,有的时候压根感觉不到能用递归处理,但是你通过画图分析之后,发现存在一个基准情况,而且通过一步步的推到会靠近这个基准情况。找到这种规律之后,我们需要抽象出一个数学函数模型,然后用代码来实现这个函数模型,编写结束之后,再去验证代码的运行结果是否满足需求。
好啦,今天就写到这里了。如果大家有什么问题可以联系我: