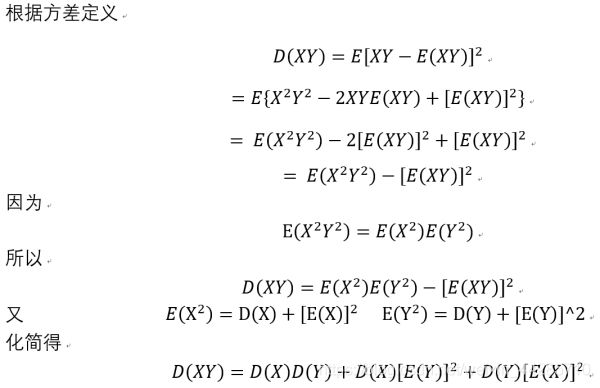pytorch学习笔记:模型创建及权重初始化
1、模型创建
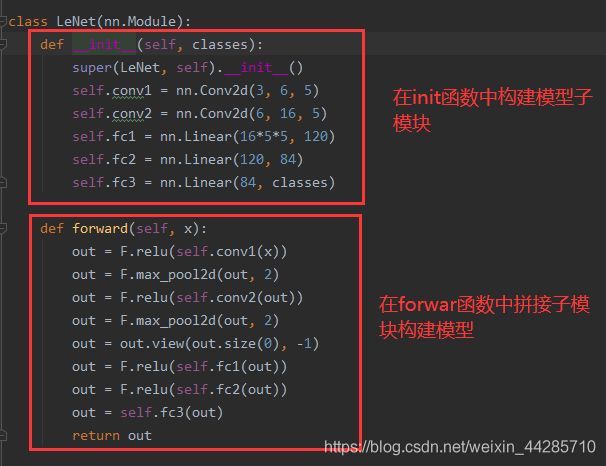
1.1、构建网络层(子模块)
1.2、拼接网络层(子模块)
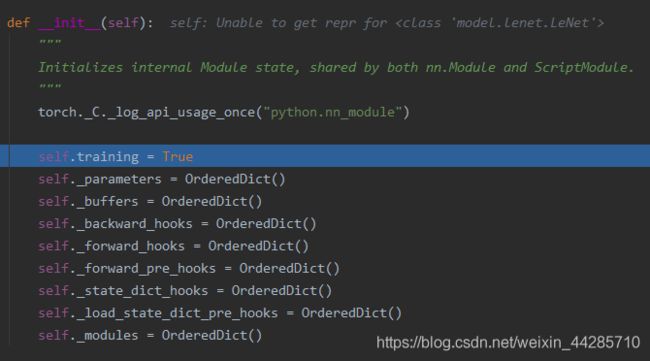
1.3、nn.Module
首先进行了8个有序字典的初始化,用来管理各个参数及网络设置
- 一个module可以包含多个子module
- 一个module相当于一个运算,必须实现forward()函数
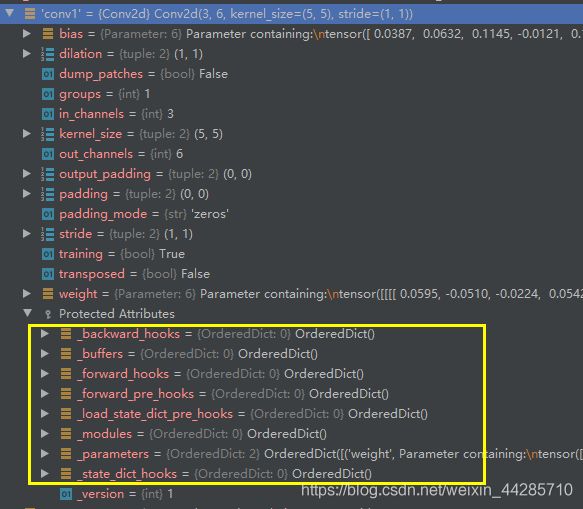
- 每个module都有8个字典管理它的数学
1.4模型容器
1.4.1、nn.Sequetial
功能:按顺序组合网络子模块,自带forward(),通过for循环依次执行前向传播运算
# ============================ Sequential
class LeNetSequential(nn.Module):
def __init__(self, classes):
super(LeNetSequential, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 6, 5),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, 5),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120),
nn.ReLU(),
nn.Linear(120, 84),
nn.ReLU(),
nn.Linear(84, classes),)
def forward(self, x):
x = self.features(x)
x = x.view(x.size()[0], -1)
x = self.classifier(x)
return x创建好的网络结构如下图所示:
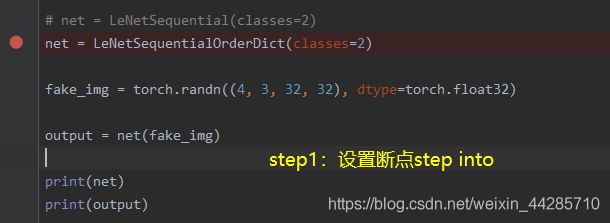
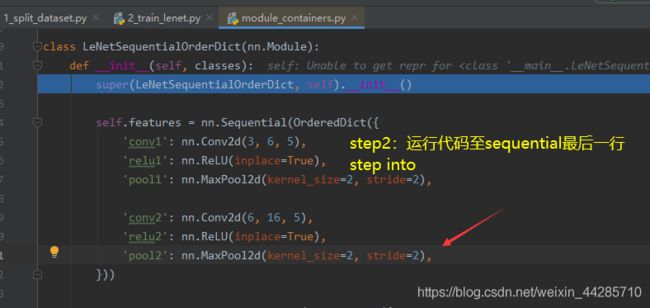
调试观察创建过程的步骤:
- 在网络实例化那行代码step into进入网络定义的类
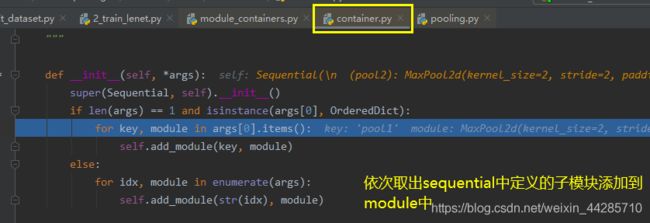
- 进入到定义sequential的部分运行到最后一行代码step into 两次(第一次进入的是最后一个子模块网络的建立,第二次进入sequential的创建)可以看到for循环下取出各个子模块并添加到modules
1.4.2、nn.ModuleList
功能:像python的list一样包装多个网络层,以迭代的方式调用网络层
- append():在modulelist后面添加网络层
- extend():拼接两个modulelist
- insert():在modulelist中指定位置插入网络层
# ============================ ModuleList
class ModuleList(nn.Module):
def __init__(self):
super(ModuleList, self).__init__()
self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(20)])
def forward(self, x):
for i, linear in enumerate(self.linears):
x = linear(x)
return x
net = ModuleList()
print(net)
fake_data = torch.ones((10, 10))
output = net(fake_data)
print(output)1.4.3、nn.ModuleDict
功能:像python的dict一样包装多个网络层(每一个给一个key,可通过key索引网络层)
- clear():清空moduleDict
- items():返回可迭代的键值对(key-value pairs)
- keys():返回字典的key
- values():返回字典的value
- pop():返回一对键值,并从字典中删除
# ============================ ModuleDict
class ModuleDict(nn.Module):
def __init__(self):
super(ModuleDict, self).__init__()
self.choices = nn.ModuleDict({
'conv': nn.Conv2d(10, 10, 3),
'pool': nn.MaxPool2d(3)
})
self.activations = nn.ModuleDict({
'relu': nn.ReLU(),
'prelu': nn.PReLU()
})
def forward(self, x, choice, act):
x = self.choices[choice](x)
x = self.activations[act](x)
return x
net = ModuleDict()
fake_img = torch.randn((4, 10, 32, 32))
output = net(fake_img, 'conv', 'relu')
#prelu输出结果有负值,改为relu后输出没有负数,可以检查是不是按照我们的想法运行的
print(output)创建的时候dict里面的子模块是全部都要创建的,前向传播的时候根据key做出选择。
模型容器总结
- Sequential:顺序性,各网络层之间严格按照顺序执行,常用语block构建
- ModuleList:迭代性,常用于大量重复网络构建,通过for循环实现重复构建
- ModuleDict:索引性,常用于可选择的网络层
1.5、动手搭建AlexNet
模型特点:
- 采用Relu激活函数:替换饱和激活函数,减轻梯度消失
- 采用LRN(局部响应归一化):对数据归一化,减轻梯度消失
- Dropout:提高了全连接层的鲁棒性,增加网络的泛化能力
- 数据增强:TenCrop,色彩修改
pytorch调用一句代码即可实现:
alexnet = torchvision.models.AlexNet()self.features = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(64, 192, kernel_size=5, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(192, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(256, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(256 * 6 * 6, 4096),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, num_classes),
)
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x1.6、卷积层
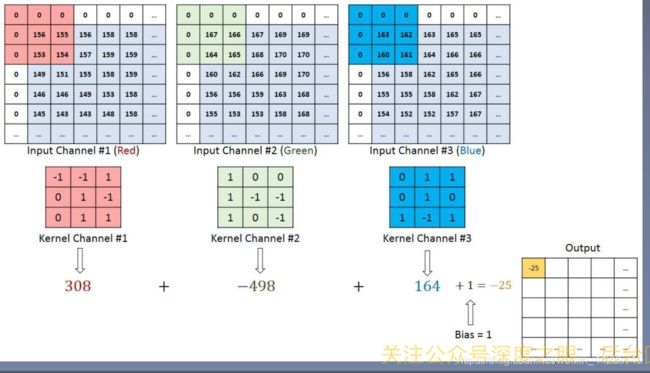
卷积运算:卷积核在输入图像上滑动,相应位置上进行相加。卷积过程类似于用一个模板去图像上寻找与他相似的区域,与卷积核模式越相似,激活值越高,从而实现特征提取。
卷积核:可以认为是某种模式或某种特征
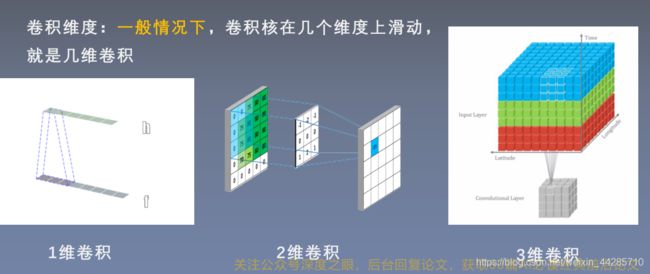
卷积维度:一般情况下,卷积核在几个维度上滑动就是几维卷积
RGB三通道图像卷积计算方式细节:
卷积尺寸计算方式
nn.Conv2d
import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed
set_seed(1) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255
# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W
# ================================= create convolution layer ==================================
# ================ 2d
# flag = 1
flag = 0
if flag:
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)
# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
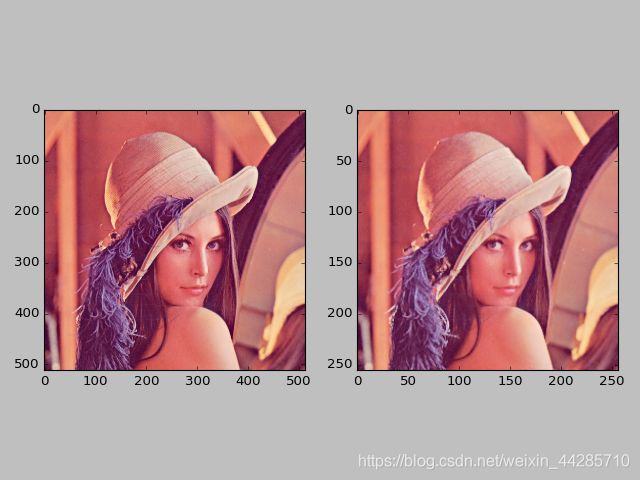
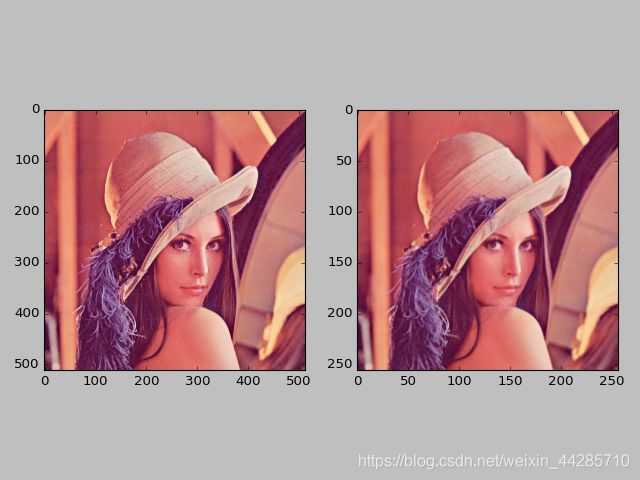
plt.show()卷积后结果展示
1.7、转置卷积(反卷积)
功能:用于对图像进行上采样,物体检测任务经常用到(不可逆过程,转置卷积得到的图像与原图不相等)
import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed
set_seed(1) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255
# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W
# ================================= create convolution layer ==================================
# ================ transposed
flag = 1
# flag = 0
if flag:
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2) # input:(i, o, size)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
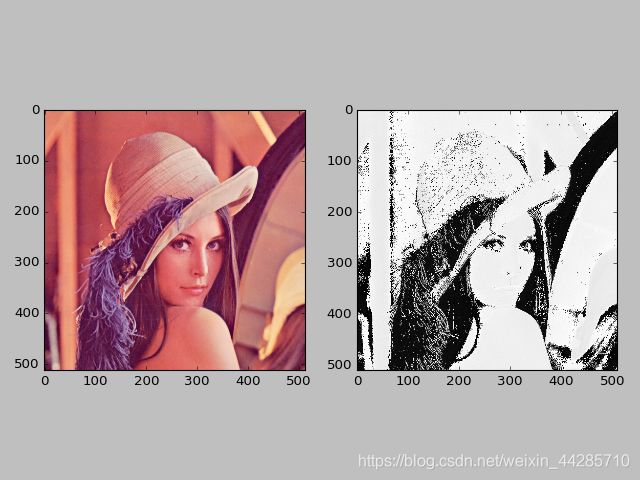
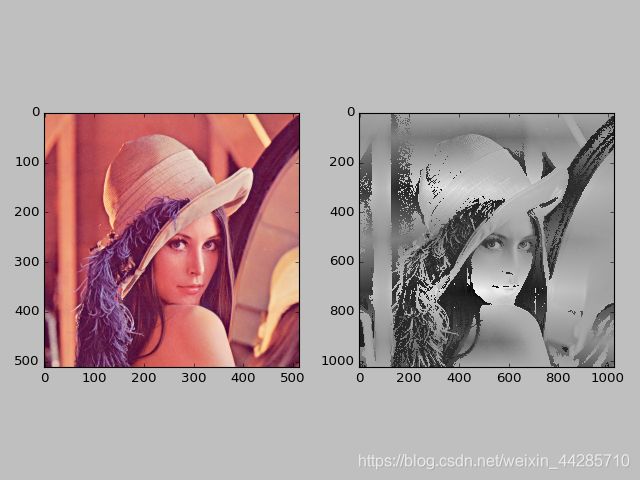
plt.show()上采样结果展示
步长设置为3产生棋盘效应,由于不均匀重叠导致的。
棋盘效应的解释与解决方法:推荐文章《 Deconvolution and Checkerboard Artifacts》
1.8、池化层
池化运算:对输入信号(图像)进行“收集”(多变少)并“总结”(max,mean),类似水池收集水资源。
divisor_override:正常情况池化区域的像素相加除以像素个数,设置这个参数可以改变除数
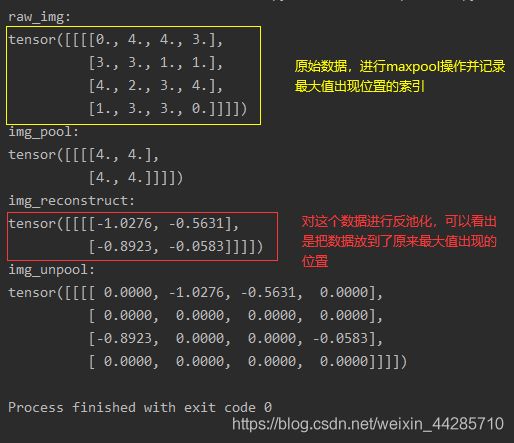
1.8、反最大值池化(上采样)
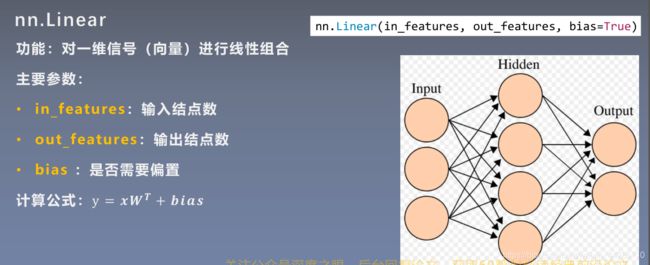
1.9、全连接层
每一个神经元与上一层所有神经元相连,实现对上一层的线性组合。
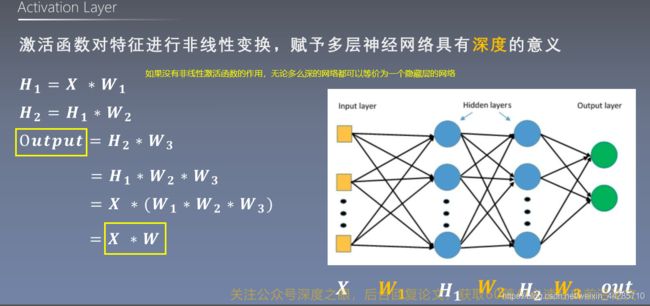
1.10、激活函数
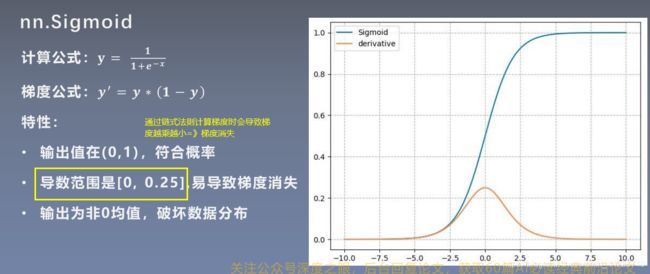
Sigmoid函数
Relu函数(线性修正单元)
为了解决死神经元的问题,提出了三种改进方式
2、权值初始化
适当的权值初始化可以加速模型的训练和模型的收敛,而错误的权值初始化会导致梯度消失/爆炸,从而无法完成网络的训练,因此需要控制网络输出值的尺度范围【】。
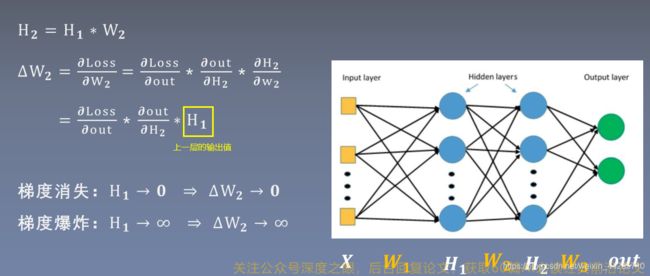
2.1梯度消失于梯度爆炸
从公式的角度可以看出,要避免梯度消失或爆炸就要严格控制网络输出层输出值的尺度范围。
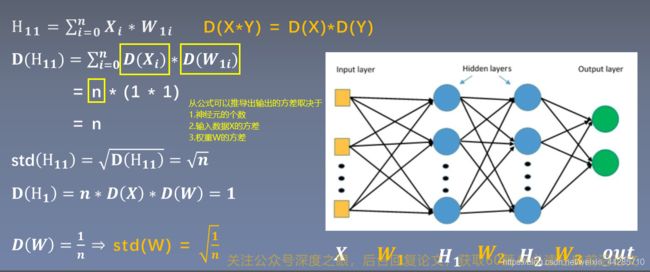
对于无激活函数的全连接层,假设权重W与输入X相互独立,且均服从于0均值1标准差的正态分布(期望为0),因此公式可以简化如下
从上图中的公式可以看出,每传播一层,输出值数据的方差就会扩大n 倍,要想控制输出H的尺度范围,只需要控制H的方差为1,则无论经过多少层都可以维持在初始输入X的方差附近,因此权重w需要初始化方差为1/n(n为神经元的个数)
100层的全连接网络,每层256个神经元,权重初始化为0均值1标准差,各层输出的标准差结果如下,从下列的数据也可以看出每经过一层,标准差扩大根号n倍(16)
layer:0, std:15.959932327270508
layer:1, std:256.6237487792969
layer:2, std:4107.24560546875
layer:3, std:65576.8125
layer:4, std:1045011.875
layer:5, std:17110408.0
layer:6, std:275461408.0
layer:7, std:4402537984.0
layer:8, std:71323615232.0
layer:9, std:1148104736768.0
layer:10, std:17911758454784.0
layer:11, std:283574846619648.0
layer:12, std:4480599809064960.0
layer:13, std:7.196814275405414e+16
layer:14, std:1.1507761512626258e+18
layer:15, std:1.853110740188555e+19
layer:16, std:2.9677725826641455e+20
layer:17, std:4.780376223769898e+21
layer:18, std:7.613223480799065e+22
layer:19, std:1.2092652108825478e+24
layer:20, std:1.923257075956356e+25
layer:21, std:3.134467063655912e+26
layer:22, std:5.014437766285408e+27
layer:23, std:8.066615144249704e+28
layer:24, std:1.2392661553516338e+30
layer:25, std:1.9455688099759845e+31
layer:26, std:3.0238180658999113e+32
layer:27, std:4.950357571077011e+33
layer:28, std:8.150925520353362e+34
layer:29, std:1.322983152787379e+36
layer:30, std:2.0786820453988485e+37
layer:31, std:nan
output is nan in 31 layers
tensor([[ inf, -2.6817e+38, inf, ..., inf,
inf, inf],
[ -inf, -inf, 1.4387e+38, ..., -1.3409e+38,
-1.9659e+38, -inf],
[-1.5873e+37, inf, -inf, ..., inf,
-inf, 1.1484e+38],
...,
[ 2.7754e+38, -1.6783e+38, -1.5531e+38, ..., inf,
-9.9440e+37, -2.5132e+38],
[-7.7184e+37, -inf, inf, ..., -2.6505e+38,
inf, inf],
[ inf, inf, -inf, ..., -inf,
inf, 1.7432e+38]], grad_fn=)
Process finished with exit code 0
100层的全连接网络,每层256个神经元,权重初始化为0均值,标准差为根号(1/n)时,各层输出的标准差结果如下,可以看出每层输出值的标准差都能维持在1附近
layer:0, std:0.9974957704544067
layer:1, std:1.0024365186691284
layer:2, std:1.002745509147644
layer:3, std:1.0006227493286133
layer:4, std:0.9966009855270386
layer:5, std:1.019859790802002
layer:6, std:1.026173710823059
layer:7, std:1.0250457525253296
layer:8, std:1.0378952026367188
layer:9, std:1.0441951751708984
layer:10, std:1.0181655883789062
layer:11, std:1.0074602365493774
layer:12, std:0.9948930144309998
layer:13, std:0.9987586140632629
layer:14, std:0.9981392025947571
layer:15, std:1.0045733451843262
layer:16, std:1.0055204629898071
layer:17, std:1.0122840404510498
layer:18, std:1.0076017379760742
layer:19, std:1.000280737876892
layer:20, std:0.9943006038665771
layer:21, std:1.012800931930542
layer:22, std:1.012657642364502
layer:23, std:1.018149971961975
layer:24, std:0.9776086211204529
layer:25, std:0.9592394828796387
layer:26, std:0.9317858815193176
layer:27, std:0.9534041881561279
layer:28, std:0.9811319708824158
layer:29, std:0.9953019022941589
layer:30, std:0.9773916006088257
layer:31, std:0.9655940532684326
layer:32, std:0.9270440936088562
layer:33, std:0.9329946637153625
layer:34, std:0.9311841726303101
layer:35, std:0.9354336261749268
layer:36, std:0.9492132067680359
layer:37, std:0.9679954648017883
layer:38, std:0.9849981665611267
layer:39, std:0.9982335567474365
layer:40, std:0.9616852402687073
layer:41, std:0.9439758658409119
layer:42, std:0.9631161093711853
layer:43, std:0.958673894405365
layer:44, std:0.9675614237785339
layer:45, std:0.9837557077407837
layer:46, std:0.9867278337478638
layer:47, std:0.9920817017555237
layer:48, std:0.9650403261184692
layer:49, std:0.9991624355316162
layer:50, std:0.9946174025535583
layer:51, std:0.9662044048309326
layer:52, std:0.9827387928962708
layer:53, std:0.9887880086898804
layer:54, std:0.9932605624198914
layer:55, std:1.0237400531768799
layer:56, std:0.9702046513557434
layer:57, std:1.0045380592346191
layer:58, std:0.9943899512290955
layer:59, std:0.9900636076927185
layer:60, std:0.99446702003479
layer:61, std:0.9768352508544922
layer:62, std:0.9797843098640442
layer:63, std:0.9951220750808716
layer:64, std:0.9980446696281433
layer:65, std:1.0086933374404907
layer:66, std:1.0276142358779907
layer:67, std:1.0429234504699707
layer:68, std:1.0197855234146118
layer:69, std:1.0319130420684814
layer:70, std:1.0540012121200562
layer:71, std:1.026781439781189
layer:72, std:1.0331352949142456
layer:73, std:1.0666675567626953
layer:74, std:1.0413838624954224
layer:75, std:1.0733673572540283
layer:76, std:1.0404183864593506
layer:77, std:1.0344083309173584
layer:78, std:1.0022705793380737
layer:79, std:0.99835205078125
layer:80, std:0.9732587337493896
layer:81, std:0.9777462482452393
layer:82, std:0.9753198623657227
layer:83, std:0.9938382506370544
layer:84, std:0.9472599029541016
layer:85, std:0.9511011242866516
layer:86, std:0.9737769961357117
layer:87, std:1.005651831626892
layer:88, std:1.0043526887893677
layer:89, std:0.9889539480209351
layer:90, std:1.0130352973937988
layer:91, std:1.0030947923660278
layer:92, std:0.9993206262588501
layer:93, std:1.0342745780944824
layer:94, std:1.031973123550415
layer:95, std:1.0413124561309814
layer:96, std:1.0817031860351562
layer:97, std:1.128799557685852
layer:98, std:1.1617802381515503
layer:99, std:1.2215303182601929
tensor([[-1.0696, -1.1373, 0.5047, ..., -0.4766, 1.5904, -0.1076],
[ 0.4572, 1.6211, 1.9659, ..., -0.3558, -1.1235, 0.0979],
[ 0.3908, -0.9998, -0.8680, ..., -2.4161, 0.5035, 0.2814],
...,
[ 0.1876, 0.7971, -0.5918, ..., 0.5395, -0.8932, 0.1211],
[-0.0102, -1.5027, -2.6860, ..., 0.6954, -0.1858, -0.8027],
[-0.5871, -1.3739, -2.9027, ..., 1.6734, 0.5094, -0.9986]],
grad_fn=)
Process finished with exit code 0
当神经元个数设置为400时,标准差与手动计算结果一致(每经过一层,标准差扩大20倍)
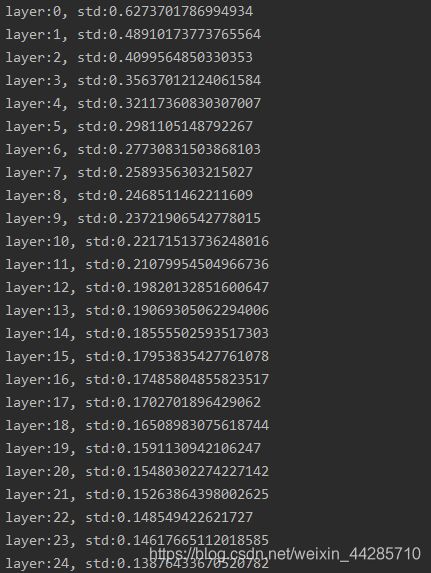
当全连接层采用tanh的激活函数时,标准差越来越小,从而会造成梯度消失
2.2、加入激活函数的权重初始化
- Xavier初始化适用于饱和激活函数
n_i为输入层神经元个数,n_i+1为输出层神经元个数,通常Xavier采用均匀分布进行初始化。
import os
import torch
import random
import numpy as np
import torch.nn as nn
def set_seed(seed=1):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
set_seed(1) # 设置随机种子
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
x = torch.tanh(x)
print("layer:{}, std:{}".format(i, x.std()))
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
#xavier手动计算
a = np.sqrt(6 / (self.neural_num + self.neural_num))
tanh_gain = nn.init.calculate_gain('tanh') #计算增益
a *= tanh_gain
nn.init.uniform_(m.weight.data, -a, a)
#调用pytorch实现xavier初始化,适用于饱和激活函数
# tanh_gain = nn.init.calculate_gain('tanh')
# nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
# flag = 0
flag = 1
if flag:
layer_nums = 100
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
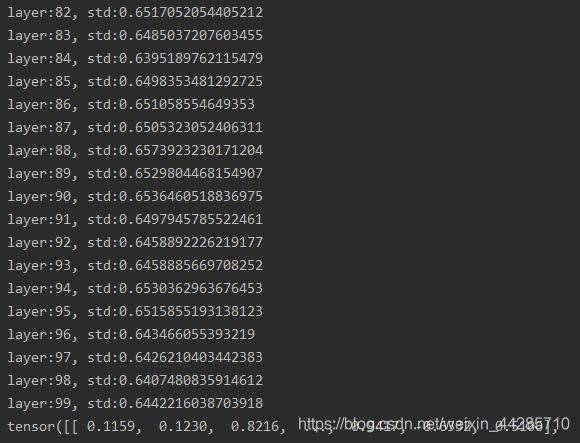
print(output)可以看到输出数据的标准差能维持在一个范围内
- kaiming初始化方法适用于RuLU及其变种的非饱和激活函数
import os
import torch
import random
import numpy as np
import torch.nn as nn
def set_seed(seed=1):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
set_seed(1) # 设置随机种子
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
x = torch.relu(x)
print("layer:{}, std:{}".format(i, x.std()))
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
#kaiming初始化手动
nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))
#kaiming初始化
# nn.init.kaiming_normal_(m.weight.data)
# flag = 0
flag = 1
if flag:
layer_nums = 100
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
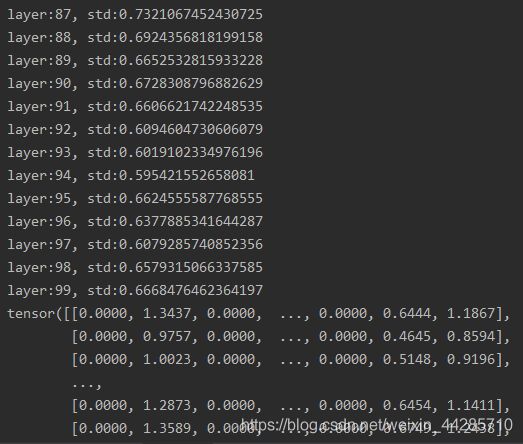
print(output)网络输出结果如下图所示,输出数据标准差能维持在一个稳定的范围内,输出值也比较正常
方差变化尺度=输入数据的方差/输出数据的方差
# ==================== calculate gain ==============================
# flag1 = 0
flag1 = 1
if flag1:
x = torch.randn(10000)
out = torch.tanh(x)
gain = x.std() / out.std()
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)输出结果为