数据分析真题日刷 | 商汤科技2018校招C++/算法开发/大数据/后端/运维/测试/数据挖掘开发工程师笔试第二场
断了大半个月没有刷题,进入「数据分析真题日刷」系列第13篇 。
- 今日真题
商汤科技2018校招C++/算法开发/大数据/后端/运维/测试/数据挖掘开发工程师笔试第二场 (来源:牛客网) - 题型
客观题:单选5道,填空5道
主观题:编程3道 - 完成时间
120分钟 - 牛客网评估难度系数
3颗星
❤️ 「更多数据分析真题」
《数据分析真题日刷 | 目录索引》
1. 交换机主要工作在()?
网络层
数据链路层
物理层
传输层
答案:B
?OSI七层模型涉及的主要设备
- 物理层的主要设备:中继器、集线器、光纤。
- 数据链路层主要设备:交换机、网桥
- 网络层主要设备:路由器
- 举一反三
《京东2019校招数据分析工程师笔试题》第24题。
2. 一个数据表express(No, SenderName, ReceiverName, SenderAddress, ReceiverAddress, Charge, Weight, Type),以下不能完成对应操作的sql语句是()?
查询所有重量在10kg以下的快递,并输出单号和收费
Select No, Charge From express Where Weight < 10
查询所有寄件人第一个字为“李”的快递单
Select * From express Where name like “李%”
统计表中快递单共有多少种类型
Select count(*) From (Select Type From express)
统计表中不同类型的快递单的平均重量,并按从大到小排列
Select Type, avg(Weight) From express Group by Type Order by avg(Weight)
官方答案:C
民间答案:B C D
「题目解析」
B:没有name字段,应该是SenderName;
C:我认为 Type应该去重, Select DISTINCT Type From express
D:Order by 默认升序,不满足从大到小排序。
3. ⼀个完全⼆叉树中有330个叶子节点, 则在该⼆叉树中的节点个数为()?
659
660
可能为659或者660
不可能为659和660
正确答案:C
?二叉树 & 满二叉树 & 完全二叉树 & 平衡二叉树 &二叉排序树
个人总结(不到位的勿喷!)
- 二叉树: 每个结点不超过2个子树的树结构。
- 满二叉树:一个结点要么是叶子节点,要么有两个叶子结点。
- 完全二叉树:深度为h,除h层外,h-1层是满二叉树,h层结点连续集中在左边。
- 平衡二叉树(AVL树):左右子树高度不超过1.
- 二叉排序树(二叉查找树):左结点比根结点小,右结点比根结点大。
————————————————
原文链接:https://blog.csdn.net/a1173537204/article/details/87881286
?完全二叉树性质
完全二叉树中度为1的结点数为1或0。
? 度和结点的关系
树中结点数 = 总分叉数 +1
即,度为0的节点数为度为2的节点数加1
故,n0 = n2 + 1
「题目解析」
已知,n0 = 330
因为 n0 = n2 + 1,所以n2 = 329。
根据性质「完全二叉树中度为1的结点数为1或0」,n1 = 0 或 1
所以,n = n0 + n1 + n2 = 330 + n1 + 329 = 659 + n1 = 659 或 660
4. 假设有一种无色的特殊颜料,与红色颜料混合后会变紫色,与黄色颜料混合会变为绿色,与红色、黄色颜料一起混合会变为黑色,发生颜色变化需要1小时。现有700瓶特殊颜料,其中一瓶已经变质,不管与什么颜料混合都会变为白色。只有一小时时间, 最少需要多少个调色盘才能找出变质的特殊颜料?
10
5
6
16
正确答案:A
「题目解析」
这题本质就是问 —— 至少需要多少个二进制位能够表示出所有的700瓶颜料编号?
因为 2 ^ 9 = 521, 2 ^ 10 =1024, 所以至少需要10个调色盘。
具体理解:
10个二进制位代表10个调色盘,
700瓶颜料从1-700编号,
如果该颜料涂上某个调色盘,则该调色盘记为1。
这样,10个调色盘的结果,都唯一对应着某一个颜料。
0000000000 ~ 颜料1号什么也不涂;
0000000001 ~ 颜料2号涂在第一个调色盘;
0000000010 ~ 颜料3号只涂在第2个调色盘;
0000000011 ~ 颜料4号涂在第1和第2个调色盘 ;
……
所以第一个调色盘上,会涂上所有对应位置为1所对应的颜料。
「其中一瓶已经变质,不管与什么颜料混合都会变为白色」,依据此判断结果。
例如,10个调色盘中,仅有调色盘1和2,同时变白,则4号颜料是变质的。
- 强烈参考
《你只有 10 只小白鼠和一星期的时间,如何检验出哪个瓶子里有毒药?》
5. 一个口袋装着若干蓝球和若干红球,随机抽出两个球。第一个球是蓝球的概率为0.5; 第一球是蓝球且第二个球是红球的概率为0.2。现如果已知第一个球是蓝球,则第二个球是红球的概率是多少?
0.4
0.2
0.1
0.5
正确答案:A
?条件概率
6. 一个狗妈妈有70块肉,狗宝宝距离狗妈妈60步。每次狗妈妈最多拿40块肉,每走2步需要吃掉一块肉,则它最多能把 ?块肉拿给狗宝宝。
答案:20
「民间解析」
根据题意,如果满载直接到终点会浪费掉30肉,而最优解一定要将这30肉消耗掉,以换取满载的情况下距离宝宝最近,因此一定要在起点与终点之间有一个折返点;
设:起点为O、折返点为A、终点为B。OA距离为X,最后剩余Y肉给宝宝;则:
- 第一次从O满载出发再返回有:40-(X/2)*2肉留在A点
- 第二次O载30肉出发到A点捡起第一次留下的肉应该满载:30-X/2+(40-(X/2)*2)=40得到X=20
- 则Y=70-(3x+(60-x))/2,代入x=20得Y=20
————————————————作者:腹肌五块半(▼へ▼メ)
来源:https://www.nowcoder.com/test/question/done?tid=26261351&qid=226008#summary
7. 101枚硬币中有一枚假币,有一个无砝码的天平,在最坏情况下最少称?次,可以判断假币比真币重还是轻。
答案:2
「民间解析」
将硬币按A组(50)、B组(50)、C组(1)分组,先比较A、B两组:
若A=B,则C为假币,再用A或B中任一个与C比,C重则假币重,C轻则真币重;
若A!=B,则A或B中含假币,将A组一分为二:A1(25)、A2(25),比较A1、A2:
1).若A1=A2,则A为真币,故:A>B => 真币重;A 假币重
2).若A1!=A2,则A含假币,故:A 真币重;A>B => 假币重
作者:亻固ヽㄐ生
来源:https://www.nowcoder.com/test/question/done?tid=26261351&qid=226009#summary
问题点在于确认劣质硬币是偏重或偏轻,把所有硬币当作砝码,
- 首先说最好的情况,第一次天枰两边先各放50枚,如果说左右两边平衡,那么剩下第101枚正好就是劣质硬币,第二次把劣质硬币放任意一边即可确认这枚劣质硬币是重或轻。(总共称两次)
- 最坏的情况,在第一次称,左右两边各50枚硬币,左右不平衡,说明劣质硬币在这一百枚里面其中一个,那么仍然只需再称一次即可确认是劣质硬币是重或轻,任意取一边的50枚分别放在天枰两边,打个比方,如果你取便轻的那一端的50枚,分两半放天枰上,如果左右平衡则说明劣质硬币再另一端偏重的50中,即确认劣质硬币偏重。故最坏的情况也只需称2次。
作者:自由王国
来源:https://www.nowcoder.com/test/question/done?tid=26261351&qid=226009#summary
「举一反三」
如果题目变成 —— 有101枚硬币,不知道假币是轻还是重,最少需要多少次才能确保找到这枚假币?
一次天枰称量能够得到左倾、右倾、平衡3种情况,如果把一次称量当做是一次编码,则它是3进制编码才能够表示;
我们想要用3进制编码表示的是:101枚硬币,且假币的轻重未知。
每枚硬币都可能是假币,共101种情况,假币有可能比真币轻,也有可能重,共101*2=202种情况;
3^5=243 则n至少为5才可以。
所以从信息论的角度讲,5次称量是最小值。
- 强烈参考
《天平与假币的算法思考》
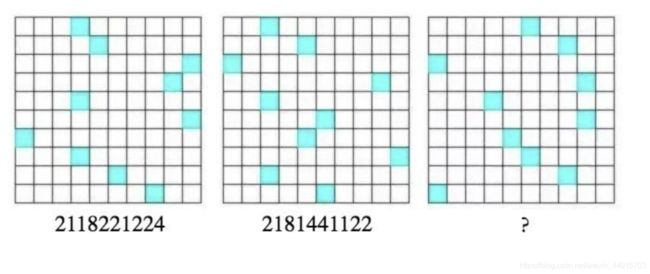
8. 问号处应该为?
答案:4112241441
「题目解析」
竖着每一列,对应一个数字。10列,因此为10位数。
对应法则:2^ (该列蓝色方格的数量)。比如第一个幅图,第一列一个蓝色方格,故对应数字为2^ (1) = 2。
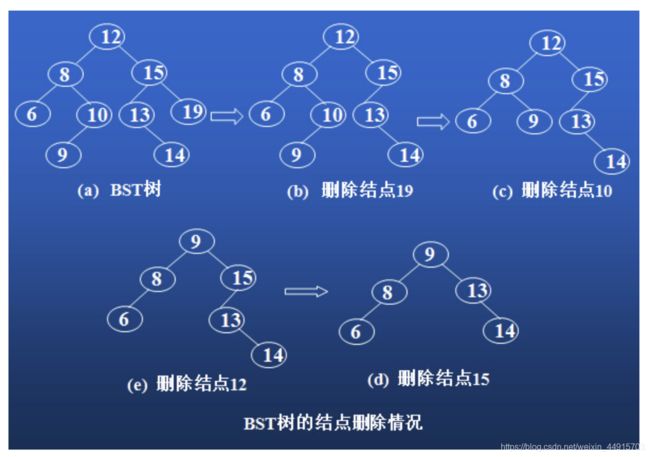
9. 给定数组 [ 48,8,20,72,65,17,28,23 ],构造一棵左子节点 < 父节点 < 右子节点 的二叉搜索树(Binary Search Tree)。把数字48删除,使用前序节点调整后,则数字28的左子节点是数字?。
答案:8
?二叉查找数的删除操作
在二叉查找树删去一个结点,分三种情况讨论:
- 若p是叶子结点: 直接删除p,如图(b)所示。
- 若p只有一棵子树(左子树或右子树):直接用p的左子树(或右子树)取代p的位置而成为f的一棵子树。即原来p是f的左子树,则p的子树成为f的左子树;原来p是f的右子树,则p的子树成为f的右子树,如图©、 (d)所示。
- 若p既有左子树又有右子树 :处理方法有以下两种,可以任选其中一种。
- 用p的直接前驱结点代替p。即从p的左子树中选择值最大的结点s放在p的位置(用结点s的内容替换结点p内容),然后删除结点s。s是p的左子树中的最右边的结点且没有右子树,对s的删除同②,如图(e)所示。
- 用p的直接后继结点代替p。即从p的右子树中选择值最小的结点s放在p的位置(用结点s的内容替换结点p内容),然后删除结点s。s是p的右子树中的最左边的结点且没有左子树,对s的删除同②。
来源:https://www.cnblogs.com/wuyudong/p/binary-search-tree.html
「题目解析」
根据二叉搜索树定义,数组 [ 48,8,20,72,65,17,28,23 ]构建出如下二叉树,
根据删除操作的,第三种情况的第一个处理方法 —— 48的左子树中选择最大的结点28放在48的未知,删除48。
调整后的二叉树,
10. 请阅读以下代码和输入,写出程序的输出结果。
#include
using namespace std;
int main( ) {
const int MAX_N = 1000;
int n, ans;
int a[MAX_N], f[MAX_N];
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> a[i];
f[i] = 1;
for (int j = 0; j < i; ++j) {
if ((a[j] < a[i]) && (f[j] >= f[i]))
f[i] = f[j] + 1;
}
}
ans = 0;
for (int i = 1; i < n; ++i) {
if (f[i] > ans) ans = f[i];
}
cout << ans << endl;
}
答案:5
「民间解析」
最长升序列个数,了解一下。
每个 f [ i ] 代表从 a[0] 开始到 a[i] 之间,有多少个数小于等于 a[i] 并且是 升序的,例子中的:
10
2 5 13 6 7 4 10 3 5 8,
2,5,6,7,10这五个是最长升序列,所以输出5
作者:放学后我不走~
来源:https://www.nowcoder.com/profile/159098729/test/26261351/226012#summary
(求评论区详解~)
11. 有一种将字母编码成数字的方式:‘a’->1, ‘b->2’, … , ‘z->26’。现在给一串数字,给出有多少种可能的译码结果。
12. 给定四个空杯子,容量分别为S1 S2 S3 S4,允许进行以下操作:
-
将某个杯子接满水
-
将某个杯子里的水全部倒掉
-
将杯子A中的水倒进杯子B,直到A倒空或者B被倒满
问最少要多少步操作才能使得这四个杯子装的水分别为T1 T2 T3 T4
13. 研究地球空间科学的永强想研究海岸线的长度和海岸线面积之间的关系,为此他找来了很多航拍图像。在航拍图像上利用图像分割的方法,把图像的每个像素标记成陆地(1)和水面(0)。
已知每张图最底部的一条边都是陆地,并且在一张图上陆地都是四邻域联通的。
但是永强发现分割的结果有很多的噪声,于是他定义了如下规则试图去除噪声:
a) 如果一个水面区域被陆地包围,则将这个区域记为陆地;
b) 在a的基础上如果一个陆地区域不和底边的陆地相连,那么这是一个岛屿,不计入陆地的面积。