红黑树(C++代码实现+原理简介)
Red-Black Tree
本文根据<
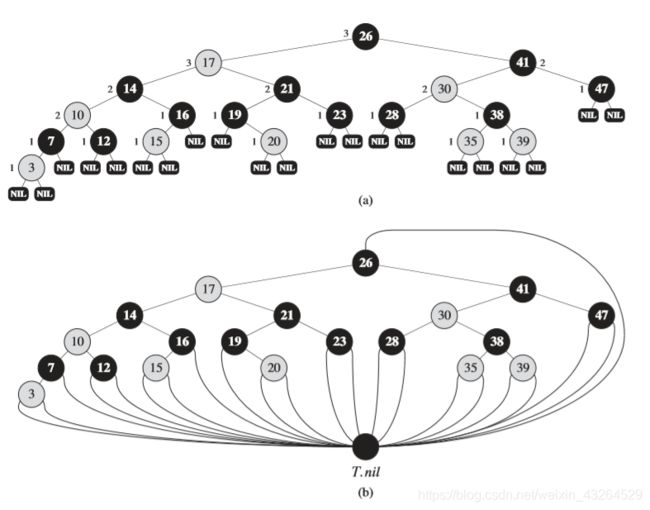
红黑树需要满足的五条性质
- 所有点都是红色/黑色的;
- 根节点是黑色的;
- 所有叶子节点都是黑色的;
- 对于红色节点,它的儿子节点都是黑色的;
- 对于每一个节点x,从x节点到x往下的所有叶子的简单路径上的黑色节点数量相同(称该数量为the black height of node, 记为 b h ( x ) bh(x) bh(x))。
引理 13.1
一棵具有 n n n个内部节点的红黑树的高度至多为 2 l g ( n + 1 ) 2lg(n+1) 2lg(n+1).
证明:
对根节点 x x x,有 n ≥ ( 2 b h ( x ) − 1 ) + ( 2 b h ( x ) − 1 ) + 1 n≥(2^{bh(x)} -1)+(2^{bh(x)} -1)+1 n≥(2bh(x)−1)+(2bh(x)−1)+1
n ≥ 2 b h ( x ) − 1 n≥2^{bh(x)}-1 n≥2bh(x)−1
2 × b h ( x ) ≥ h ( x ) 2\times bh(x)≥h(x) 2×bh(x)≥h(x) //考虑从根到叶子节点的一条简单路径是红黑相间的情况;
h ( x ) ≤ 2 l g ( n + 1 ) h(x)≤2lg(n+1) h(x)≤2lg(n+1)
数据结构定义
const static bool RED = 0;
const static bool BLACK = 1;
struct Node
{
int val;
bool color; //颜色
Node *left, *right, *p; //左,右孩子,父节点
Node(const int &v,const bool &c=RED,Node *l=nullptr, Node *r=nullptr, Node *_p = nullptr)
:val(v),color(c),left(l),right(r),p(_p){}
};
struct RBTree
{
Node *root; //树根
Node *nil; //外部节点, color: 黑色
RBTree()
{
nil = new Node(-1, BLACK, nil, nil, nil);
root = nil;
}
};
二叉搜索树的基本操作
void left_rotate(Node* x) //左旋
{
Node *y = x->right;
x->right = y->left;
if(y->left != nil)
{
y->left->p = x;
}
y->p = x->p;
if(x->p == nil)
root = y;
else if(x->p->left == x)
x->p->left = y;
else
x->p->right = y;
x->p = y;
y->left = x;
}
Right Rotation右旋
void right_rotate(Node* x) //右旋
{
Node *y = x->left;
x->left = y->right;
if(y->right != nil)
y->right->p = x;
y->p = x->p;
if(x->p == nil)
root = y;
else if(x->p->left == x)
x->p->left = y;
else
x->p->right = y;
x->p = y;
y->right = x;
}
Insert 插入
Node* insert_bst(Node* &p, Node* &r, const int &v)
{
if(r == nil) //树为空时
{
r = new Node(v, RED, nil, nil, p);
if( p == nil )
root = r;
if(v > p->val)
p->right = r;
else
p->left = r;
}
else //树非空
{
if(v < r->val)
return insert_bst(r, r->left, v);
else
return insert_bst(r, r->right, v);
}
return r;
}
红黑树操作
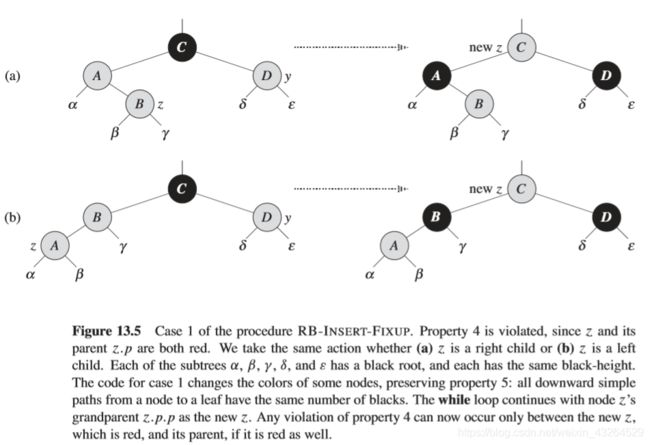
RB-Insert = 二叉搜索树的插入+插入修复(insert_fixup)

void insert(const int &v)
{
Node* z = insert_bst(nil, root, v);
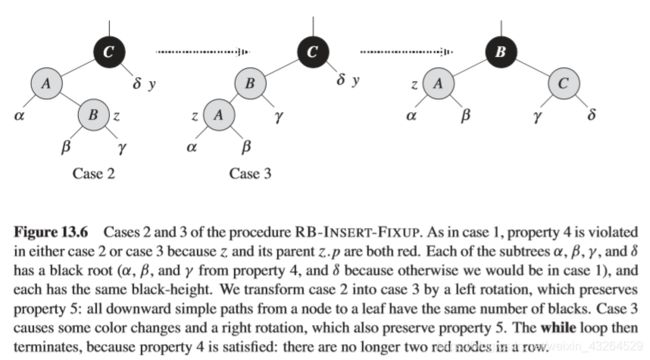
//下面是insert_fixup,分为3x2=6种情况,以对称的视角来看,则只有三种。
while(z->p->color==RED)
{
if(z->p->p->left == z->p)
{
if(z->p->p->right->color == RED) //A: CASE 1
{
z->p->color = BLACK;
z->p->p->color = RED;
z->p->p->right->color = BLACK;
z = z->p->p;
}
else
{
if(z->p->right == z) //A: CASE 2
{
z = z->p;
left_rotate(z);
} //A: CASE 3
z->p->color = BLACK;
z->p->p->color = RED;
right_rotate(z->p->p);
}
}
else
{
if(z->p->p->left->color == RED) //B: CASE 1
{
z->p->color = BLACK;
z->p->p->color = RED;
z->p->p->left->color = BLACK;
z = z->p->p;
}
else
{
if(z->p->left == z) //B: CASE 2
{
z = z->p;
right_rotate(z);
}
z->p->color = BLACK; //B: CASE 3
z->p->p->color = RED;
left_rotate(z->p->p);
}
}
}
root->color = BLACK; //把根的颜色设置为BLACK
}
RB-delete删除 = 二叉树的删除+删除修复(delete_fixup)
做二叉树删除时,需要记录被删除节点的颜色。
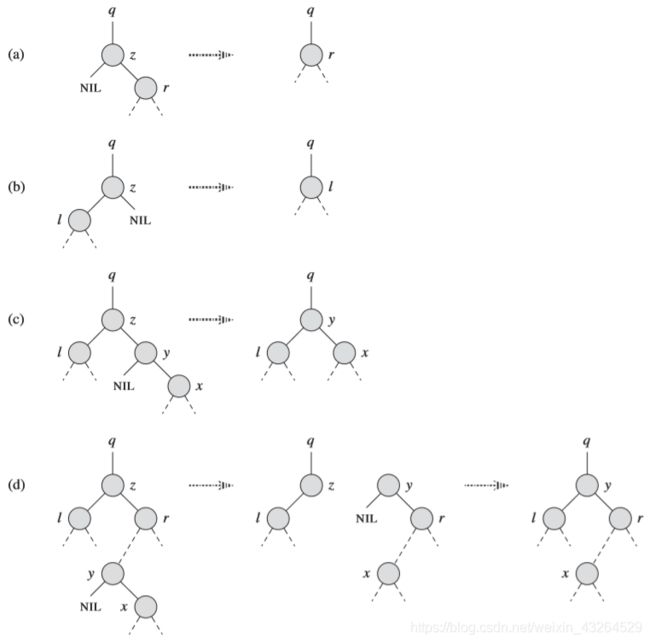
二叉搜索树删除的四种情况(按教材上的写法实现的,自己一般习惯写只需要考虑三种情况的删除写法。)
辅助函数
Node* find_min(Node *r)
{
Node *p = r;
while(r!=nil)
{
p = r;
r = r->left;
}
return p;
}
void rb_transplant(Node* &u, Node* &v)
{
if( u->p == nil )
root = v;
else if( u == u->p->left )
u->p->left = v;
else
u->p ->right = v;
v->p = u->p;
}
删除函数
红黑树的删除一共有4*2=8种情况,左右对称各四种。

void rb_delete(Node *z)
{
Node *y = z;
bool delcol = y->color;
Node *x = z;
if(z->left == nil)
{
x = z->right;
rb_transplant(z, z->right);
}
else if(z->right == nil)
{
x = z->left;
rb_transplant(z, z->left);
}
else
{
y = find_min(z->right);
delcol = y->color;
x = y->right;
if(y->p == z)
{
x->p = y;
}
else
{
rb_transplant(y, y->right);
y->right = z->right;
y->right->p = y;
}
rb_transplant(z, y);
y->left = z->left;
y->left->p = y;
y->color = z->color;
}
if(delcol == BLACK)
rb_delete_fixup(x);
}
修复函数
void rb_delete_fixup(Node *x)
{
while(x != root && x->color == BLACK)
{
if( x == x->p->left )
{
Node *w = x->p->right;
if( w->color == RED ) //A: CASE 1
{
w->color = BLACK;
x->p->color = RED;
left_rotate(x->p);
w = x->p->right;
}
if(w->left->color == BLACK and w->right->color == BLACK) //A: CASE 2
{
w->color = RED;
x = x->p;
}
else
{
if(w->right->color == BLACK ) //A: CASE 3
{
w->left->color = BLACK;
w->color = RED;
right_rotate(w);
w = x->p->right;
}
w->color = x->p->color; //A: CASE 4
x->p->color = BLACK;
w->right->color = BLACK;
left_rotate(x->p);
x = root;
}
}
else
{
Node *w = x->p->left;
if(w->color == RED) //B: CASE 1
{
w->color = BLACK;
x->p->color = RED;
right_rotate(x->p);
w = x->p->left;
}
if(w->right->color==BLACK && w->left->color==RED) //B: CASE 2
{
w->color = RED;
x = x->p;
}
else
{
if(w->left->color == BLACK) //B: CASE 3
{
w->right->color = BLACK;
w->color = RED;
left_rotate(w);
w = x->p->left;
}
w->color = x->p->color; //B: CASE 4
x->p->color = BLACK;
w->left->color = BLACK;
right_rotate(x->p);
x = root;
}
}
}
x->color = BLACK;
}
RB-Tree全部代码
#include 输入
8
4 7 6 9 8 1 2 3
运行结果
in:
1 1
2 0
3 0
4 1
6 1
7 0
8 1
9 0
pre:
6 1
2 0
1 1
4 1
3 0
8 1
7 0
9 0
delete: 8
in:
1 1
2 0
3 0
4 1
6 1
7 0
9 1
pre:
6 1
2 0
1 1
4 1
3 0
9 1
7 0
参考文献
[1]. Cormen, Thomas H. , et al. Introduction to Algorithms, Third Edition, 308~337. The MIT Press, 2009.