树链剖分代码(洛谷3384)

题目链接

题意：树链剖分模板题　（树链剖分＋线段树）

---

准备工作:

第一步: 定义声明

// 链式前向星存图 (**** 记得开２倍空间　****)
struct EDGE
{
    int to;
    int next;
}edge[MAXX<<1];

// 线段树结构体,存和、lazy标记　(**** 记得开４倍空间 ****)
struct NODE
{
    int mark;
    int sum;
}no[MAXX << 2];

int head[MAXX<<1],a[MAXX]; 

int pre[MAXX],deep[MAXX],sz[MAXX],son[MAXX];

int top[MAXX],id[MAXX],rk[MAXX];
// 以上是用到的数组,下面代码中有解释

// 加边
void add(int be,int en,int i)
{
    edge[i].to = en;
    edge[i].next = head[be];
    head[be] = i;
}

第二步:    DFS1(int u,int fa,int dp)

u代表当前结点

fa代表当前节点的父亲节点

dp代表当前节点的深度

需要完成的工作：

• 标记每个点的深度 deep[]
• 标记每个点的父亲 pre[]
• 标记每个非叶子节点的子树大小(含它自己) sz[]
• 标记每个非叶子节点的重儿子 son[]

void DFS1(int u,int fa,int dp)
{
    pre[u] = fa;  　// 父亲节点
    deep[u] = dp;　 // 深度
    sz[u] = 1;     // 每个结点的子树大小起初都为1,包括自己
    int maxx = -1;
    for(int i=head[u]; i!=-1; i=edge[i].next)
    {
        int v = edge[i].to;  // 与u相连边的终点
        if(v == fa)　　　　　　// 这里需要判断一下,因为一开始是从 fa - u 过来的
            continue;
        DFS1(v,u,dp+1);　　　 // u的子树是v，是遍历v，同时ｖ的深度在ｕ的基础上加１
        sz[u] += sz[v];　　　 // u的子树大小要加上其孩子节点的子树大小
        if(sz[v] > maxx){　　// 找出重儿子
            maxx = sz[v];
            son[u] = v;
        }
    }
}

第三步:    DFS2(int u,int tp)

u代表当前结点

tp代表当前结点所在链的顶端结点

需要完成的工作：

• 标记每个点的新编号  id[]
• 记录当前标号在树中对应的结点 rk[]
• 处理每个点所在链的顶端  top[]
• 处理每条链

顺序：先处理重儿子再处理轻儿子

// 按先重链后轻链的顺序处理树，赋上新编号
void DFS2(int u,int tp)
{
    top[u] = tp;  // 赋值顶端结点
    id[u] = cnt;　// 当前节点的新编号为 cnt
    rk[cnt++] = u;　// 编号cnt对应的结点为ｕ
    if(!son[u])　　// 没有儿子就返回
        return ;
    DFS2(son[u],tp);　　// 先搜索重儿子
    for(int i=head[u]; i!=-1; i=edge[i].next)
    {
        int v = edge[i].to;
        if(v == pre[u] || v == son[u])
            continue;
        DFS2(v,v);　// 轻儿子
    }
}

 

第四步:   Build(1,n,1)

区间 [1,n] ,起始编号 n

// 线段树区间更新的建树过程

void Build(int l,int r,int i)
{
    if(l == r){
        no[i].sum = a[rk[l]]%mod;　// 记录和
        no[i].mark = 0;　　　　　　　// lazy 标记
        return ;
    }
    int mid = (l+r) >> 1;
    Build(l,mid,i<<1);
    Build(mid+1,r,i<<1|1);
    PushUp(i);　　　　// 随时更新该点信息
}

操作过程:

1 x y z:　对 [x,y] 加z

用到树链剖分,可以利用 top[] 来加快的确定 x y 在线段树中的下标

 设所在链顶端 (top[x]) 的深度 (deep[top[x]]) 更深的那个点为x点

• ans加上 x点到x所在链顶端 (id[top[x]] - id[x] ) 这一段区间的点权和
• 把x跳到x所在链顶端的那个点的上面一个点

不停执行这两个步骤，直到两个点处于一条链上，这时再加上此时两个点的区间和即可

这时我们注意到，我们所要处理的所有区间均为连续编号(新编号)，于是想到线段树，用线段树处理连续编号区间和

// 线段树的更新操作
void Update(int l,int r,int i,int ll,int rr,int w)
{
    if(ll <= l && r <= rr){
        no[i].mark = (no[i].mark%mod + w%mod)%mod;
        no[i].sum = (no[i].sum%mod + (w%mod*((r-l+1)%mod)%mod))%mod;
        return ;
    }
    int mid = (l+r) >> 1;
    PushDown(i,mid-l+1,r-mid);　 // 下放延迟标记
    if(ll <= mid)
        Update(l,mid,i<<1,ll,rr,w);
    if(rr > mid)
        Update(mid+1,r,i<<1|1,ll,rr,w);
    PushUp(i);　　// 更新该点信息
}


void Rupdate(int x,int y,int w)
{
    while(top[x] != top[y]){  　　 // 如果两个不是在同一条链上
        int dp1 = deep[top[x]];　　// 求两个顶端链的深度
        int dp2 = deep[top[y]];

　　　　 // 　△
        if(dp1 >= dp2){　 // 如果x的顶端链的深度更大，则求 [x,top[x] ] 这一段区间的和
            Update(1,n,1,id[top[x]],id[x],w);　// id[top[x]] < id[x]
            x = pre[top[x]];              // x跳到顶端链的父亲节点处
        } 

        else {　　　// 如果ｙ的顶端链深度更大，进行类似的操作
            Update(1,n,1,id[top[y]],id[y],w);
            y = pre[top[y]];
        }
    }

　　// 虽然两个位于同一条链,但不一定是同一个点,还需要加上这一段区间的和
   // 区间从编号小的开始
    if(id[x] <= id[y])
        Update(1,n,1,id[x],id[y],w);
    else
        Update(1,n,1,id[y],id[x],w);
}

/*
if(num == 1) 
    Rupdate(be,en,c);
*/

 

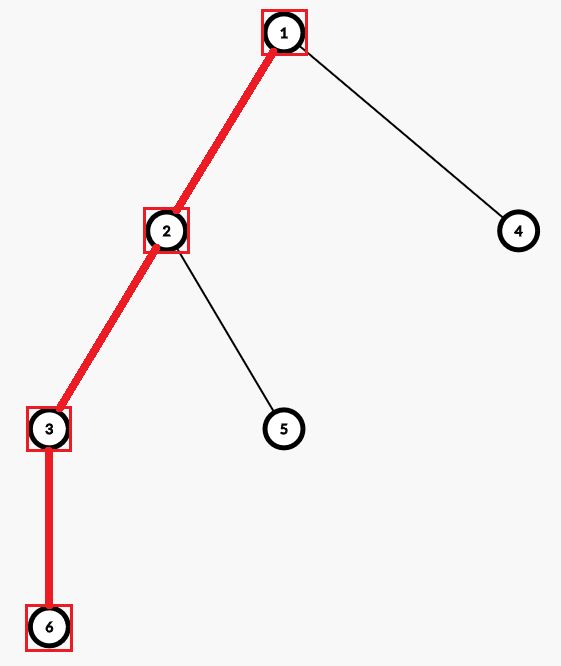
例如：

如果我们要处理从节点6到节点5的操作，会发现节点5所在链的顶端正好与节点6所在链的中间相连。

如果我们不加上△处，很可能就会跳到其它无关紧要的节点上，并且陷入死循环

△处，这句话就是为了处理当x,y跳到了同一条链上的时候该如何处理

①:　Update 5这一点( id[top[5]] = 5, id[5] = 5,top[5] = 5),　５跳到结点２处

②：发现在同一条链上，处理[2,6] 之间

 

2 x y : 输出 x 到 y 路径上的和

原理与区间修改类似

// 线段树的区间查询

int Query(int l,int r,int i,int ll,int rr)
{
    int flag = 0;
    int ans = 0;
    if(ll <= l && r <= rr){
        return no[i].sum%mod;
    }

    int mid = (l+r) >> 1;
    PushDown(i,mid-l+1,r-mid);　

    if(ll <= mid){
        flag = Query(l,mid,i<<1,ll,rr);　// 本题需要取模
        ans = (ans%mod + flag%mod)%mod;
        if(ans < 0) ans += mod;
    }
    if(rr > mid){
        flag = Query(mid+1,r,i<<1|1,ll,rr);
        ans = (ans%mod + flag%mod)%mod;
        if(ans < 0) ans += mod;
    }
    ans %= mod;
    if(ans < 0) ans += mod;
    return ans;

}

// 确定 x,y的下表
int Rquery(int x,int y)
{
    int ans = 0;
    int flag = 0;
　　
    // 以下过程与区间更新类似
    while(top[x] != top[y]){
        int dp1 = deep[top[x]];
        int dp2 = deep[top[y]];

        if(dp1 >= dp2){
            flag = Query(1,n,1,id[top[x]],id[x]);
            ans = (ans%mod + flag%mod)%mod;
            if(ans < 0) ans += mod;
            x = pre[top[x]];
        } else {
            flag = Query(1,n,1,id[top[y]],id[y]);
            ans = (ans%mod + flag%mod)%mod;
            if(ans < 0) ans += mod;
            y = pre[top[y]];
        }
    }

    flag = 0;
    if(id[x] <= id[y]){
        flag = Query(1,n,1,id[x],id[y]);
        ans = (ans%mod + flag%mod)%mod;
        if(ans < 0) ans += mod;
    } else{
        flag = Query(1,n,1,id[y],id[x]);
        ans = (ans%mod + flag%mod)%mod;
        if(ans < 0) ans += mod;
    }
    return ans;
}

3 x z : 以 x 为根节点的子树都加上 z 

我们可以知道ｘ的下标,ｘ的所有子树大小为 sz[x]

在 DFS2 中，每个子树的新编号都是连续的，可以直接用线段树查询

则我们可以确定查询的区间 [ id[x] , id[x] + sz[x] - 1 ]

Update(1,n,1,id[be],id[be]+sz[be]-1,c);

4 x  : 输出以ｘ为根节点的所有子树和

原理类似于上一部分

Query(1,n,1,id[be],id[be]+sz[be]-1);

 

完整代码：

题目链接

题意：树链剖分模板题　（树链剖分＋线段树）

// luogu-judger-enable-o2
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include