动态数组（vector）-详解均摊复杂度分析和避免避免复杂度的震荡（C++实现）
（1）首先我们先写出MyVector类的基本框架
template
class MyVector{
private:
T* data;
int size; // 存储数组中的元素个数
int capacity; // 存储数组中可以容纳的最大的元素个数
public:
MyVector(){
data = new T[100];
size = 0;
capacity = 100;
}
~MyVector(){
delete[] data;
}
} （2）为数组中添加一个元素
void push_back(T e){
assert( size < capacity );
data[size++] = e;
}
（3）从数组中拿出一个元素
// 平均复杂度为 O(1)
T pop_back(){
assert(size > 0);
size --;
return data[size];
}
以上便实现了一个静态数组，接下来，我们修改一下代码，实现动态数组
（4）当添加元素的时候，将数组的容量扩容，扩容的大小为原来的两倍
// 平均复杂度为 O(1)
void push_back(T e){
if( size == capacity )
resize( 2* capacity );
data[size++] = e;
}这首扩容不可以是一个定值，应该选择它的最小倍，即2 *容量
（5）实现调整大小（）函数
// 复杂度为 O(n)
void resize(int newCapacity){
assert(newCapacity >= size);//新添加的容量应该能够完全容纳现有的容量
T *newData = new T[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
delete[] data;
data = newData;
capacity = newCapacity;
}
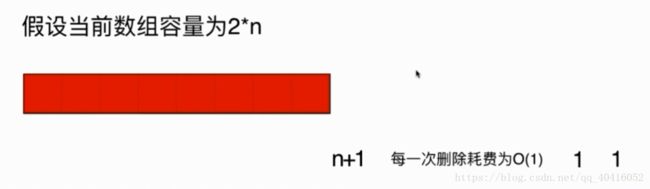
在pop_back函数中是不是也可以用同样的方法缩容呢？答案是否定的，这时候涉及到均摊复杂度分析
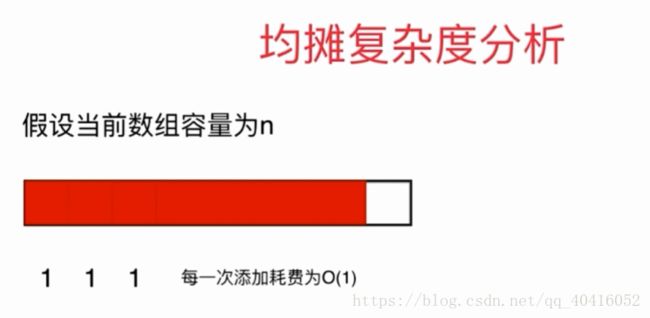
这时候再添加两个元素，数组就会扩容，然后将现有数组拷贝，需要复杂度Ñ
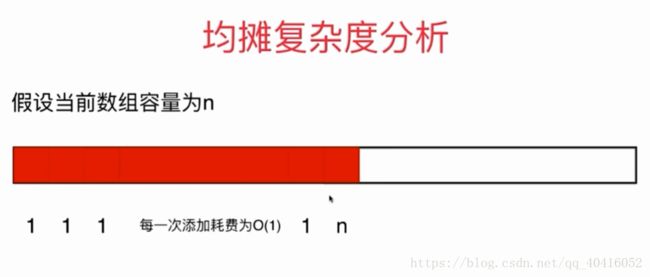前Ñ次添加元素需要耗费N，当在1/2容量出在添加一次元素需要耗费N，总共花费2
在pushback（）函数中，只有大小== capacity时，才会触发resize（），这时候将每次扩容时候所耗费的时间均匀到为调用resize（）的时间中，这便是均摊复杂度。
所以oush_back平均复杂度是O（1）。
这时候可以做一个实验，验证我们的想法。
（6）的的push_back复杂度的验证
#include
#include
#include
#include
#include "MyVector.h"
using namespace std;
int main() {
for (int i = 10; i <= 26; i++) {
int n = pow(2, i);
clock_t startTime = clock();
MyVector vec;
for (int num = 0; num < n; num++)
vec.push_back(i);
clock_t endTime = clock();
cout << 2 * n << " operations: \t";
cout << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
}
system("pause");
return 0;
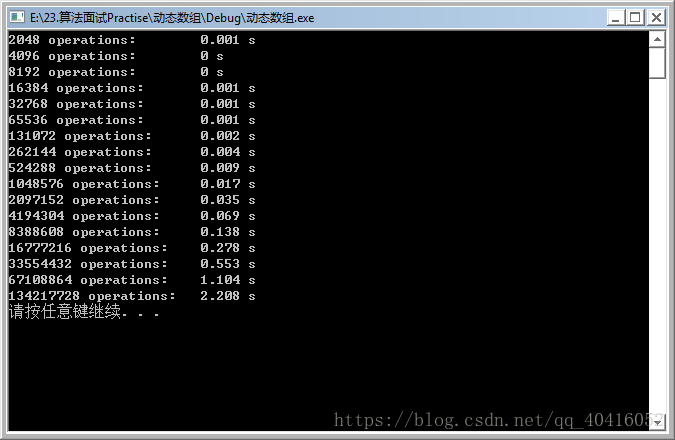
} 运行程序：
可以看到，后一个是前一个的两倍
（7）关于pop_back（），却需要做一下修改
按照添加一个元素的扩容方法，可能我们会这么做：
T pop_back(){
assert(size > 0);
size --;
if(size == capacity / 2)
resize(capacity / 2);
return data[size];
}第一点：这时候代码有一个小的错误，当size--后，缩容之后，数据[大小]这个元素已经被抹掉，这时候应该先保存：
// 平均复杂度为 O(1)
T pop_back(){
assert(size > 0);
T ret = data[size-1];
size --;
if(size == capacity / 2)
resize(capacity / 2);
return ret;
}第二点：会发生复杂度震荡：
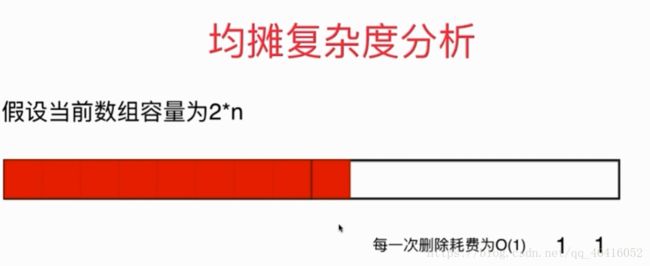
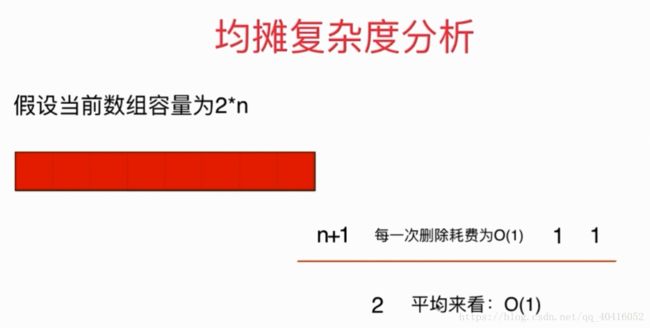
（1）每删除一个元素的复杂度为O（1）
（2）当元素只剩下Ñ个是，需要进行一次的调整大小操作
（3）调整操作：
（4）此时，时间复杂度为n + 1个，其中1为调整大小操作需花费的时间
（5）做均摊分析，可知此时平均复杂度为O（1）。
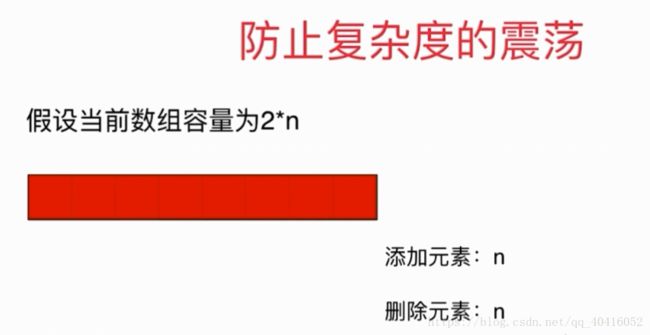
（6）此时，如果在这个临界点发生添加和删除震荡，无法均摊...
复杂度变为0（n）的
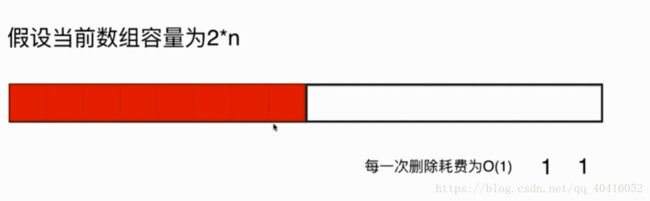
（7）所以，应该在容量为1/4的时候才进行大小调整
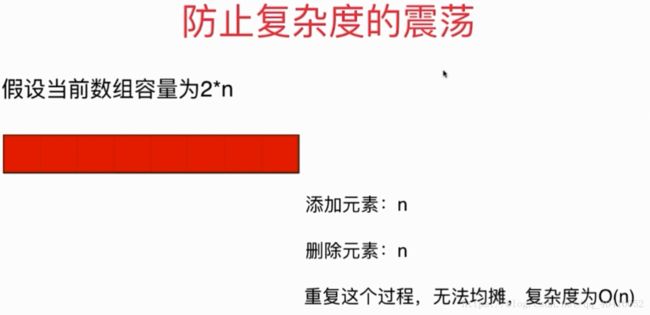
（8）此时，如果添加一个元素，需要调整大小，时间复杂度为n;
若有删除一个元素，此时容量为n，又会发生一次resize，时间复杂度为n，
这时候为再添加一个元素时，留出了空间：
（9）这时候，只需稍微修改一下代码：
// 平均复杂度为 O(1)
T pop_back(){
assert(size > 0);
T ret = data[size-1];
size --;
// 在size达到静态数组最大容量的1/4时才进行resize
// resize的容量是当前最大容量的1/2
// 防止复杂度的震荡
if(size == capacity / 4)
resize(capacity / 2);
return ret;
}（10） 到这里，我们就完成了一个动态数组的类。
以下是类的完整实现：
template
class MyVector{
private:
T* data;
int size; // 存储数组中的元素个数
int capacity; // 存储数组中可以容纳的最大的元素个数
// 复杂度为 O(n)
void resize(int newCapacity){
assert(newCapacity >= size);//新添加的容量应该能够完全容纳现有的容量
T *newData = new T[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
delete[] data;
data = newData;
capacity = newCapacity;
}
public:
MyVector(){
data = new T[100];
size = 0;
capacity = 100;
}
~MyVector(){
delete[] data;
}
// 平均复杂度为 O(1)
void push_back(T e){
if( size == capacity )
resize( 2* capacity );
data[size++] = e;
}
// 平均复杂度为 O(1)
T pop_back(){
assert(size > 0);
T ret = data[size-1];
size --;
// 在size达到静态数组最大容量的1/4时才进行resize
// resize的容量是当前最大容量的1/2
// 防止复杂度的震荡
if(size == capacity / 4)
resize(capacity / 2);
return ret;
}
};
参考资料：
https://coding.imooc.com/class/chapter/82.html#Anchor