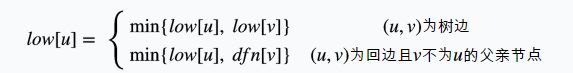求解有向图的强连通分量的SCC问题---POJ 2186 Popular Cows
【SCC问题】
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected),如果有向图G的每两个顶点都强连通,称G是一个强连通图.通俗的说法是:从图G内任意一个点出发,存在通向图G内任意一点的的一条路径.
非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components,SCC).
求图强连通分量的意义是:由于强连通分量内部的节点性质相同,可以将一个强连通分量内的节点缩成一个点(重要思想),即消除了环,这样,原图就变成了一个有向无环图(directed acyclic graph,DAG).显然对于一个无向图,求强连通分量没有什么意义,连通即为强连通.
【求解算法】
求解有向图强连通分量主要有3 个算法:Tarjan 算法、Kosaraju 算法和Gabow 算法,本文主要介绍Tarjan算法和Kosaraju算法的思想和实现过程。
1.Tarjan算法
0)预备知识
在介绍算法之前,先介绍几个基本概念。
DFS搜索树:用DFS对图进行遍历时,按照遍历次序的不同,我们可以得到一棵DFS搜索树,如图(b)所示。
树边:(又称为父子边),在搜索树中的实线所示,可理解为在DFS过程中访问未访问节点时所经过的边。
回边:(又称为返祖边、后向边),在搜索树中的虚线所示,可理解为在DFS过程中遇到已访问节点时所经过的边。
我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小),那么low[u]的计算过程如下:
1)基本原理
Tarjan 算法是基于DFS 算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。当dfn(u)=low(u)时,以u 为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下:
algorithm tarjan is
input: 图 G = (V, E)
output: 以所在的强连通分量划分的顶点集
index := 0
S := empty // 置栈为空
for each v in V do
if (v.index is undefined)
strongconnect(v)
end if
function strongconnect(v)
// 将未使用的最小index值作为结点v的index
v.index := index
v.lowlink := index
index := index + 1
S.push(v)
// 考虑v的后继结点
for each (v, w) in E do
if (w.index is undefined) then
// 后继结点w未访问,递归调用
strongconnect(w)
v.lowlink := min(v.lowlink, w.lowlink)
else if (w is in S) then
// w已在栈S中,亦即在当前强连通分量中
v.lowlink := min(v.lowlink, w.index)
end if
// 若v是根则出栈,并求得一个强连通分量
if (v.lowlink = v.index) then
start a new strongly connected component
repeat
w := S.pop()
add w to current strongly connected component
until (w = v)
output the current strongly connected component
end if
end function2)算法演示
Byvoid在这里做了一个详细的介绍和演示。我搬运一下:
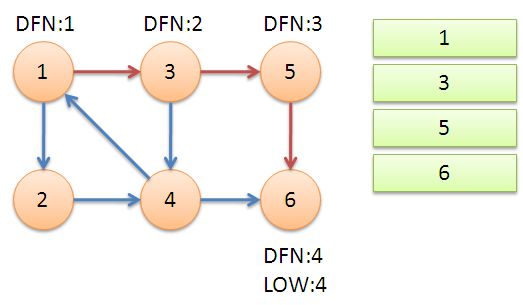
1. 从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
2. 返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
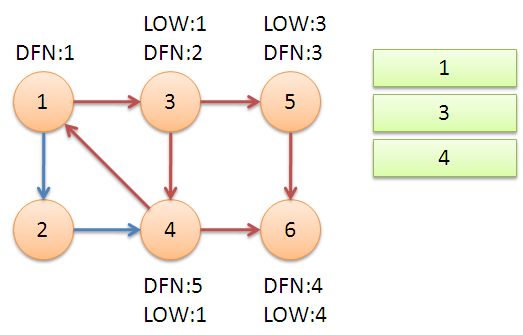
3. 返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
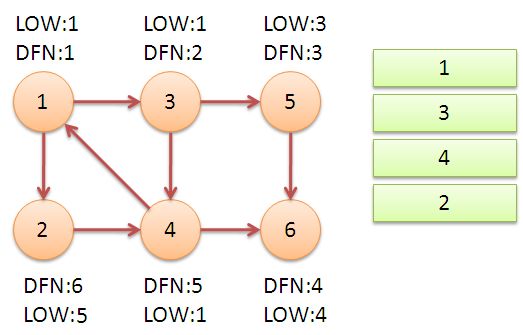
4. 继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
3)复杂度分析
运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(V+E)。
当图是使用邻接矩阵形式组建的,算法的时间复杂度为O(V^2)。
4)备注
1. 判断结点是否在栈中应在常数时间内完成,例如可以对每个结点保存一个是否在栈中的标记。
2. 同一个强连通分量内的结点是无序的,但此算法具有如下性质:每个强连通分量都是在它的所有后继强连通分量被求出之后求得的。因此,如果将同一强连通分量收缩为一个结点而构成一个有向无环图,这些强连通分量被求出的顺序是这一新图的拓扑序的逆。
2.Kosaraju 算法
1)基本原理
Kosaraju算法利用了有向图的这样一个性质,一个图和他的逆图transpose graph(边全部反向)具有相同的强连通分量。
Kosaraju算法的原理为:如果有向图G 的一个子图G'是强连通子图,那么各边反向后没有任何影响,G'内各顶点间仍然连通,G'仍然是强连通子图。但如果子图G'是单向连通的,那么各边反向后可能某些顶点间就不连通了,因此,各边的反向处理是对非强连通块的过滤。
算法伪代码:
Kosaraju's algorithm is simple and works as follows:
- Let G be a directed graph and S be an empty stack.
- While S does not contain all vertices:
- Choose an arbitrary vertex v not in S. Perform a depth-first search starting at v.Each time that depth-first search finishes expanding a vertex u, pushu onto S.
- Reverse the directions of all arcs to obtain the transpose graph.
- While S is nonempty:
- Pop the top vertex v from S. Perform a depth-first search starting at v. The set of visited vertices will give the strongly connected component containing v; record this and remove all these vertices from the graph G and the stack S. Equivalently,breadth-first search (BFS) can be used instead of depth-first search.
2)复杂度分析
当图是使用邻接表形式组建的,Kosaraju算法需要对整张图进行了两次的完整的访问,每次访问与顶点数V和边数 E之和 V+E成正比,所以可以在线性时间O(V+E)内访问完成。该算法在实际操作中要比Tarjan算法要慢,Tarjan算法只需要对图进行一次完整的访问。
当图是使用邻接矩阵形式组建的,算法的时间复杂度为O(V^2)。
3)拓扑排序
拓扑排序有两种方法,具体方法可以看这篇博客。其中一种就是基于DFS的拓扑排序。
kosaraju算法在对原图进行DFS的时候在递归返回后,Each time that depth-first search finishes expanding a vertex u, pushu onto S.实际上和使用基于DFS的拓扑排序中添加顶点到最终结果栈中的过程几乎一致,只不过,只不过这里的图不一定是DAG,而拓扑排序中的图一定是DAG。
对非有向无环图来说,是不能进行拓扑排序的,所以实际上的S栈中的的序列实际上是“伪拓扑排序”,因为最终的结果不一定满足拓扑排序中严格的偏序定义,这是由于回边的存在。
而而这些回向边,就是构成强连通分量的关键。为了突出这些回向边,Kosaraju算法将图进行转置后,原来的回向边就都变成正向边了,对转置后的图按照上面”伪拓扑排序“中顶点出现的顺序调用DFS,而每次调用DFS形成的一颗搜索树,就构成了原图中的一个强连通分量。
4)备注
该算法和Tarjan算法具有相似(相反?)的性质:每个强连通分量都是在它的所有后继强连通分量被求出之前求得的。这是因为在对原图进行DFS时得到了“伪拓扑序的逆”,再对逆图进行DFS的时候是按照这个“伪拓扑序的逆”的逆进行的,所以连通分量求出顺序和原图缩点后得到新图的拓扑序一致。因此,如果将同一强连通分量收缩为一个结点而构成一个有向无环图,这些强连通分量被求出的顺序是这一新图的拓扑序。
【算法应用:POJ2186】
题意:每头奶牛都梦想着成为牧群中最受奶牛仰慕的奶牛。在牧群中,有N 头奶牛,1≤N≤10,000,给定M 对(1≤M≤50,000)有序对(A, B),表示A 仰慕B。由于仰慕关系具有传递性,也就是说,如果A 仰慕B,B 仰慕C,则A 也仰慕C,即使在给定的M 对关系中并没有(A, C)。你的任务是计算牧群中受每头奶牛仰慕的奶牛数量。
题解:
由于仰慕的传递性,一强连通分量内的牛都互相仰慕,并且如果一个连通分量A内的一头牛仰慕另一个连通分量B内的另一头牛,则A连通分量内的所有牛都仰慕B连通分量的所有牛。所以讲图中的连通分量缩为一个点,构造新图,则这个图为DAG。最后作一次扫描,统计出度为0 的顶点个数,如果正好为1,则说明该顶点(是一个新构造的顶点,即对应一个强连通分量)能被其他所有顶点走到,即该强连通分量为所求答案,输出它的顶点个数即可。
代码1:(Tarjan算法)
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAX=10000+10;
vector g[MAX];//——邻接表存图
stack st;//—栈
int dfn[MAX],low[MAX],instack[MAX];//dfn——dfs访问次序,low——通过其子树能访问到的最小的dfn,instack——是否在栈中
int sccno[MAX],sccsize[MAX];//sccno——每个点强连通分量的标号,sccsize——每个强连通分量内点的个数
int out[MAX];//——强连通分量的出度
int dfs_cnt,scc_cnt;//dfs_cnt——dfs访问序号,scc_cnt——强连通分量个数
int n,m;//点数,边数
void dfs(int u)
{
dfn[u]=low[u]=++dfs_cnt;
instack[u]=1;
st.push(u);
for(int i=0;i 代码2:(Kosaraju算法)(参考:http://blog.csdn.net/whai362/article/details/46964883)
这里进行了一个改进,根据Kosaraju算法的性质(连通分量求出顺序为缩点后新图的拓扑序),Kosaraju算法完成后,拓扑排序其实也完成了,判断是否与所有连通分量都和拓扑序终点相连即可,如果是则结果为其顶点数,否则为0。
#include
#include
#include
#include
#include
using namespace std;
const int MAX=10000+10;
vector G[MAX];
vector rG[MAX];
vector vs;
int vis[MAX];
int sccno[MAX];
int scc_cnt;
int n,m;
void dfs(int u)
{
vis[u]=1;
for(int i=0;i=0;i--)
{
int v=vs[i];
if(!vis[v])
{
scc_cnt++;
rdfs(v);
}
}
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
while(scanf("%d%d",&n,&m)!=EOF)
{
for(int i=1;i<=n;i++)
{
G[i].clear();
rG[i].clear();
}
for(int i=0;i 参考资料:
1.Tarjan算法 - 维基百科,自由的百科全书
2.【图论】求无向连通图的割点
3.求解强连通分量算法之---Kosaraju算法
4.拓扑排序的原理及其实现
5.有向图强连通分量的Tarjan算法 - BYVoid
6.强连通分量分解 Kosaraju算法 (poj 2186 Popular Cows)
7.《图论算法理论、实现及应用》