LeetCode 39、40组合总和 （c++实现）

题39 组合总和

link

考察点：回溯，去重

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

• candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
[7],
[2,2,3]
]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
[2,2,2,2],
[2,3,3],
[3,5]
]

解答：

回溯就不说了，关键是去重，就要保证先排序，然后每次往下查找保证查找的范围比当前值大，就可以去重了。

灵魂是sort，和增加一个搜索开始的位置s，保证下次搜索从这里开始往后搜索。

class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        if (candidates.size() == 0) return res;
        vector<int> track;
        sort(candidates.begin(), candidates.end());
        backtrack(track, 0, candidates, target);
        return res;
    }

    void backtrack(vector<int> &track, int s, vector<int>& candidates, int target) {
        if (target == 0) {
            res.push_back(track);
            return ;
        }
        for (int i = s; i < candidates.size(); i++) {
            if (candidates[i] > target) break;
            track.push_back(candidates[i]);
            backtrack(track, i, candidates, target - candidates[i]);
            track.pop_back();
        }
    }

};

题40. 组合总和二

link

考察点：回溯、去重，但这个是无放回的组合。

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

• candidates 中的每个数字在每个组合中只能使用一次。

说明：

• 所有数字（包括目标数）都是正整数。
• 解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]

示例 2:

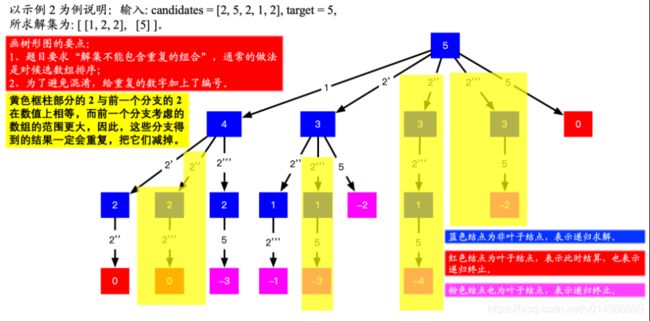
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]

解答：

这个图是灵魂，

黄色框柱部分的2与前一个分支的2相等，但前一个搜索范围更大，所以后面的都可以去掉了。

class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        if (candidates.size() == 0) return res;
        vector<int> track;
        sort(candidates.begin(), candidates.end());
        backtrack(track, 0, candidates, target);
        return res;
    }

    void backtrack(vector<int> &track, int s, vector<int>& candidates, int target) {
        if (target == 0) {
            res.push_back(track);
            return ;
        }
        for (int i = s; i < candidates.size(); i++) {
            if (candidates[i] > target) break;
            if(i > s && candidates[i] == candidates[i-1]) continue; // 增加了这一行，去重
            track.push_back(candidates[i]);
            backtrack(track, i+1,/*更改了这里*/ candidates, target - candidates[i]);
            track.pop_back();
        }
    }

};