九度 1095:2的幂次方
题目描述:
Every positive number can be presented by the exponential form.For example, 137 = 2^7 + 2^3 + 2^0。
Let's present a^b by the form a(b).Then 137 is presented by 2(7)+2(3)+2(0). Since 7 = 2^2 + 2 + 2^0 and 3 = 2 + 2^0 , 137 is finally presented by 2(2(2)+2 +2(0))+2(2+2(0))+2(0).
Given a positive number n,your task is to present n with the exponential form which only contains the digits 0 and 2.
思路
1. 蛮有意思的一道题, 拿来联系递归函数很好使
2. 题目的核心是递归函数, 而递归函数的核心又是退出条件. 从 137 这个案例可以看出, 当输入是 2 时, 返回 2 , 输入为 1 时返回 2(0). 起初, 我以为 2 的返回应该是 2(2(0)). 这就可以看出, 当 n = 2 时就已经需要退出了, n = 1 时, 自然更要退出了
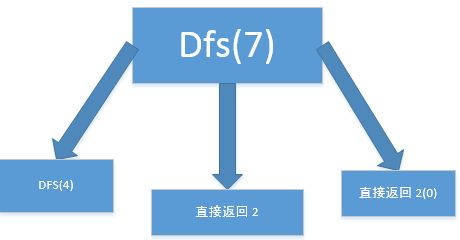
3. 括号和加号的处理, 括号在父 DFS 加上(n==1 时例外), 加号由子DFS函数给出, 当 n = 0 时, 没有后续了, 就不用加号
4. 退出条件的位置. 一般来讲, 退出条件要放在 DFS 的上部分, 但这道题放在下面比较合适, 比如当 n = 3 时, 要写成 2 + 2(0)
代码
#include <iostream> #include <stdio.h> #include <string> #include <cstring> using namespace std; int pow2[20]; void init() { pow2[0] = 1; for(int i = 1; i < 18; i ++) { pow2[i] = 2 * pow2[i-1]; } } void dfs(int n, string &party) { for(int i = 16; i > 1; i --) { if(n >= pow2[i]) { party.push_back('2'); party.push_back('('); dfs(i, party); party.push_back(')'); n = n - pow2[i]; if(n != 0) party.push_back('+'); } } if(n >= 2) { party.push_back('2'); n = n -2; if(n != 0) party.push_back('+'); } if(n != 0) { party.append("2(0)"); n = 0; } } int n; int main() { freopen("testcase.txt", "r", stdin); init(); while(scanf("%d", &n) != EOF) { string str; dfs(n, str); cout << str << endl; } return 0; }