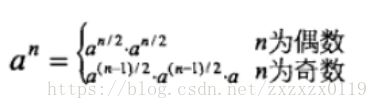乘法快速幂相关总结 & LeetCode - 50. Pow(x, n)
乘法快速幂相关总结 & LeetCode - 50. Pow(x, n)
- 递归计算 (a n) % mod
- 非递归计算 (a n) % mod
- 计算 ( a * b ) % mod
- 配合 ( a * b ) % mod和乘法快速幂
- XYNUOJ - 1872. 次方求模题解
- LeetCode - 50. Pow(x, n)题解
递归计算 (a n) % mod
递归计算其实是更容易理解的:
- 为了求an，我们先递归去求出an/2，得到结果记录为
halfRes； - 然后如果
n为偶数，很好办，再乘以一个halfRes就可以了(再取模一下)，也就是可以返回halfRes*halfRes； - 但是如果
n为奇数的话，就需要再乘以一个a，然后再返回；
static long pow_mod(long a, long n, long mod) {
if (n == 0) // a^0 = 1
return 1;
// 先求一半的 --> 你先给我求出 a ^ (n/2) 的结果给我
long halfRes = pow_mod(a, n >> 1, mod); // n >> 1 --> n/2
long res = halfRes * halfRes % mod;
if ((n & 1) != 0) // odd num
res = res * a % mod;
return res;
}
非递归计算 (a n) % mod
假设一个整数是10，如何最快的求解10的75次方。
- ①
75的二进制形式为1001011； - ②
10的75次方 = 1064 × 108 × 102 × 101； - 在这个过程中，我们先求出101，然后根据101求出102，再根据102求出104。。。。，最后根据1032求出1064，即
75的二进制数形式总共有多少位，我们就使用了多少次乘法； - ③ 在步骤②进行的过程中，把应该累乘的值相乘即可，比如1064、108、102、101应该累乘，因为
64、8、2、1对应到75的二进制数中，相应位上是1；而1032、1016、104不应该累乘，因为32、16、 4对应到75的二进制数中，相应位是0；
static long pow_mod2(long a, long n, long mod) {
long res = 1;
while (n > 0) {
if ((n & 1) != 0) // 二进制最低位 是 1 --> (n&1) != 0 --> 乘上 x ^ (2^i) (i从0开始)
res = res * a % mod;
a = a * a % mod; // a = a^2
n >>= 1; // n -> n/2 往右边移一位
}
return res;
}
使用a ^ 11来模拟一下计算过程:
计算 ( a * b ) % mod
// 计算 (a * b) % mod
static long mul_mod(long a, long b, long mod){
long res = 0;
while(b > 0){
if( (b&1) != 0) // 二进制最低位是1 --> 加上 a的 2^i 倍, 快速幂是乘上a的2^i ）
res = ( res + a) % mod;
a = (a << 1) % mod; // a = a * 2 a随着b中二进制位数而扩大 每次 扩大两倍。
b >>= 1; // b -> b/2 右移 去掉最后一位 因为当前最后一位我们用完了，
}
return res;
}
配合 ( a * b ) % mod和乘法快速幂
可以使用非递归的乘法快速幂和上面的(a*b) % mod 来计算快速幂，差别不大:
// 计算 (a * b) % mod
static long mul_mod(long a,long b,long mod){
long res = 0;
while(b > 0){
if( (b&1) != 0) // 二进制最低位是1 --> 加上 a的 2^i 倍, 快速幂是乘上a的2^i ）
res = ( res + a) % mod;
a = (a << 1) % mod; // a = a * 2 a随着b中二进制位数而扩大 每次 扩大两倍。
b >>= 1; // b -> b/2 右移 去掉最后一位 因为当前最后一位我们用完了，
}
return res;
}
//非递归 计算 (a^n) % mod 配合 mul
static long pow_mod3(long a,long n,long mod){
long res = 1;
while(n > 0) {
if( (n&1) != 0 ) // 二进制最低位 是 1 --> (n&1) != 0 --> 乘上 x ^ (2^i) (i从0开始)
res = mul_mod(res,a,mod) % mod;
a = mul_mod(a,a,mod) % mod; // a = a^2
n >>= 1; // n -> n/2 往右边移一位
}
return res;
}
XYNUOJ - 1872. 次方求模题解
题目链接
题目
完全的模板题，三种方法都可以通过:
import java.io.BufferedInputStream;
import java.util.Scanner;
/**
* 题目链接: http://xyoj.xynu.edu.cn/problem.php?id=1872&csrf=mmofuzhUWGip3c6WlmhiFY6bLxeVHZta
*/
public class Main { //提交时改成Main
//递归 计算 (a^n) % mod
static long pow_mod(long a,long n,long mod){
if(n == 0) // a^0 = 1
return 1;
// 先求一半的 --> 你先给我求出 a ^ (n/2) 的结果给我
long halfRes = pow_mod(a, n >> 1, mod); // n >> 1 --> n/2
long res = halfRes * halfRes % mod;
if( (n&1) != 0) // odd num
res = res * a % mod;
return res;
}
//非递归 计算 (a^n) % mod
static long pow_mod2(long a,long n,long mod){
long res = 1;
while(n > 0) {
if( (n&1) != 0 ) // 二进制最低位 是 1 --> (n&1) != 0 --> 乘上 x ^ (2^i) (i从0开始)
res = res * a % mod;
a = a * a % mod; // a = a^2
n >>= 1; // n -> n/2 往右边移一位
}
return res;
}
// 计算 (a * b) % mod
static long mul_mod(long a,long b,long mod){
long res = 0;
while(b > 0){
if( (b&1) != 0) // 二进制最低位是1 --> 加上 a的 2^i 倍, 快速幂是乘上a的2^i ）
res = ( res + a) % mod;
a = (a << 1) % mod; // a = a * 2 a随着b中二进制位数而扩大 每次 扩大两倍。
b >>= 1; // b -> b/2 右移 去掉最后一位 因为当前最后一位我们用完了，
}
return res;
}
//非递归 计算 (a^n) % mod 配合 mul
static long pow_mod3(long a,long n,long mod){
long res = 1;
while(n > 0) {
if( (n&1) != 0 ) // 二进制最低位 是 1 --> (n&1) != 0 --> 乘上 x ^ (2^i) (i从0开始)
res = mul_mod(res,a,mod) % mod;
a = mul_mod(a,a,mod) % mod; // a = a^2
n >>= 1; // n -> n/2 往右边移一位
}
return res;
}
public static void main(String[] args) {
Scanner cin = new Scanner(new BufferedInputStream(System.in));
int T = cin.nextInt();
while(T-- > 0){
int a = cin.nextInt();
int n = cin.nextInt();
int mod = cin.nextInt();
// System.out.println(pow_mod(a,n,mod));
// System.out.println(pow_mod2(a,n,mod));
System.out.println(pow_mod3(a,n,mod));
}
}
}
LeetCode - 50. Pow(x, n)题解
题目链接
题目
解析
这个题目和普通的求幂不同的是:
- 其中
x(底数)是double类型的，且n是范围是Integer范围的(可正可负) : - 要注意的就是当
n为负数的时候，我们可以转换成求1.0 / pow(x,-n)； - 还一个很重要的地方就是当
n = Integer.MIN_VALUE的时候要特殊处理，因为整形范围是 − 2 31 到 2 31 − 1 -2^{31} 到 2^{31} - 1 −231到231−1 所以或者我们使用long来存转换的数，或者特殊判断一下；
递归求解:
两种写法意思一样，第二种写法更加简洁:
class Solution {
public double myPow(double x, int n) {
if (n > 0) {
return pow(x, n);
} else {
if (n == Integer.MIN_VALUE) {
return 1.0 / (pow(x, -(Integer.MIN_VALUE + 1)) * x); // MAX_VALUE = -(Integer.MIN_VALUE + 1)
}
return 1.0 / pow(x, -n);
}
}
public double pow(double x, int n) {
if (n == 0)
return 1;
double half = pow(x, n / 2);
if (n % 2 == 0)
return half * half;
else
return x * half * half;
}
}
class Solution {
public double myPow(double x, int n) {
if (n == 0)
return 1.0;
if (n < 0) {
if (n == Integer.MIN_VALUE) {
// return 1.0 / (myPow(x,-(Integer.MIN_VALUE+1)) * x);
return 1.0 / (myPow(x, Integer.MAX_VALUE) * x);
}
return 1.0 / myPow(x, -n);
}
double half = myPow(x, n / 2);
if (n % 2 == 0)
return half * half;
else
return x * half * half;
}
}
非递归求解:
三种写法的意思都是一样，只不过处理Integer.MIN_VALUE的方式不同而已。
class Solution {
public double myPow(double x, int n) {
if (n == 0)
return 1.0;
if (n < 0) {
if (n == Integer.MIN_VALUE) {
return 1.0 / (myPow(x, Integer.MAX_VALUE) * x);
} else {
return 1.0 / myPow(x, -n);
}
}
double res = 1.0;
while (n > 0) {
if ((n & 1) != 0)
res *= x;
x = x * x;
n >>= 1;
}
return res;
}
}
class Solution {
public double myPow(double x, int n) {
if (n == 0)
return 1.0;
double res = 1.0;
if (n < 0) {
x = 1 / x;
n = -(1 + n); // for Integer.MIN_VALUE
res *= x; // x is 1/x because n is -(n+1) so should do this
}
while (n > 0) {
if ((n & 1) != 0)
res *= x;
x = x * x;
n >>= 1;
}
return res;
}
}
class Solution {
public double myPow(double x, int n) {
if (n == 0)
return 1.0;
long abs = Math.abs((long) n); // also for Integer.MIN_VALUE
double res = 1.0;
while (abs > 0) {
if ((abs & 1) != 0)
res *= x;
x = x * x;
abs >>= 1;
}
if (n < 0)
return 1.0 / res;
return res;
}
}