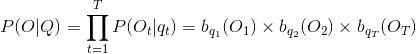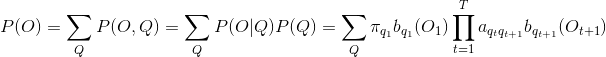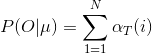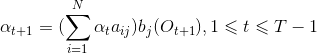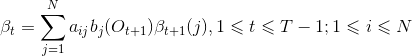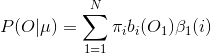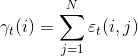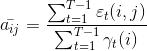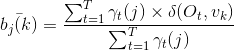隐马尔可夫模型(HMM)来龙去脉（二）
目录
前言
预备知识
一、估计问题
1、问题推导
2、前向算法/后向算法
二、序列问题
1、问题推导
2、维特比算法
三、参数估计问题
1、问题推导
2、期望最大化算法（前向后向算法）
总结
前言
HMM隐马尔可夫模型，这个名字看起来熟悉，其实很是陌生。它给人一种很神秘高深的感觉，确实，很强大的一个模型，在概率论统计学应该是应用广泛而且很重要的；虽说很高深强大的一个模型，其原理确实我们最基础的理论知识不断推导计算来的。
上一篇《原创 隐马尔可夫模型(HMM)来龙去脉（一）》，从HMM基础理论开始，我们可以学习得知，其原理来源于概率论基本重要知识，包括了条件概率、贝叶斯公式、概率分布函数...
而这一篇将继续探索隐马尔可夫模型，深入理解模型背后解决的各种问题，力求基本弄懂这个似乎熟悉而又陌生深奥的模型。接下来探索HMM三个经典的基本问题的解决方案，逐步通过问题推导，公式解析，算法实现，有章可循地真正来理解来龙去脉！
预备知识
建议先翻看前一篇《原创 隐马尔可夫模型(HMM)来龙去脉（一）》逐步详细介绍的内容。
一般的，将HMM简单表示为一个三元组
, π是初始状态的概率分布，A是状态转移概率，B是符号发射概率。
由此观察序列
可以通过以下步骤产生：
- 根据初识状态的概率分布
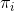选择一个初识状态
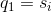. - 设t=1.
- 根据状态
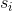的符号发射概率分布
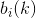输出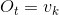
. - 根据状态转移概率分布
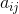，将此时 t 的状态转移到新的状态 
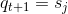. - t=t+1,如果 t
一、估计问题
1、问题推导
估计问题：给定一个观察序列
?
我们很直观知道，这其实就是一个条件概率的计算问题。在给定的模型条件下，可以推导以下：
首先根据预备知识可以计算任意状态序列Q下，观察序列O的概率：
而且 
,
另外根据条件概率
.
综上公式，求得在模型下，
.
然而，这个直观简单的推导公式，计算时间复杂度达到指数级爆炸！
! ! ! ,所以呢，需要寻找更高效的计算方法来解决指数级时间问题。
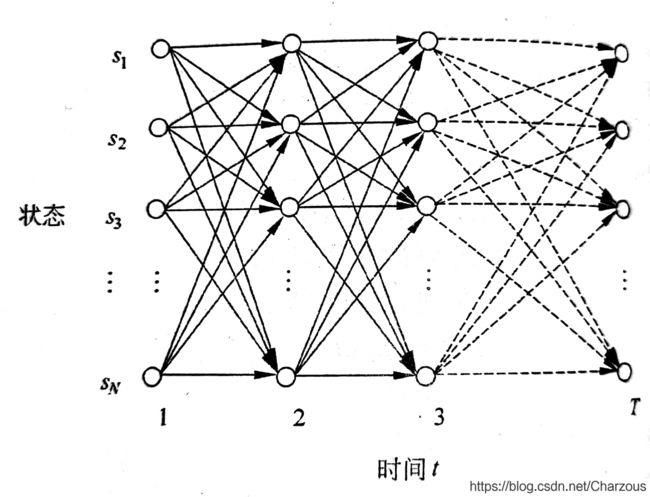
由此，引出HMM中的动态规划方法，一般用格架的组织形式描述。格架算法示意图如下：
思想是：对于一个个状态下的HMM，某一时刻结束时，每个格子能够记录HMM所有输出符号的概率，较长子路径概率可以由较短子路径概率计算出来。
2、前向算法/后向算法
第一步，定义一个前向变量
，表示在时间 t ，HMM在状态 输出一个序列的概率。
第二步，根据动态规划思想，在时间 t+1 的概率计算为：
, 其中表示从状态 i 转移到状态 j 并输出观察符号O的概率。
第三步，根据前向变量，可以计算，就是在所有状态下观察到序列O的概率：
.
前向变量归纳关系图：
前向算法总结：
1、初始化：
2、归纳计算：
3、求和：
复杂度分析：步骤1计算每个前向变量需要考虑N个状态转移，步骤2计算N个前向变量，所以时间复杂度O(N*N)，步骤3在时间1~T过程中，计算量为O(T)，所以总时间复杂度为
. 因此，使用该算法解决在多项式时间内计算问题。
后向算法方法类似，使用动态规划方法计算，后向变量定义为 
，归纳关系图如下：
后向算法总结：
1、初始化：
2、归纳计算：
3、求和：
. 同理，时间复杂度也是。
二、序列问题
1、问题推导
序列问题：给定一个观察序列
对该问题的正确理解就是，给定观察序列和模型后，使条件概率最大的状态序列，即
.
因此，维比特算法定义了一个维比特变量
. 在时间 t 时，HMM沿着某一路径到达状态 ,使观察序列O概率最大化。
.
2、维特比算法
有如下递归关系，![\delta _t(i)=max[\delta_t(j)a_{ij}]b_i(O_{t+1})](http://img.e-com-net.com/image/info8/1b50bbd43f7a4981af1f41ec9875a12c.gif){kind=small}
,根据这个递归关系，所以可以运用动态规划搜索技术。
另外，为了记录时间 t 时，HMM通过的一条概率最大的路径达到状态 ，算法设置了另外一个变量
来记录前一个时间的状态。
维比特算法如下:
三、参数估计问题
1、问题推导
参数估计问题：给定一个观察序列和模型，使得
我们知道，HMM中的状态序列是不可见的，所以这里采用期望最大化法(EM)，它可以用于含有隐变量的统计模型的参数最大似然估计。
基本思想：从
得到从某一个状态转移到另一个状态的期望次数，由此得到模型
，然后，重新估计模型的参数，执行这个迭代过程，直到参数收敛于最大似然估计值。
2、期望最大化算法（前向后向算法）
这种EM方法的具体实现使用到了前向后向算法(forward-backward algorithm)。
这里需要用到几个变量表示概率：
公式(6-24)：在时间 t 位于状态 ，时间 t+1位于状态
的概率
.
公式(6-25)：另外，在时间 t 位于状态的概率
的参数估计公式：
公式(6-26)：
公式(6-27)：
公式(6-28.)：
由上述公式，得出前向后向算法：
总结
至此，我们对隐马尔可夫模型(HMM)有了比较深入的理解，从原理上全面认识HMM实现思想，这一篇非常抽象的展示许多公式，虽然对这些公式不能够完全掌握，但是最重要的是，能够理解HMM三个基本问题解决方案的思想方法，这些经典奇妙的算法也是人们在不断探索中发现的并完善。所以，对于初学者来说，思想方法最重要，原理需要理明白，具体应用实现是利用已经封装好的工具。
这一篇将探索HMM三个经典的基本问题的解决方案，逐步通过问题推导，公式解析，算法实现，对于HMM理解不再天马行空般，来龙去脉基本理清！希望能帮助到像我一样初学者的伙伴，欢迎大佬交流指正！
两篇内容深入理解HMM：
- 隐马尔可夫模型(HMM)来龙去脉（一）
- 隐马尔可夫模型(HMM)来龙去脉（二）
我的CSDN博客：https://blog.csdn.net/Charzous/article/details/108311177
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Charzous/article/details/108311177