关于2019高压油管网格搜索可视化Python作图

网格搜索

网格搜索，通过在一张网内对$x,y$离散搜索，可以得出关于目标函数在每一个$x,y$散点的值，做可视化的时候我想到了山峰的三维表面图。

一个简单的事例

已知$x$的范围，$y$的范围，还有对应每一个$x,y$的高程数据$z$，我们就可以利用python作图。

x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 2, 3])
z = np.array([[122, 424, 221, 231, 742],
[231, 421, 423, 523, 215],
[213, 124, 231, 422, 633],
[151, 532, 241, 734, 215]])

import matplotlib.pyplot as plt
import numpy as np

x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 2, 3])
z = np.array([[122, 424, 221, 231, 742],
              [231, 421, 423, 523, 215],
              [213, 124, 231, 422, 633],
              [151, 532, 241, 734, 215]])

plt.figure()
ax = plt.axes(projection='3d')
X, Y = np.meshgrid(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_ylabel('z')
ax.plot_surface(X, Y, z, cmap='afmhot')
plt.show()

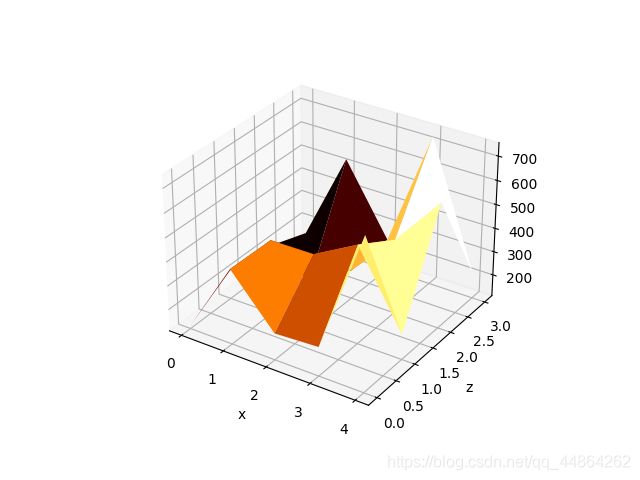
数据纯属胡编乱造，怎么样，是不是很有趣。在这个示例代码中，$x,y$的值我是从0开始设置的，步长为$1$，也就是正好对应着$z$的下标，但在实际应用过程中，$x$,$y$并不是从$1$开始的，而且$z$也一般是通过$x$,$y$确定的，所以需要用嵌套for循环，再设置两个下标变量，解决实际应用问题，请看以下代码。

关于高压油管此题的搜索可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math

data = '附件3-弹性模量与压力.xlsx'
data = pd.read_excel('附件3-弹性模量与压力.xlsx')  # 导入附件3数据
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

x_pandas_list = data[u'燃油密度(mm3/ms)']  # 附件3 燃油密度列数据
y_pandas_list = data[u'压力(MPa)']  # 附件3 压力列数据

coefficient1_numpy_list = np.polyfit(x_pandas_list, y_pandas_list,
                                     2)  # [ 10784.65349198 -15693.86029255   5648.09019803]y=压强 x=密度拟合系数


def ρ_P(x):  # 密度转压力函数
    return coefficient1_numpy_list[0] * x ** 2 + coefficient1_numpy_list[1] * x + coefficient1_numpy_list[2]


coefficient2_numpy_list = np.polyfit(y_pandas_list, x_pandas_list,
                                     2)  # [-6.59843062e-07  5.23409641e-04  8.04251284e-01]y=密度 x=压强拟合系数


def P_ρ(x):  # 压力转密度函数
    return coefficient2_numpy_list[0] * x ** 2 + coefficient2_numpy_list[1] * x + coefficient2_numpy_list[2]


C = 0.85  # 流量系数

d_a = 1.4  # 小孔处的直径1.4mm
r_a = d_a / 2  # 小孔处的半径1.4mm
A = S_a = math.pi * r_a ** 2  # 小孔处的面积1.5393804002589984mm2

l_primary = 500  # 内腔长度500mm
d_primary = 10  # 内腔直径10mm
r_primary = d_primary / 2  # 内腔半径5mm
S_primary = math.pi * r_primary ** 2  # 内腔横截面积78.53981633974483mm2
V_primary = S_primary * l_primary  # 内腔体积39269.90816987242mm3

ρ0 = 0.85  # 初始100MPa压力下的密度
ρ160 = P_ρ(160)  # 160MPa压力下的密度 0.8711048440368855mg/mm3
m0 = ρ0 * V_primary  # 初始高压油管油气33379.42194439156mg

t = 0  # 记录时刻
t_ = 0.1  # 每隔0.01ms时间段刷新一次状态
m = m0  # 记录每一时刻高压油管内的质量 初始为m0
P = 100  # 记录每一时刻高压油管内的压强
ρ = 0.85  # 录每一时刻高压油管内的密度
P_list = []  # 压强时刻表


# 进油函数 参数t为时刻，t1为进油时间段
def enter(t, t1):
    global m, P, ρ  # 全局变量，可做修改
    if 0 < t % (t1 + 10) < t1:
        Q = C * A * math.sqrt(2 * (160 - P) / ρ160)  # 单位时间进油量
        det_m = Q * ρ160 * t_  # 0.01为步长 质量改变量
        m = m + det_m  # 更新质量
        rou = m / V_primary  # 更新密度
        P = ρ_P(rou)  # 更新压强
    else:
        pass


# 出油函数 参数t为时刻，t0为出油时刻
def out(t, t0):
    global m, P, ρ  # 全局变量，可做修改
    if t0 < (t % 100) < t0 + 0.2:  # 第一段0~0.2ms
        Q = (t - t0) % 100 * 100  # 在不同周期内时刻的流量
        det_m = Q * ρ * t_  # 0.01为步长 质量改变量
        m = m - det_m  # 更新质量
        ρ = m / V_primary  # 更新密度
        P = ρ_P(ρ)  # 更新压强
    elif t0 + 0.2 <= (t % 100) < t0 + 2.2:  # 第二段0.2~2.2ms
        Q = 20
        det_m = Q * ρ * t_  # 0.01为步长 质量改变量
        m = m - det_m  # 更新质量
        ρ = m / V_primary  # 更新密度
        P = ρ_P(ρ)  # 更新压强
    elif t0 + 2.2 <= (t % 100) <= t0 + 2.4:  # 第三段2.2~2.4ms
        Q = ((t - t0) * (-100) + 240) % 100
        det_m = Q * ρ * t_  # 0.01为步长 质量改变量
        m = m - det_m  # 更新质量
        ρ = m / V_primary  # 更新密度
        P = ρ_P(ρ)  # 更新压强
    else:
        pass


sum_min = 10000000000000  # 刷新压力波动最小值
P_list_min = []  # 波动最小的压力差表
i_best = 0  # 最优开阀门时长
j_best = 0  # 最优出气时刻

x = np.arange(0.285, 0.29, 0.001)
y = np.arange(50, 60, 1)
z = np.zeros([len(y), len(x)])
q = -1

for i in x:  # 遍历开阀门时长 start->end
    q = q + 1
    p = -1
    for j in y:  # 遍历出气时刻 start->end
        p = p + 1
        sum = 0  # 记录压力波动偏差
        t = 0  # 每次循环刷新时刻从0开始
        P_list = []  # 每次循环刷新压力时刻表 为空表
        while t <= 5000:  # 时间可修改，单位为ms 循环2000/t_次
            t = t + t_
            enter(t, i)
            out(t, j)
            P_list.append(P)
            sum = sum + abs(P - 100)  # 每隔t_=0.01ms时刻记录一下总波动 best=sum|P-100|
            z[p][q] = sum
        print('开始遍历：', 'i =', i, 'j =', j)
        print('压差距离最优质值和（越小越好）：', sum)
        if sum_min > sum:
            sum_min = sum
            i_best = i
            j_best = j
            P_list_min = P_list

print('最优开阀门时长为：', i_best, '最优出气时刻为：', j_best)

len_P_list = len(P_list)  # 长度为设值遍历长度个
x_numpy_list = np.arange(0, len_P_list * t_, t_)  # 每隔0.01ms列一个x坐标与P_list对应

plt.figure()  # 创建一个绘图对象
ax = plt.axes(projection='3d')  # 用这个绘图对象创建一个三维坐标轴对象
X, Y = np.meshgrid(x, y)
ax.plot_surface(X, Y, z, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()