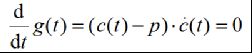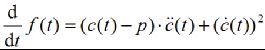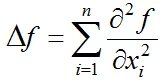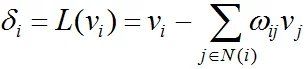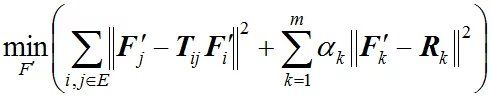chicken-and-egg problem的一些想法
这里所谓的chicken-and-egg problem,不是争论先有鸡还是先有蛋问题,而是二者互生共存问题,以彼此的存在为前提和依赖基础。要求解A,需依赖于B,而B又以A的条件为基础。这类问题在工程实践中还不少,如何解决这类问题呢?我觉得最简单也是最容易想到的就是迭代方法,这是一个基本思路;另外,就是要根据具体问题,用另外一种内在的关联性的解决来替代解决原问题的这种关联性。
关于迭代求解问题,我们先来看一段戏文(越调《收姜维》选段):
这书信你牢牢带在身上
冀城县你去搬那姜维的老娘
带人马攻冀城一路喧嚷
诱姜维出天水我另有主张
见姜母替山人把好话多讲
你就说姜伯约降顺汉王
那姜母她若肯随你前往
不用杀不用战
(白)四千岁
管叫他自来汉降。
这段戏文大家可能不熟悉,但这段故事大家如果看过《三国演义》的话,应该不会陌生。诸葛亮攻打天水城时,其计谋被天水守将姜维(字伯约)识破,从而使常胜将军赵云大败而归。赵云羞惭自责,诸葛亮主动承担责任,调整计划,派赵云去请(诱迫?)姜维的母亲,以便迫使姜维降汉。这里面就存在着 “ Chicken - and - Egg ”问题,要想使姜维降汉,需要以姜母降汉为要挟手段,而劝诱姜母降汉,也需要以姜维降汉为前提。(这里只是做一个例子,没有考虑其中的逻辑严谨性,见谅!)所以诸葛亮就采用了这种所谓的迭代求解策略,在迭代之前,需要给定一个初值,即先假定其中一个条件已经具备了,这里在劝诱姜母时即假定(诱骗姜母)姜维已经降汉,而如果一旦姜母顺利请来,则“管叫他自来汉降”,姜维降汉就容易解决了。我们知道,在迭代算法中,初值的选择也很重要,初值选择不好的话,有时迭代是发散的,比如牛顿迭代算法就对初值很敏感。在这里也一样,姜维至孝,所以选择姜母做初值,迭代容易收敛。
单纯从戏文的角度讲, 这样讲不太好,过于直白,影响孔明先生的形象,所以后来有一个版本中,把这句“你就说姜伯约降顺汉王”改为了“你就说山人我敬慕非常”,大棒变成了胡萝卜,呵呵,这是题外话。
上面的戏文例子只是想把问题说得通俗一点,不够严谨。下面举两个计算机辅助几何设计和数字几何处理方面的例子,看看在科研实践中对这类 “Chicken-and-Egg ”问题的处理策略。
(1) 点在曲线上的Footpoint(最近点)点计算
如图1所示,c(t)为参数曲线,p为任意一点,曲线上距离p点最近的点可以通过最小化如下方程获得
上式最小时的t设为t*,c(t*)即称为p点在曲线c(t)上的foot point。
图1 点在曲线上的foot point 点计算
大家知道,要使(1)式最小,即应使其满足取极值的条件:
上式的几何意义就是p点与其在曲线上的foot point 点的连线应垂直于曲线在该点的切线。即要求取foot point 点,有赖于该点的切线(一阶导数),而该点不知道的话,其切线也就无从计算,是一个典型的Chicken-and-Egg问题。我们这里采用牛顿迭代方法对其进行求解,牛顿迭代方法在任一本计算方法书中都有。
代入牛顿迭代公式有,
迭代的终止条件为 |tk+1-tk| < ε,或者p点到c(tk+1)的距离小于给定误差,或者迭代次数超过给定的最大迭代次数,其中ε为指定的误差限。
(2) 拉普拉斯坐标的旋转敏感性问题
拉普拉斯算子是 n 维欧氏空间中的一个二阶微分算子,被定义为梯度(▽f )的散度(Δf )。如果f是二阶可微的实函数,则 f 的拉普拉斯算子被定义为:
![]() 的拉普拉斯算子也就是笛卡尔坐标系下所有变量的非混合二阶偏导数,即:
的拉普拉斯算子也就是笛卡尔坐标系下所有变量的非混合二阶偏导数,即:
在曲面上的拉普拉斯坐标蕴含了曲面的局部微分几何信息,包括法矢、曲率等,因而在曲面光顺,曲面变形等领域应用甚广,特别是在网格变形领域,因其具有保细节的特性,因而国内外学者围绕其相关算法做了大量系统研究。拉普拉斯坐标具有平移不变性,但不具有旋转不变性。
给定具有n个顶点的三角网格模型M=(V,E,F),V为顶点集,E为边集,F为三角面片集合。设v1,…vn为点集V中的点,对于每个顶点vi,用传统的笛卡尔坐标表示,记vi=(xi,yi,zi);用N(i)={j|(i,j)∈E},表示第i点的1-ring邻域顶点构成的集合,如图2所示,定义vi处的拉普拉斯坐标为
式中,δi为顶点vi的拉普拉斯坐标,L(·)为网格的拉普拉斯算子,ωij为vj点相对于vi点的权值。
图2 曲面顶点的拉普拉斯坐标
对于具有n个顶点的网格模型M,求取其变形后顶点位置V',可归结为求解如下方程组:
式中,L为n×n的拉普拉斯矩阵,其秩为n-k,k是M连通子集的个数,Δ为顶点的拉普拉斯坐标矩阵。由于L是非满秩矩阵,需要至少增加k个顶点的坐标作为约束条件,方程组(5)才有唯一解。另外,由于拉普拉斯坐标不具备旋转不变性,如果直接采用原网格模型的拉普拉斯坐标进行坐标重建,将使网格的局部信息会发生旋转扭曲,特别是对于大尺度变形时,其扭曲尤为严重,如图3所示。
变形前 变形后
图3 拉普拉斯变形时发生特征扭曲现象
也就是说要实现网格模型的保特征变形,不能直接使用原网格的拉普拉斯坐标来重建变形后的网格模型,而应该使用网格曲面变形后各顶点的拉普拉斯坐标。要求网格曲面变形后各顶点的拉普拉斯坐标,按照(4)式的计算方法,应该知道网格曲面变形后的坐标,而网格曲面变形后的坐标正是我们要求解的,所以这又是一个典型的Chicken-and-Egg问题。
我们这里讨论两种解决方案:第一种是我们刚才已经讨论过的迭代方法,我觉得这是解决Chicken-and-Egg问题的一般性方法。如上所述,解决此问题时应首先假定其中一个条件首先得到了满足,这里我们假定变形后的拉普拉斯坐标是知道的,其初值就是网格变形前的拉普拉斯坐标。在操作时,首先直接用原始的Laplace坐标进行预变形,然后根据变形的网格,求解每个顶点的局部旋转变换并对拉普拉斯坐标的方向进行修正,然后进行网格重构。这样经过几次迭代就可以获得满意的效果,但计算量会比较大。
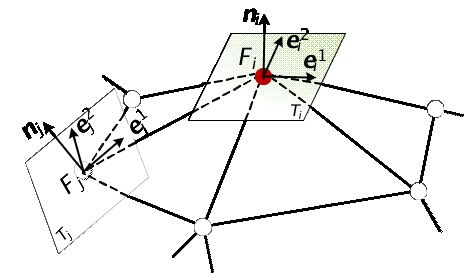
第二种方案,是基于一种旋转不变量的定义来解决的。其实现框架可概括为:首先在网格的每个顶点处建立一个局部坐标系F;其次把每个顶点的拉普拉斯坐标δ表示成局部坐标系F下的相对拉普拉斯坐标δI;然后利用旋转不变量优化方法,求解变换后的局部坐标系F';最后通过δI、F'求取变形后的拉普拉斯坐标δ'。
如图4所示,两相邻顶点上的局部坐标系构建之后,对于Fi、Fj而言,必存在相对变换矩阵Tij,使其满足
![]() ,即
,即![]()
当世界坐标系发生旋转变换时,Fi、Fj也发生相同的旋转变换,然而其相对标架Tij不会发生变化,故称Tij为Fi和Fj之间的旋转不变量。
图4 网格曲面上两相邻顶点上的局部坐标框架
求解变形后的局部坐标框架F',可以归结为求解如下的约束优化问题
顶点vi的拉普拉斯坐标δi用其局部坐标框架可以表示为
δi =λ1ei1+λ2ei2+λ3ni
转换为相对于局部坐标框架下的相对坐标为
δiI=(λ1,λ2,λ3)=(δi·ei1,δi·ei2,δi·ni)
有了变形后的局部坐标框架和相对拉普拉斯坐标,就可以求出变形后的拉普拉斯坐标,最终通过求解一个稀疏线性系统求得变形后网格顶点的坐标。
当然,这方面的应用实例还很多,我只是举几个比较熟悉的例子,其它还有曲线插值计算时,需要知道型值点的参数值,一般曲线可以用弧长参数化,但曲线尚未知,其弧长当然无从算起。可以先用积累弦长参数化方法进行数据参数化,得到初始曲线后,计算其弧长参数,然后迭代计算......
问题在于,除了迭代法之外,还有哪些方法具有普遍性?或通用性?
一些不成熟的想法,分享给大家,欢迎交流讨论!谢绝转载!
华侨大学机电学院:刘斌
参考文献:
1、Flöry S. Fitting curves and surfaces to point clouds in the presence of obstacles[J]. Computer Aided Geometric Design, 2009, 26(2):192-202.
2、Lipman Y, Sorkine O, Cohen-Or D, et al. Differential coordinates for interactive mesh editing[C]//Proc. Shape modeling international.Genova, Italy: IEEE Computer Society, 2004: 181-190.
3、Lipman Y, Sorkine O, Levin D, et al. Linear rotation-invariant coordinates for meshes[J]. ACM Transactions on Graphics, 2005, 24(3): 479-487
4、 黄锦池. 网格曲面上自由形状特征的迁移式设计重用[D].厦门:华侨大学,2015